6.3.3. Removing Edge Capacities

This subsection achieves the opposite of the transformation in Section 6.3.2: It turns all edges in the network into uncapacitated edges. This is useful in some minimum-cost flow algorithms because it ensures that \(G \subseteq G^f\) for any pseudo-flow \(f\) in \(G\): \(f\) cannot saturate any edges in \(G\).

The transformation described here changes the vertex and edge sets of the network but establishes a straightforward relationship between flows in the original network and flows of the same cost in the transformed network. Thus, once again, we can solve the minimum-cost flow problem in the original network by solving it in the transformed network with only uncapacitated edges.

Let \(G\) be an arbitrary flow network. Our goal is to transform \(G\) into an equivalent network \(H\) all of whose edges have infinite capacity. To this end, we introduce a vertex \(z_{x,y}\) for every edge \((x, y)\) in \(G\) such that \(u_{x,y} < \infty\) and replace \((x, y)\) with two edges \(\bigl(x, z_{x,y}\bigr)\) and \(\bigl(y, z_{x, y}\bigr)\). Both edges have infinite capacity. The edge \(\bigl(x, z_{x,y}\bigr)\) has cost \(c_{x,y}\). The edge \((y, z_{x,y})\) has cost zero. Finally, we set \(b_{z_{x,y}} = -u_{x,y}\) and increase \(b_y\) by \(u_{x,y}\). This transformation is illustrated in Figure 6.1.

Figure 6.1

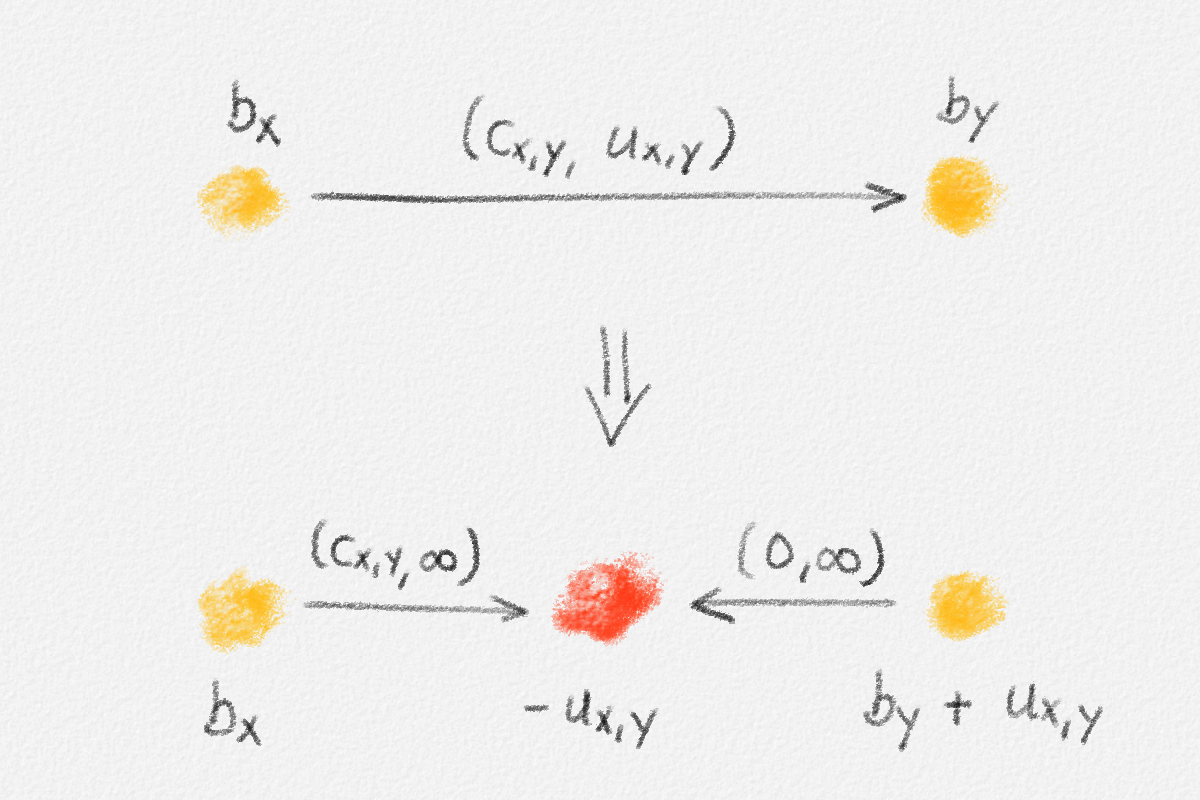
The resulting network \(H\) clearly has no edges of finite capacity. As the next two lemmas show, there exists a simple cost-preserving bijection between flows in \(G\) and flows in \(H\), so a minimum-cost flow in \(G\) can be computed by solving the minimum-cost flow problem in \(H\) instead.

For an arbitrary edge labelling \(f\) of \(G\), let \(f'\) be the corresponding edge labelling of \(H\) defined as

\[f'_{x,y} = \begin{cases} f_{x,y} & \text{if } (x, y) \in G \text{ (and thus $u_{x,y} = \infty$)}\\ f_{x,w} & \text{if } y = z_{x,w}\\ u_{w,x} - f_{w,x} & \text{if } y = z_{w,x}. \end{cases}\tag{6.9}\]

In other words, \(f\) and \(f'\) send the same amount of flow along each uncapacitated edge of \(G\); for each edge \((x, w) \in G\) with capacity \(u_{x,w} < \infty\), \(f'\) sends \(f_{x,w}\) units of flow from \(x\) to \(z_{x, w}\) and \(u_{x,w} - f_{x,w}\) units of flow from \(w\) to \(z_{x, w}\).

Lemma 6.11: \(f\) is a flow in \(G\) if and only if \(f'\) is a flow in \(H\). Both flows have the same cost.

Proof: Throughout this proof, we refer to the vertex supply functions in \(G\) and \(H\) as \(b\) and \(b'\), respectively. The capacity functions in \(G\) and \(H\) are referred to as \(u\) and \(u'\), respectively.

First we show that \(f'\) satisfies the flow conservation constraints if and only if \(f\) does.

For every vertex \(w = z_{x,y}\) in \(H\), we have

\[\sum_{v \in V} \bigl(f'_{w,v} - f'_{v,w}\bigr) = -f'_{x,w} - f'_{y,w} = -f_{x,y} - \bigl(u_{x,y} - f_{x,y}\bigr) = -u_{x,y} = b_w'.\]

Thus, no matter whether \(f\) satisfies the flow conservation constraints, \(f'\) satisfies \(w\)'s flow conservation constraint.

For every vertex \(w \in G\), let \(I_w\) be the set of vertices \(x\) such that the edge \((x,w)\) satisfies \(u_{x,w} < \infty\). Then

\[\begin{aligned} \sum_{x \in H} \bigl(f'_{w,x} - f'_{x,w}\bigr) &= \sum_{x \in V} f_{w,x} + \sum_{x \in I_w}\ \bigl(u_{x,w} - f_{x,w}\bigr) - \sum_{x \in V \setminus I_w} f_{x,w}\\ &= \sum_{x \in V} \bigl(f_{w,x} - f_{x,w}\bigr) + \sum_{x \in I_w} u_{x,w}. \end{aligned}\]

Let

\[\delta_w = \sum_{x \in V}\bigl(f_{w,x} - f_{x,w}\bigr) - b_w.\]

Then

\[\sum_{x \in H} \bigl(f'_{w,x} - f'_{x,w}\bigr) = b_w + \delta_w + \sum_{x \in I_w} u_{x,w} = b'_w + \delta_w.\]

Therefore,

\[\sum_{x \in G'} \bigl(f'_{w,x}- f'_{x,w}\bigr) = b'_w \quad \Leftrightarrow \quad \delta_w = 0 \quad \Leftrightarrow \quad \sum_{x \in V} \bigl(f_{w,x} - f_{x,w}\bigr) = b_w.\]

Thus, \(f\) satisfies the flow conservation constraints in \(G\) if and only if \(f'\) does in \(H\).

Next assume that \(f\) and \(f'\) satisfy the flow conservation constraints in \(G\) and \(H\), respectively. We prove that \(f\) satisfies the capacity constraints in \(G\) if and only if \(f'\) does in \(H\). Consider any edge \((x, y) \in G\).

If \(u_{x,y} = \infty\), then \((x, y) \in H\) and \(f'_{x,y} = f_{x,y}\), and \(u'_{x,y} = \infty\). Thus, \(f_{x,y} \le u_{x,y}\), \(f'_{x,y} \le u'_{x,y}\), and \(f_{x,y} \ge 0\) if and only if \(f'_{x,y} \ge 0\). In other words, \(f\) satisfies the capacity constraint of the edge \((x,y)\) in \(G\) if and only if \(f'\) satisfies the capacity constraint of the edge \((x,y)\) in \(H\).

If \(u_{x,y} < \infty\), then \((x, y) \notin H\) and \(H\) contains two edges \(\bigl(x, z_{x,y}\bigr)\) and \(\bigl(y, z_{x,y}\bigr)\) with \(f'_{x,z_{x,y}} = f_{x,y}\) and \(f'_{y,z_{x,y}} = u_{x,y} - f_{x,y}\). Thus,

\[0 \le f_{x,y} \le u_{x,y} \quad \Leftrightarrow \quad 0 \le f'_{x,z_{x,y}} \text{ and } 0 \le u_{x,y} - f_{x,y} = f'_{y,z_{x,y}}.\]

In other words, \(f\) satisfies the capacity constraint of the edge \((x,y)\) in \(G\) if and only if \(f'\) satisfies the capacity constraints of the two edges \(\bigl(x,z_{x,y}\bigr)\) and \(\bigl(y,z_{x,y}\bigr)\) in \(H\).

Since \(f\) satisfies both the capacity and flow conservation constraints in \(G\) if and only if \(f'\) does in \(H\), this shows that \(f\) is a flow in \(G\) if and only if \(f'\) is a flow in \(H\).

To determine the cost of \(f'\), we can divide the edges of \(H\) into two groups: For every edge \((x,y) \in G\) with \(u_{x,y} = \infty\), \(H\) also contains the edge \((x,y)\) and we have \(f'_{x,y} = f_{x,y}\) and \(c'_{x,y} = c_{x,y}\). For every edge \((x,y) \in G\) with \(u_{x,y} < \infty\), \(H\) contains the edge \(\bigl(x, z_{x,y}\bigr)\) and once again, \(f'_{x, z_{x,y}} = f_{x,y}\) and \(c'_{x, z_{x,y}} = c_{x,y}\). These are the edges in the first group \(E_1'\). We have

\[\sum_{e \in G} c_ef_e = \sum_{e \in E_1'}c'_ef'_e.\]

The second group \(E_2'\) contains all remaining edges of \(H\). Any such edge \((x,y) \in E_2'\) satisfies \(y = z_{w,x}\) for some edge \((w,x) \in G\) with \(u_{w,x} < \infty\). Thus, \(c'_{x,y} = 0\) and

\[\sum_{e \in E_2'}c'_ef'_e = 0.\]

Together, these two equalities imply that

\[\sum_{e \in H} c'_ef'_e = \sum_{e \in E_1'} c'_ef'_e + \sum_{e \in E_2'} c'_ef'_e = \sum_{e \in G} c_ef_e,\]

that is, \(f\) and \(f'\) have the same cost. ▨

By Lemma 6.11, every flow \(f\) in \(G\) has a corresponding flow \(f'\) in \(H\) of the same cost, defined by (6.9). The following observation shows that every flow \(f'\) in \(H\) corresponds to a flow in \(f\) via (6.9). Since this mapping has an obvious inverse, it is thus a bijection between flows in \(G\) and flows in \(H\). Since each flow \(f\) in \(G\) has the same cost as its corresponding flow in \(H\), it is thus also a bijection between minimum-cost flows in \(G\) and \(H\).

Observation 6.12: For every flow \(f'\) in \(H\), there exists a flow \(f\) in \(G\) such that \(f'\) is obtained from \(f\) via (6.9).

Proof: Let \(f\) be defined as

\[f_{x,y} = \begin{cases} f'_{x,y} & \text{if } u_{x,y} = \infty\\ f'_{x,z_{x,y}} & \text{if } u_{x,y} < \infty, \end{cases}\]

and let \(f''\) be the edge labelling obtained from \(f\) via (6.9). If \(u_{x,y} = \infty\), then \(f''_{x,y} = f_{x,y} = f'_{x,y}\). If \(u_{x,y} < \infty\), then \(f''_{x,z_{x,y}} = f_{x,y} = f'_{x,z_{x,y}}\) and \(f''_{y,z_{x,y}} = u_{x,y} - f_{x,y}\). Since \(f'\) satisfies flow conservation at \(z_{x,y}\), we have

\[\begin{aligned} f'_{x,z_{x,y}} + f'_{y,z_{x,y}} &= -b_{z_{x,y}}\\ f_{x,y} + f'_{y,z_{x,y}} &= u_{x,y}\\ f'_{y,z_{x,y}} &= u_{x,y} - f_{x,y} = f''_{y,z_{x,y}}. \end{aligned}\]

Thus, \(f' = f''\). By Lemma 6.11, \(f\) is a flow in \(G\) since \(f'\) is a flow in \(H\). ▨

Note that, if \(G\) has \(n\) vertices and \(m\) edges, then \(H\) has at most \(n + m\) vertices and at most \(2m\) edges. Some of the algorithms discussed in this section repeatedly compute shortest paths in a residual network, using Dijkstra's algorithm. On \(G\), this would take \(O(n \lg n + m)\) time. On \(H\), it seems to take \(O((n + m) \lg n + m) = O(m \lg n)\) time, which can be worse by a \(\lg n\) factor if \(G\) is sufficiently dense. The following exercise asks you to show that the single-source shortest paths problem in \(H\) can in fact be solved in \(O(n \lg n + m)\) time:

Exercise 6.3: Consider a graph \(G = (U \cup W, E)\) whose vertex set can be divided into two subsets \(U\) and \(W\) such that every vertex in \(W\) has exactly two neighbours, both of which are in \(U\), while the vertices in \(U\) may have an arbitrary number of neighbours, and these neighbours may be in \(U\) or \(W\). Let \(n_U = |U|\) and \(m = |E|\). Prove that the single-source shortest paths problem in \(G\) can be solved in \(O(n_U \lg n_U + m)\) time.