7.3.3. Minimum-Weight Perfect Matching

The reduction of the minimum-weight perfect matching problem to a minimum-cost flow problem is similar to the reduction of the maximum-weight matching problem to a minimum-cost flow problem:

Lemma 7.7: It takes \(O\bigl(n^2 \sqrt{m}\bigr)\) time to decide whether a bipartite graph has a perfect matching. If such a matching exists, a minimum-weight perfect matching can be found in \(O\bigl(n^2 \lg n + nm\bigr)\) time.

Proof: If \(|U| \ne |W|\), the algorithm can terminate immediately because no perfect matching exists. If \(|U| = |W| = n\), a perfect matching is any matching of size \(n\), and there exists no larger matching. Thus, we find a maximum-cardinality matching in \(O(n^2\sqrt{m})\) time, using Corollary 7.4, and then compare the size of the computed matching to \(n\). If the matching has size \(n\), it is a perfect matching. Otherwise, there is no perfect matching.

If there exists a perfect matching, we are now interested in finding a matching of size \(n\) whose cost is minimized. This can be done in almost the same way as in Corollary 7.6. We construct the network \(\vec{G}\) as in the maximum-weight matching problem but (a) do not add the edge \((s,t)\) and (b) choose the cost of every edge \((u,w)\) with \(u \in U\) and \(w \in W\) to be equal to its cost in \(G\). Then it is easy to verify that every flow in \(\vec{G}\) sends one unit of flow along exactly one of the out-edges of every vertex in \(U\) and along exactly one in-edge of every vertex in \(W\). Thus, it corresponds to a perfect matching. Since we minimize the cost of the flow, the computed matching has minimum cost among all perfect matchings.

In fact, the addition of the two vertices \(s\) and \(t\) when computing a maximum-weight matching was necessary only because we did not know the cardinality of a maximum-weight matching. Thus, we (a) did not know which vertices in \(U\) have any incident edges in the computed matching and (b) needed a way to divert flow from \(s\) to \(t\) via the edge \((s,t)\) if this gives us the cheapest flow. In the minimum-weight perfect matching problem, we send exactly one unit of flow from every vertex \(u \in U\) to some vertex \(w \in W\) and every vertex \(w \in W\) receives exactly one unit of flow from some vertex \(u \in U\). Thus, we can simplify \(\vec{G}\) by removing \(s\), \(t\), and their incident edges and instead setting \(b_u = 1\) for every vertex \(u \in U\) and \(b_w = -1\) for every vertex \(w \in W\). This is illustrated in Figure 7.8 and has the benefit that the maximum capacity and the maximum absolute node supply are now \(1\), so the successive shortest paths algorithm is faster than the enhanced capacity scaling algorithm; its running time is \(O\bigl(n^2 \lg n + nm\bigl)\) if \(U = 1\) while the enhanced capacity scaling algorithm takes \(O((n \lg n + m) m \lg n)\) time. ▨

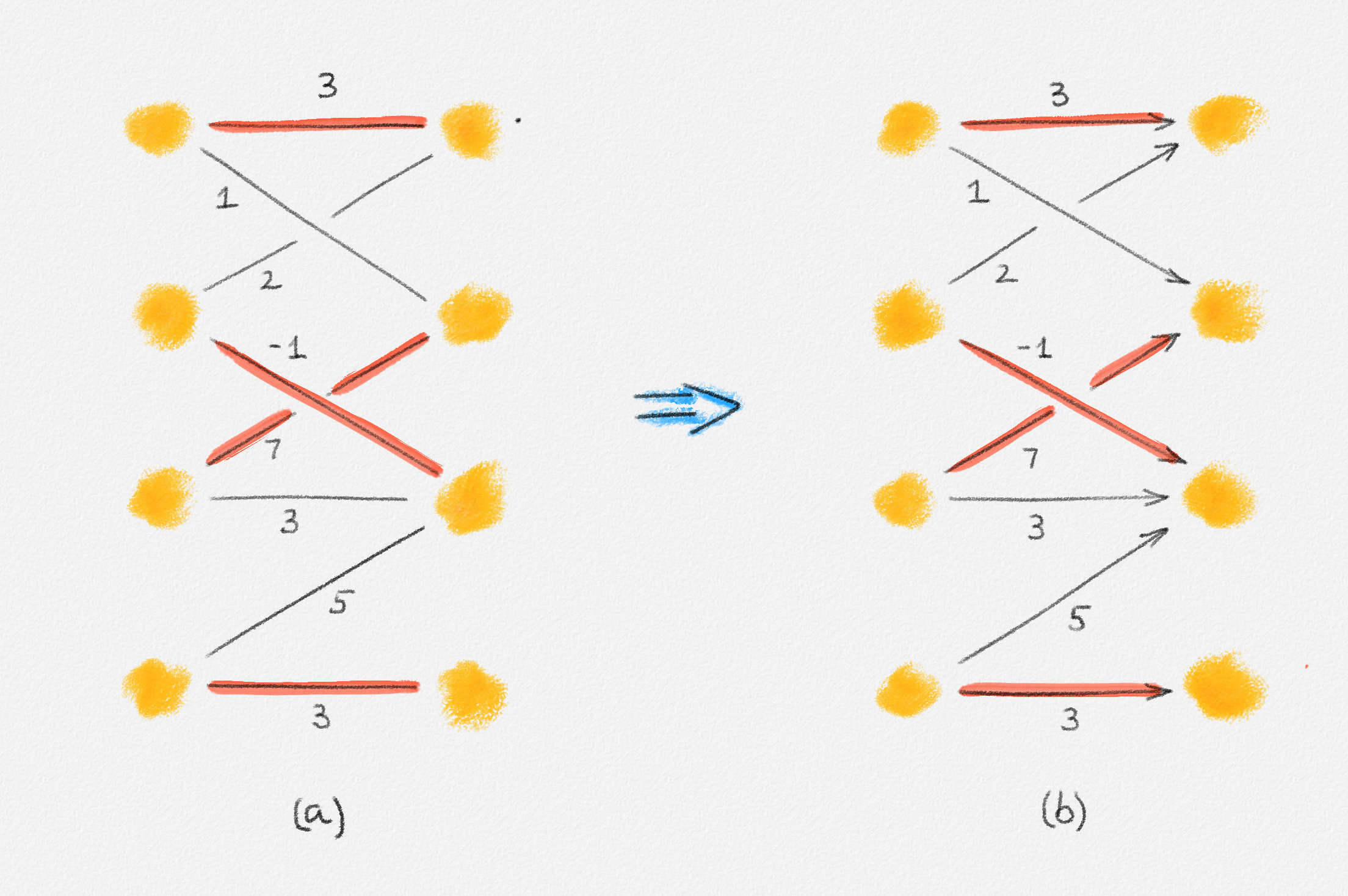
Figure 7.8: (a) A bipartite graph \(G\) and a minimum-weight perfect matching of \(G\) shown in red. The edge labels are edge costs. (b) The graph \(\vec{G}\) obtained from \(G\) by directing all edges of \(G\) from left to right. Edge costs are not negated in this construction, and no verices or edges are added. All edges have capacity \(1\) (not shown). Every vertex in \(U\) has supply balance \(1\). Every vertex in \(W\) has supply balance \(-1\). Vertex supply balances are not shown. The minimum-cost flow corresponding to the minimum-weight perfect matching in (a) sends one unit of flow along each of the red edges.

We will soon discuss a reduction of the maximum-weight matching problem in a graph \(G\) with \(n\) vertices and \(m\) edges to the minimum-weight perfect matching problem in a graph \(G'\) with \(2n\) vertices and \(2m + n\) edges. If \(G\) is bipartite, then so is \(G'\). Thus, we can in fact find a maximum-weight matching in \(O\bigl(n^2 \lg n + nm\bigr)\) time using the successive shortest paths algorithm, an improvement over the bound proven in Corollary 7.6.