7.3.2. Maximum-Weight Matching

Finding a maximum-weight matching via network flows is a little harder than finding a maximum-cardinality matching because we cannot easily reduce it to finding a maximum flow; we need to find a minimum-cost flow instead. Once again, we turn the bipartite graph \(G = (U, W, E)\) into a directed network \(\vec{G}\) as in the previous subsection. Again, every edge has capacity \(1\). The cost of every edge incident to \(s\) or \(t\) is \(0\). The cost of every edge \((u, w)\) with \(u \in U\) and \(w \in W\) is the negation of this edge's cost in \(G\). Finally, we add an uncapacitated edge \((s, t)\) of cost zero to \(\vec{G}\). The supply balance of every vertex in \(U \cup W\) is \(0\), \(b_s = |U|\), and \(b_t = -|U|\). This construction is shown in Figure 7.7.

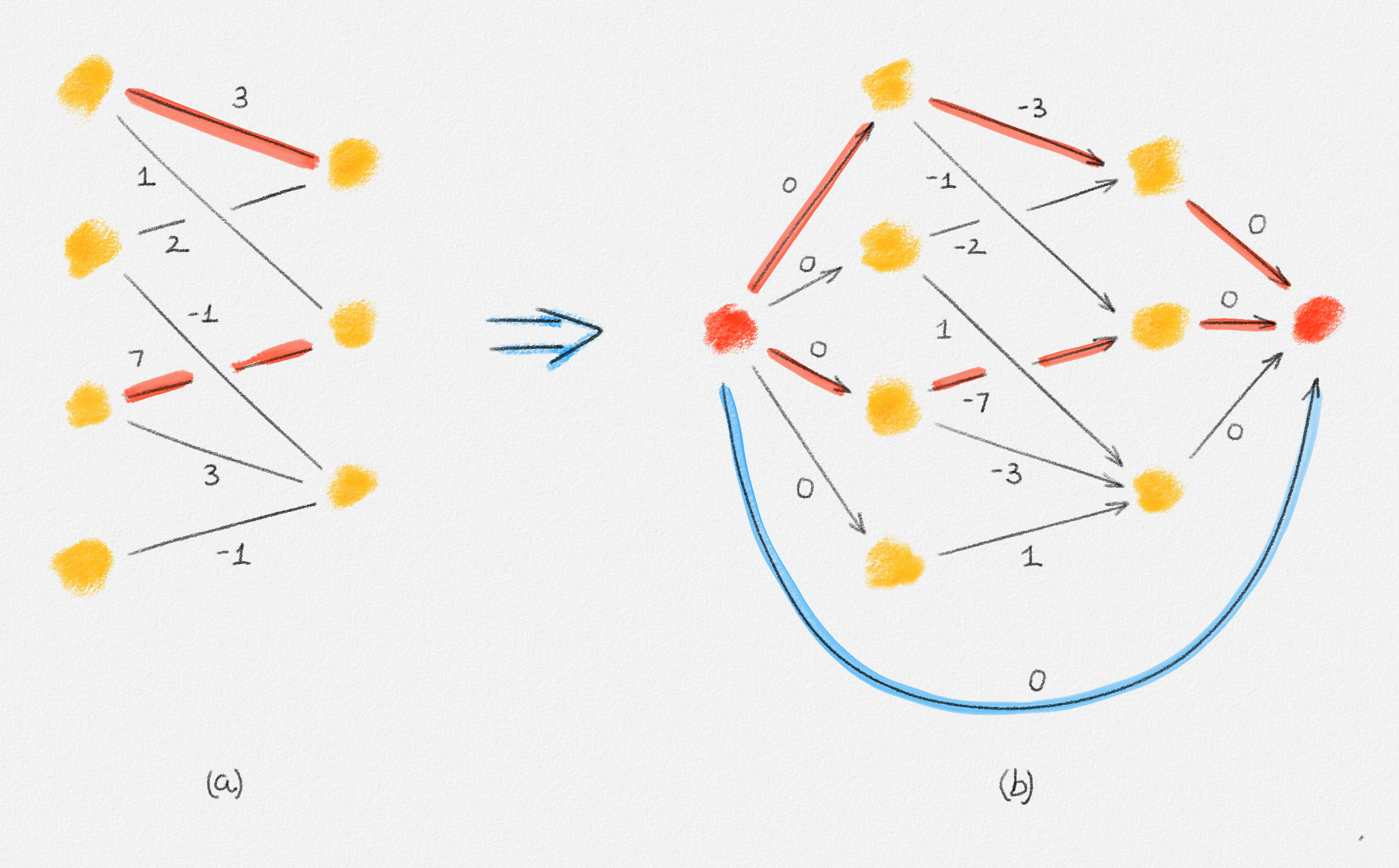
Figure 7.7: (a) A bipartite graph \(G\) and a maximum-weight matching of \(G\) shown in red. The edge labels are edge costs. (b) The graph \(\vec{G}\) obtained from \(G\) by adding two vertices \(s\) and \(t\), directing all edges of \(G\) from left to right, making all vertices in \(U\) out-neighbours of \(s\), making all vertices in \(W\) in-neighbours of \(t\), and adding an edge from \(s\) to \(t\). All edges incident to \(s\) or \(t\) have cost \(0\). The cost of any other edge is the negation of the cost of its corresponding edge in \(G\). All edges except the edge \((s, t)\) have capacity \(1\). The edge \((s, t)\) is uncapacitated. Edge capacities are not shown. Vertex supply balances are not shown. \(s\) has supply balance \(|U| = 4\). \(t\) has supply balance \(-|U| = -4\). All other supply balances are \(0\). The minimum-cost flow corresponding to the maximum-weight matching in (a) is shown in red and blue. One unit of flow is sent along each of the red \(st\)-paths. The remainder of the flow, \(2\) units of flow, is sent from \(s\) to \(t\) along the blue edge, at cost \(0\).

Lemma 7.5: \(M\) is a matching in \(G\) if and only if there exists an integral flow \(f\) in \(\vec{G}\) such that \(M = \{e \in G \mid f_e = 1\}\). The cost of \(M\) is the negation of the cost of \(f\).

Proof: The proof that \(M\) is a matching in \(G\) if and only if there exists an integral flow \(f\) in \(\vec{G}\) such that \(M = \{e \in G \mid f_e = 1\}\) is analogous to the proof of Lemma 7.3. We only need to observe that \(|U|\) is the maximum cardinality of any matching in \(G\) and that any amount of flow not sent from \(s\) to \(t\) via a path that includes a vertex in \(U\) and a vertex in \(W\) can be sent via the uncapacitated edge \((s,t)\).

To see that the cost of \(M\) is the negation of the cost of \(f\), observe that every edge in \(\vec{G}\) has cost \(0\), except edges \((u,w)\) with \(u \in U\) and \(w \in W\). For any such edge \(e\), its cost in \(\vec{G}\) is the negation of its cost in \(G\). Since \(e \in M\) if and only if \(f_e = 1\), this shows that \(M\)'s cost is the negation of the cost of \(f\). ▨

Corollary 7.6: A maximum-weight matching of a bipartite graph \(G\) can be found in \(O((n \lg n + m)m \lg n)\) time.

Proof: Constructing \(\vec{G}\) from \(G\) takes \(O(n + m)\) time. By Theorem 6.75, we can find a minimum-cost flow \(f\) in \(\vec{G}\) in \(O((n \lg n + m)m \lg n)\) time. As observed in Section 5.3, this flow is integral. Thus, by Lemma 7.5, the set \(M = \{e \in G \mid f_e = 1\}\) is a matching in \(G\). Constructing \(M\) from \(f\) takes \(O(n + m)\) time. Therefore, the whole procedure for computing \(M\) takes \(O((n \lg n + m)m \lg n)\) time.

Next assume that \(M\) is not a maximum-weight matching. Then there exists a matching \(M'\) of greater cost. By Lemma 7.5, \(M' = \{e \in G \mid f'_e = 1\}\) for some integral flow \(f'\) in \(\vec{G}\). Moreover, the cost of \(f'\) is the negation of the cost of \(M'\). Since the same is true for \(f\) and \(M\), this implies that \(f'\) has a lower cost than \(f\), a contradiction because \(f\) is a minimum-cost flow. This proves that \(M\) is a maximum-weight matching. ▨