5.1.3. Dinitz's Algorithm*

What prevents the Edmonds-Karp algorithm from achieving a better running time is that it constructs \(G^f\) and uses a full BFS of \(G^f\) to find the augmenting path in each iteration. Dinitz's algorithm follows the same basic idea of increasing the current flow by pushing more flow along augmenting paths, but it uses a single BFS to find potentially many augmenting paths. As we will see, this reduces its running time to \(O\bigl(n^2m\bigr)\).

Running BFS in \(G^f\) labels every vertex \(x\) in \(G^f\) with its distance \(\mathrm{dist}_{G^f}(s,x)\).

The level graph \(L^f \subseteq G^f\) (see Figure 5.13) is obtained from \(G^f\) by deleting all edges \((x,y)\) such that \(\mathrm{dist}_{G^f}(s,y) \le \mathrm{dist}_{G^f}(s,x)\).

It is easy to see that \(\mathrm{dist}_{G^f}(s,x) = \mathrm{dist}_{L^f}(s,x)\) for all \(x \in V\). This distance is called the level of \(x\) in \(G^f\).

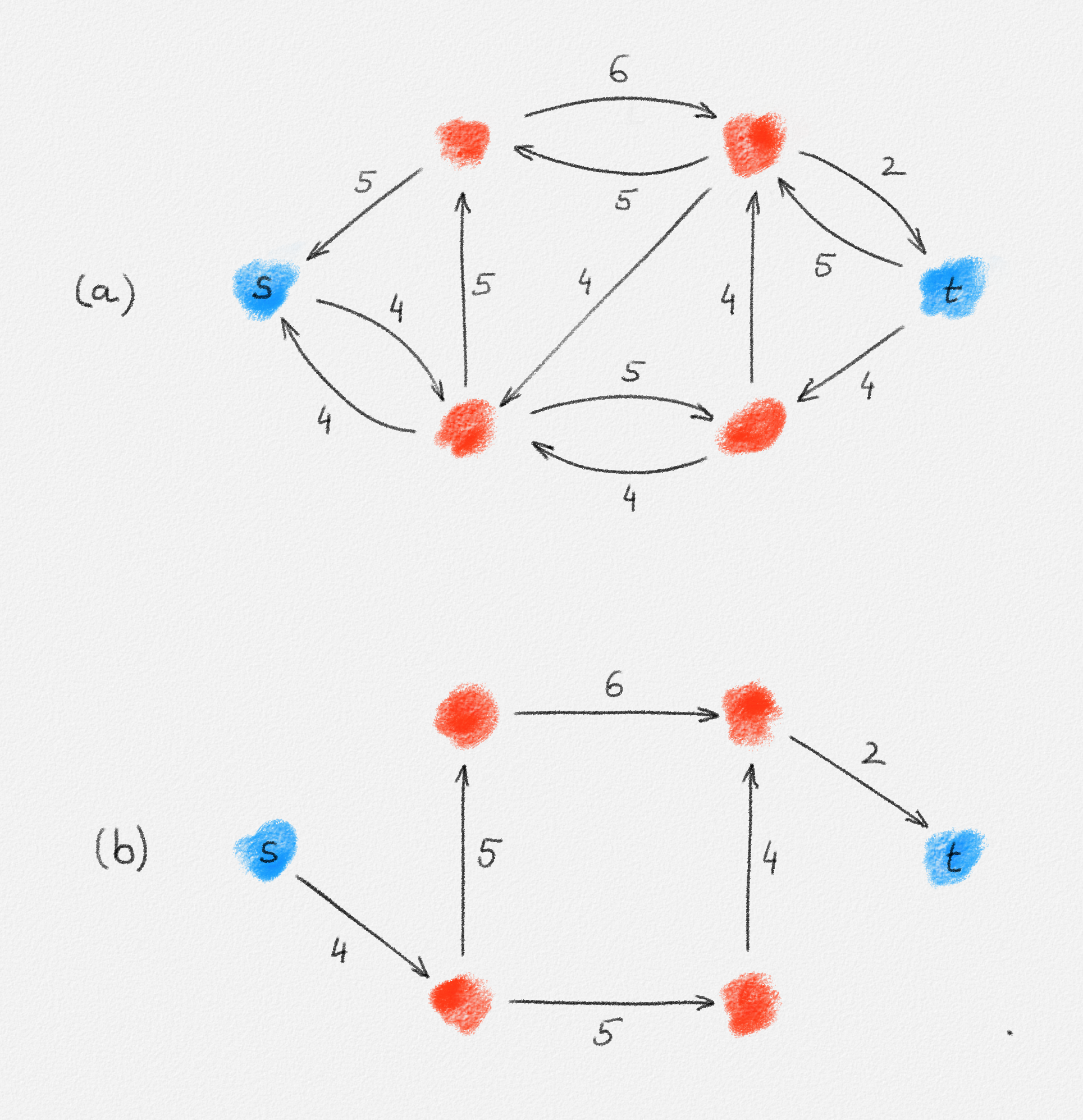
Figure 5.13: (a) A residual network. (b) The corresponding level graph.

Let \(\ell^f\) be \(t\)'s level in \(G^f\). The idea of Dinitz's algorithm is to spend \(O(nm)\) time to find a new \(st\)-flow \(f'\) with \(\ell^{f'} > \ell^f\) in each iteration. As long as there exists an augmenting path from \(s\) to \(t\) in the current residual network \(G^f\), \(\ell^f \le n\). Thus, the algorithm runs for at most \(n\) iterations, each with cost \(O(nm)\), giving a running time of \(O\bigl(n^2 m\bigr)\), which is better than \(O\bigl(nm^2\bigr)\) unless \(G\) is sparse. An illustration of Dinitz's algorithm is given in Figure 5.15.

Let \(b\) be a feasible \(st\)-flow in \(L^f\). Any such flow \(b\) defines a new \(st\)-flow \(f'\) in \(G\) as

\[f'_{x,y} = \begin{cases} f_{x,y} - \min\bigl(b_{y,x},f_{x,y}\bigr) & \text{if } (y,x) \in L^f\\ f_{x,y} + \max\bigl(0,b_{x,y} - f_{y,x}\bigr) & \text{if } (x,y) \in L^f\\ f_{x,y} & \text{otherwise.} \end{cases}\tag{5.8}\]

The next lemma shows that \(f'\) is once again a feasible \(st\)-flow in \(G\).

Lemma 5.7: If \(f\) is a feasible \(st\)-flow in \(G\) and \(b\) is a feasible \(st\)-flow in \(L^f\), then the flow \(f'\) defined in (5.8) is also a feasible \(st\)-flow in \(G\).

Proof: The proof is very similar to the proof of Lemma 5.1. Let \(f^\delta = f' - f\). Then

\[f^\delta_{x, y} = \begin{cases} \max\bigl(0, b_{x, y} - f_{y, x}\bigr) & \text{if } (x, y) \in L^f\\ -\min\bigl(b_{y, x}, f_{x, y}\bigr) & \text{if } (y, x) \in L^f\\ 0 & \text{otherwise.} \end{cases}\]

If \((x, y) \in L^f\), this implies that

\[\begin{aligned} f^\delta_{x, y} - f^\delta_{y, x} &= \max\bigl(0, b_{x, y} - f_{y, x}\bigr) + \min\bigl(b_{x, y}, f_{y, x}\bigr)\\ &= b_{x, y}\\ &= b_{x, y} - b_{y, x} \end{aligned}\]

because \(b_{y, x} = 0\). If both \((x, y), (y, x) \notin L^f\), then

\[f^\delta_{x, y} = f^\delta_{y, x} = b_{x, y} = b_{y, x} = 0,\]

so once again

\[f^\delta_{x, y} - f^\delta_{y, x} = b_{x, y} - b_{y, x}.\]

Thus,

\[\begin{aligned} \sum_{y \in V} \bigl(f'_{x, y} - f'_{y, x}\bigr) &= \sum_{y \in V} \bigl(f_{x, y} - f_{y, x}\bigr) + \sum_{y \in V} \Bigl(f^\delta_{x, y} - f^\delta_{y, x}\Bigr)\\ &= \sum_{y \in V} \bigl(f_{x, y} - f_{y, x}\bigr) + \sum_{y \in V} \bigl(b_{x, y} - b_{y, x}\bigr) = 0 \quad \forall x \in V \setminus \{s, t\} \end{aligned}\]

because both \(f\) and \(b\) are feasible \(st\)-flows. This shows that \(f'\) satisfies flow conservation.

To prove that \(f'\) satisfies the capacity constraints, consider any pair of vertices \((x,y)\).

If \((x,y) \notin L^f\) and \((y,x) \notin L^f\), then

\[0 \le f'_{x,y} = f_{x,y} \le u_{x,y}\]

because \(f\) is a feasible flow.

If \((x,y) \in L^f\), then

\[0 \le f_{y,x} - \min\bigl(b_{x,y}, f_{y,x}\bigr) \le f_{y,x} \le u_{y,x}\]

and

\[\begin{aligned} 0 &\le f_{x,y} \le f_{x,y} + \max\bigl(0, b_{x,y} - f_{y,x}\bigr)\\ &\le \max\left(f_{x,y}, f_{x,y} + u^f_{x,y} - f_{y,x}\right)\\ &= \max\bigl(f_{x,y}, f_{x,y} + u_{x,y} - f_{x,y} + f_{y,x} - f_{y,x}\bigr)\\ &= \max\bigl(f_{x,y}, u_{x,y}\bigr)\\ &= u_{x,y} \end{aligned}\]

because \(f\) and \(b\) are feasible \(st\)-flows in \(G\) and \(L^f\), respectively. Since \(f'_{x,y} = f_{x,y} + \max\bigl(0, b_{x,y} - f_{y,x}\bigr)\) and \(f'_{y,x} = f_{y,x} - \min\bigl(b_{x,y}, f_{y,x}\bigr)\), this shows that \(0 \le f'_{x,y} \le u_{x,y}\) and \(0 \le f'_{y,x} \le u_{y,x}\). Thus, \(f'\) satisfies the capacity constraints. Since it also satisfies flow conservation, it is a feasible \(st\)-flow. ▨

The key to guaranteeing that Dinitz's algorithm terminates after at most \(n\) iterations is to find the right kind of flow in \(L^f\), one that ensures that \(\ell^{f'} > \ell^f\). Next we define such a flow and show how to find it efficiently.