2.2.2. Properties of Shortest Paths

The LP formulation of the SSSP problem is based on the following two properties of distances from \(s\).

Lemma 2.1: Let \(v \ne s\) and let \(u\) be \(v\)'s predecessor in \(\Pi_{G,w}(s,v)\). Then the subpath \(P\) of \(\Pi_{G,w}(s,v)\) from \(s\) to \(u\) is a shortest path from \(s\) to \(u\).

Proof: Since \(P\) is a path from \(s\) to \(u\), we have

\[w(P) \ge \mathrm{dist}_{G,w}(s,u).\]

If \(w(P) > \mathrm{dist}_{G,w}(s,u)\), then the path \(\Pi_{G,w}(s,u) \circ \langle (u,v) \rangle\) (the concatenation of the path \(\Pi_{G,w}(s,u)\) with the single-edge path \(\langle (u,v) \rangle\)) is a path from \(s\) to \(v\) of length

\[\mathrm{dist}_{G,w}(s,u) + w_{u,v} < w(P) + w_{u,v} = \mathrm{dist}_{G,w}(s,v),\]

a contradiction. This is illustrated in Figure 2.4. ▨

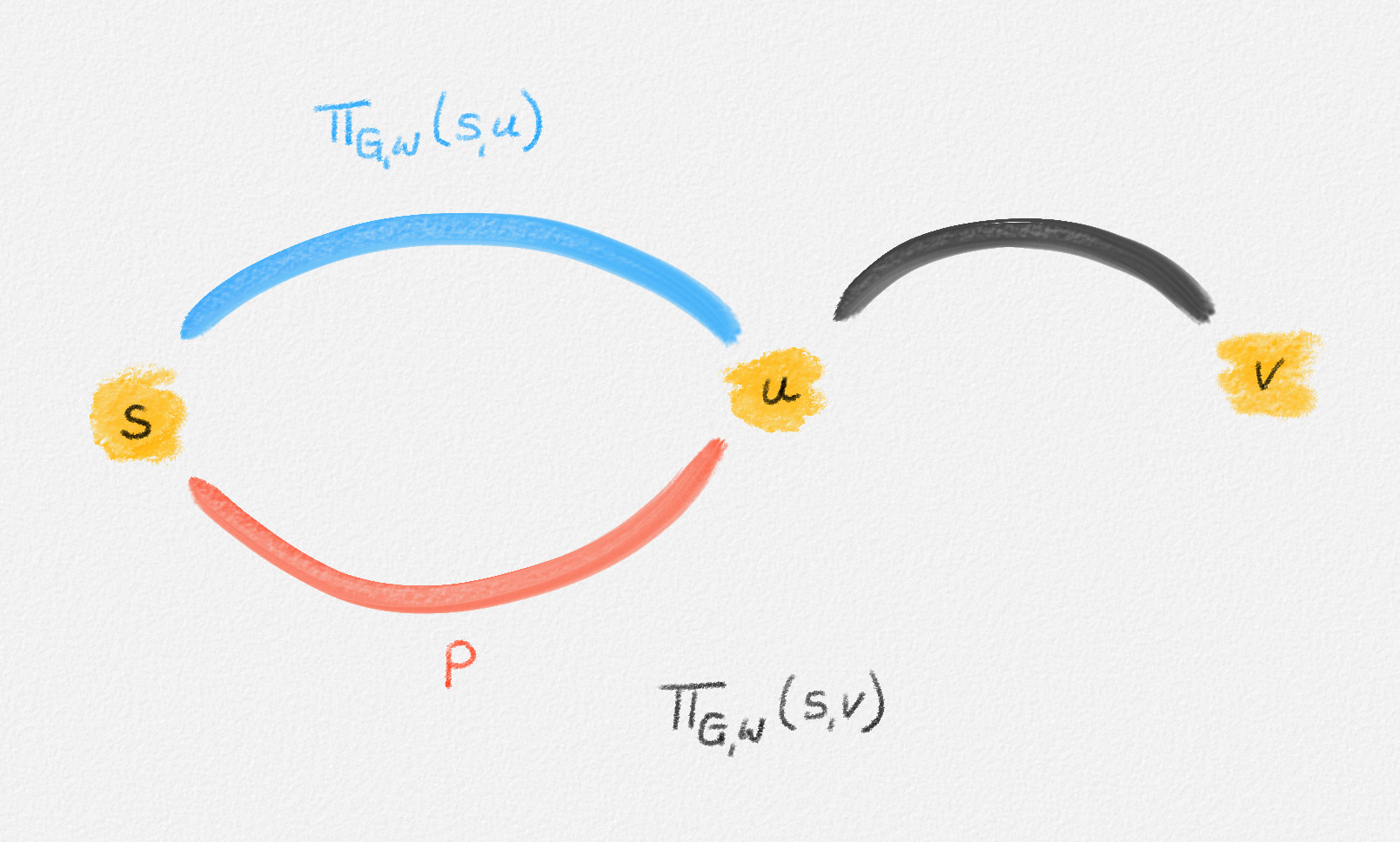
Figure 2.4: If \(\Pi_{G,w}(s,u)\) is shorter than \(P\), then \(\Pi_{G,w}(s,v)\) cannot be a shortest path.

Lemma 2.2:

\[\begin{multline} \mathrm{dist}_{G,w}(s,v) =\\ \begin{cases} 0 & \text{if } v = s\\ \min \{ \mathrm{dist}_{G,w}(s,u) + w_{u,v} \mid (u,v) \in E \} & \text{if } v \ne s \end{cases}\phantom{spc} \end{multline}\tag{2.2}\]

Proof: The case when \(v = s\) is obvious since the shortest path from \(s\) to \(s\) contains only \(s\) and thus has length \(0\). (Convince yourself that this follows from the absence of negative cycles.)

For \(v \ne s\), let \(z\) be \(v\)'s predecessor in \(\Pi_{G,w}(s,v)\). By Lemma 2.1,

\[\begin{aligned} \mathrm{dist}_{G,w}(s,v) &= \mathrm{dist}_{G,w}(s,z) + w_{z,v}\\ &\ge \min \{ \mathrm{dist}_{G,w}(s,u) + w_{u,v} \mid (u,v) \in E \}. \end{aligned}\tag{2.3}\]

Conversely, if \(z'\) is \(v\)'s in-neighbour that minimizes \(\mathrm{dist}_{G,w}(s,z') + w_{z',v}\), then \(\Pi_{G,w}(s, z') \circ \langle (z',v) \rangle\) is a path from \(s\) to \(v\) of length

\[\mathrm{dist}_{G,w}(s,z') + w_{z',v} = \min \{ \mathrm{dist}_{G,w}(s,u) + w_{u,v} \mid (u,v) \in E \}.\]

Thus,

\[\mathrm{dist}_{G,w}(s,v) \le \min \{ \mathrm{dist}_{G,w}(s,u) + w_{u,v} \mid (u,v) \in E \}.\tag{2.4}\]

Equation (2.2) follows from inequalities (2.3) and (2.4). ▨