7.6.2. Maximum-Weight Matching

To compute a maximum-weight matching in a bipartite graph \(G\), we first observe that this is the same as computing a minimum-weight matching in \(G\) after negating all edge weights. To compute a minimum-weight matching in \(G\), we reduce this problem to computing a minimum-weight perfect matching in an auxiliary graph \(G''\).

The graph \(G''\) consists of \(G\) and an identical copy \(G'\) of \(G\). In addition, for every vertex \(x \in G\), \(G''\) has an edge \((x,x')\) of weight zero, where \(x'\) is the copy of \(x\) in \(G'\). This is illustrated in Figure 7.16. \(G''\) has a trivial perfect matching \(\{(x,x') \mid x \in G\}\). Since \(G''\) has \(2n\) vertices and \(2m + n\) edges, we can compute a minimum-weight perfect matching \(M''\) of \(G''\) in \(O\bigl(n^2 \lg n + nm\bigr)\) time. By the next lemma, the matching \(M = \{(x,y) \in M'' \mid x,y \in G\}\) is a minimum-weight matching of \(G\).

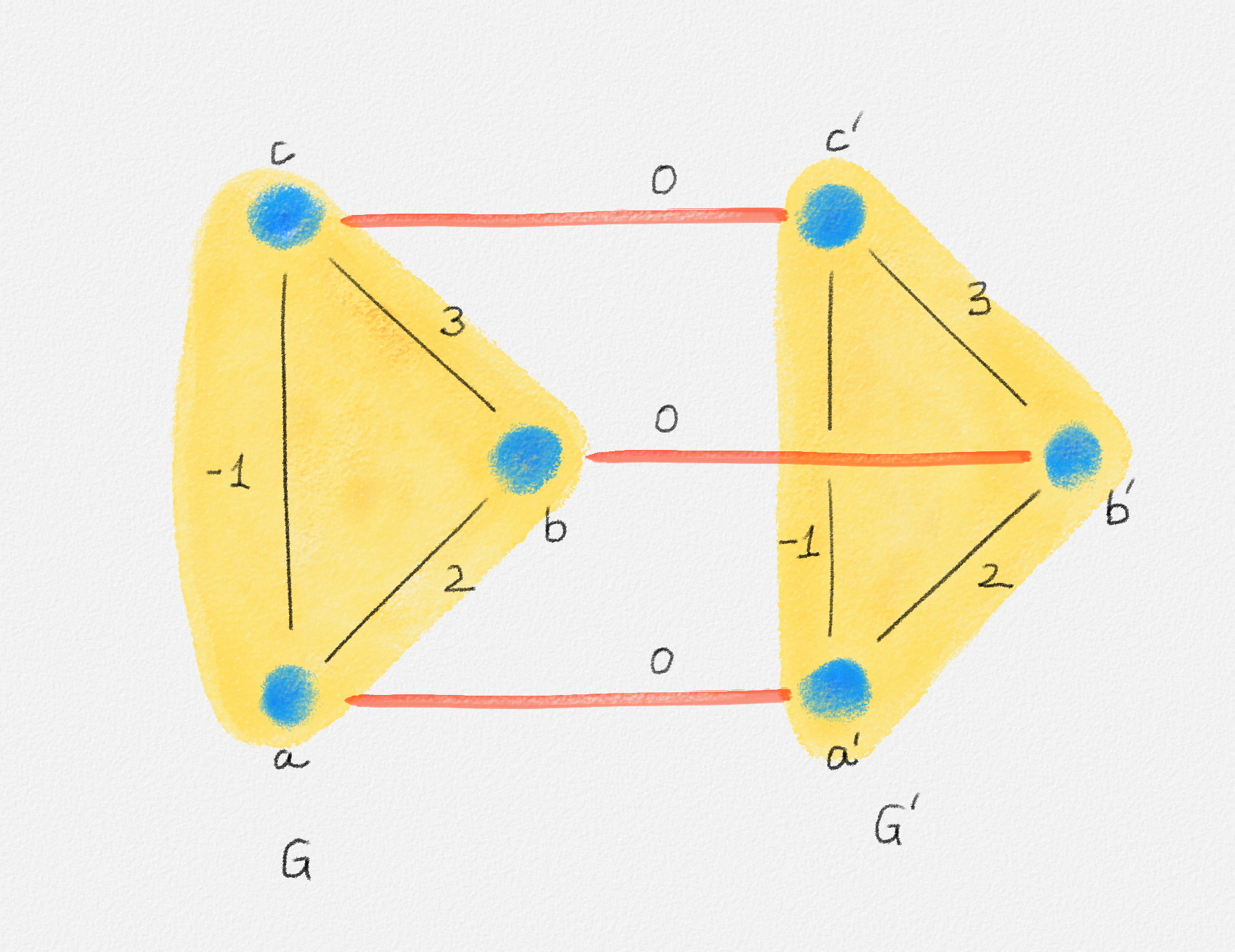
Figure 7.16: The graph \(G''\) used to compute a minimum-weight matching in \(G\). \(G\) and its copy, \(G'\), are shaded. Note that every edge in \(G'\) has the same cost as the corresponding edge in \(G\). The edge between every vertex in \(G\) and its copy in \(G'\) has cost \(0\). By connecting each vertex in \(G\) to its copy in \(G'\), we obtain a trivial perfect matching of \(G''\).

Lemma 7.28: If \(M''\) is a minimum-weight perfect matching of \(G''\), then the matching \(M = \{(x,y) \in M'' \mid x,y \in G\}\) is a minimum-weight matching of \(G\).

Proof: Let \(M^*\) be a minimum-weight matching of \(G\) and consider the two matchings \(M = \{(x, y) \in M'' \mid x, y \in G\}\) and \(M' = \{(x,y) \in M'' \mid x, y \in G'\}\). Since \(M^*\) is a minimum-weight matching of \(G\), \(M\) is a matching of \(G\), and \(M'\) is a matching of \(G'\), we have \(c(M) \ge c(M^*)\) and \(c(M') \ge c(M^*)\). If \(c(M) > c(M^*)\), then observe that \(c(M'') = c(M) + c(M') > 2c(M^*)\) because every edge between \(G\) and \(G'\) in \(G''\) has weight \(0\). On the other hand, the matching \(M''' = \{(x,y), (x',y') \mid (x,y) \in M^*\} \cup \{(x,x') \mid x \in G \text{ is unmatched by } M^*\}\) is a perfect matching of \(G''\) of weight \(2c(M^*)\). Thus, \(M''\) is not a minimum-weight perfect matching of \(G''\), a contradiction. This shows that \(c(M) \le c(M^*)\). Since \(c(M) \ge c(M^*)\), we therefore have \(c(M) = c(M^*)\), that is, \(M\) is a minimum-weight matching of \(G\). ▨

Note that the reduction from the maximum-weight matching problem to the minimum-weight perfect matching problem discussed in this section works for any graph, not just for bipartite graphs. In order to compute a maximum-weight matching, however, we need an algorithm for computing a minimum-weight perfect matching. We only discussed how to do this for bipartite graphs, so we obtain the following result using Theorem 7.27 and Lemma 7.28:

Theorem 7.29: A maximum-weight matching in a bipartite graph can be computed in \(O\bigl(n^2 \lg n + nm\bigr)\) time.