7.7.1.2. Expanding Blossoms

It remains to show that if \(B\) is a blossom in \(G\), then \(M\) is a maximum-cardinality matching of \(G\) if and only if \(M/B\) is a maximum-cardinality matching of \(G/B\), and that an augmenting path for \(M\) in \(G\) can be constructed in linear time from an augmenting path for \(M/B\) in \(G/B\) if \(M\) and \(M/B\) are not maximum-cardinality matchings.

We start with the second claim, which immediately implies half of the first claim: If \(M/B\) is not a maximum-cardinality matching, then \(M\) is not a maximum-cardinality matching, as witnessed by the augmenting path for \(M\) that we are able to construct.

Lemma 7.33: Let \(B\) be a blossom in \(G\). Then an augmenting path \(P\) for \(M\) in \(G\) can be constructed from an augmenting path \(P'\) for \(M/B\) in \(G/B\) in \(O(m)\) time.

Proof: Consider an augmenting path \(P'\) in \(G/B\) with endpoints \(x\) and \(y\). If this path does not include \(v_B\), then all its edges are edges of \(G\) and are matched by \(M\) if and only if they are matched by \(M/B\); its endpoints are unmatched by \(M\). Thus, it is an augmenting path in \(G\). See Figure 7.22.

Figure 7.22: If an augmenting path \(P'\) for \(M/B\) in \(G/B\) does not include \(v_B\), then it is also an augmenting path for \(M\) in \(G\) that does not interact with \(B\).

If \(P'\) includes \(v_B\), then one of the edges incident to \(v_B\) is unmatched. Let us call this edge \((v_B,w)\) and assume that this is the first edge on the subpath of \(P'\) from \(v_B\) to \(y\). See Figure 7.23. Then there exists a vertex \(v \in B\) such that \((v,w)\) is an unmatched edge of \(G\). Let \(P'_w\) be the subpath of \(P'\) from \(w\) to \(y\). \(P'_w\) is an alternating path in \(G\). Since \((v_B,w)\) is unmatched, the first edge in \(P'_w\) is matched.

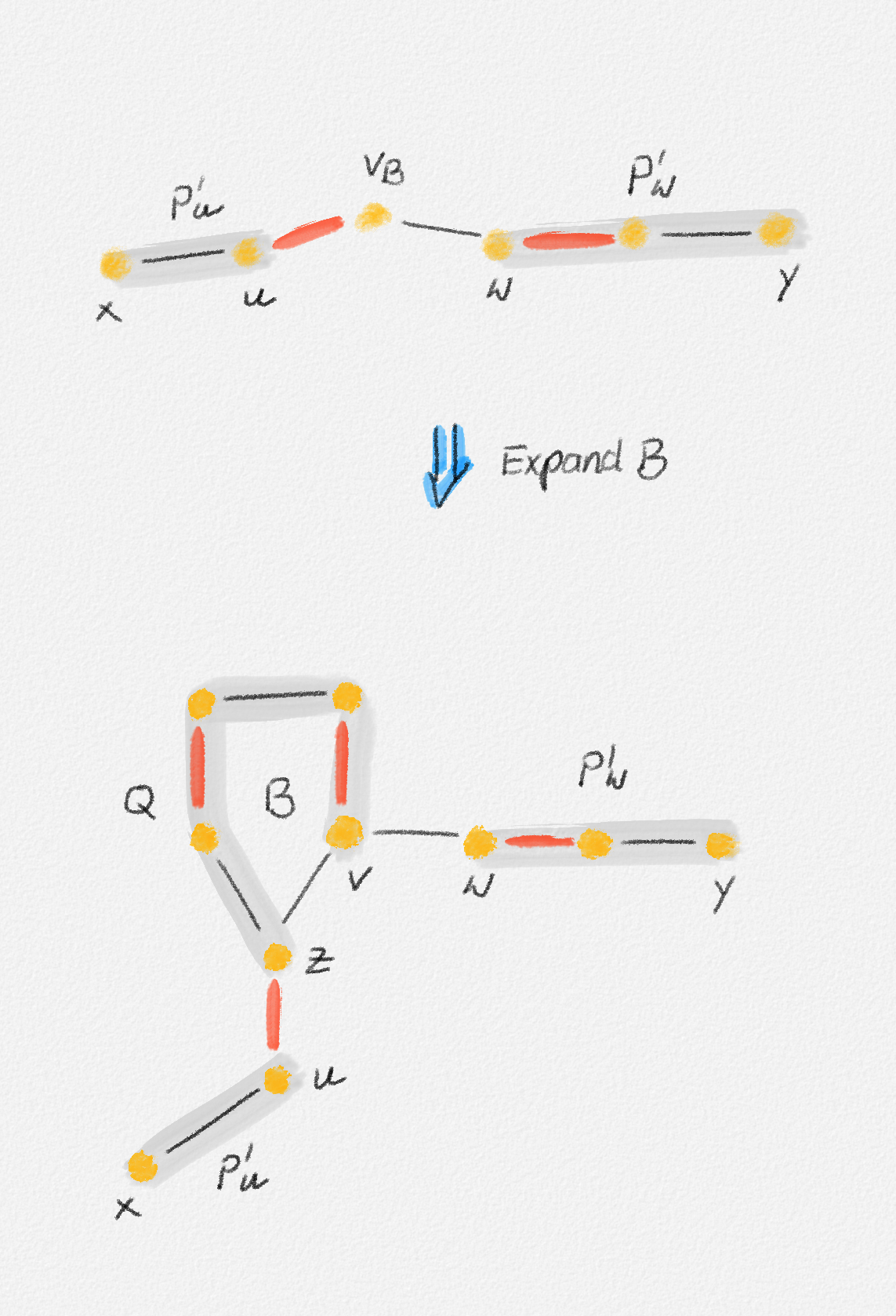
Figure 7.23: If an augmenting path \(P'\) for \(M/B\) in \(G/B\) includes \(v_B\), then it can be transformed into an augmenting path for \(M\) in \(G\) that is composed of the two subpaths of \(P'\) obtained by removing \(P'\) and an even alternating path from the base of \(B\) to another vertex in \(B\).

Since \(v \in B\), there exists an even path \(Q\) in \(B\) from \(z\) to \(v\). This path starts with an unmatched edge incident to \(z\) and ends with a matched edge incident to \(v\). By concatenating this path with \(P'_w\), we obtain an odd path \(P''_w\) from \(z\) to \(y\) in \(G\).

If \(z\) is unmatched, then \(P''_w\) is an augmenting path in \(G\). If \(z\) is matched by an edge \((u,z)\), then \((u,v_B)\) is a matched edge in \(G/B\). Thus, \(v_B \ne x\) and \((u,v_B) \in P'\). The subpath \(P'_u\) of \(P'\) from \(x\) to \(u\) is an alternating path in \(G\) whose last edge is unmatched. By concatenating \(P'_u\) and \(P''_w\), we obtain an alternating path from \(x\) to \(y\) in \(G\). Since both \(x\) and \(y\) are unmatched by \(M\), this is an augmenting path.

The construction described in this proof takes \(O(m)\) time. I leave it as an exercise for you to verify this. ▨

Lemma 7.34: Let \(B\) be a blossom in \(G\). Then \(M\) is a maximum-cardinality matching of \(G\) if and only if \(M/B\) is a maximum-cardinality matching of \(G/B\).

Proof: Lemma 7.33 shows that there exists an augmenting path for \(M\) if there exists an augmenting path for \(M/B\). Thus, \(M\) is not a maximum-cardinality matching of \(G\) if \(M/B\) is not a maximum-cardinality matching of \(G/B\).

To prove the opposite direction, assume that \(M\) is not a maximum-cardinality matching of \(G\). We need to show that \(M/B\) is not a maximum-cardinality matching of \(G/B\). Let \(M' = M \oplus S\), where \(S\) is the stem of the flow that has \(B\) as its blossom. In other words, \(S = P_z\). Since \(r_z\) is unmatched by \(M\) and the last edge in \(P_z\) is matched, \(M'\) is a matching and has size \(|M'| = |M|\). See Figure 7.24. Thus, \(M'\) is not a maximum-cardinality matching in \(G\). We have \(|M'/B| = |M'| - |M' \cap B| = |M| - |M \cap B| = |M/B|\). Thus, to prove that \(M/B\) is not a maximum-cardinality matching of \(G/B\), it suffices to prove that \(M'/B\) is not a maximum-cardinality matching of \(G/B\).

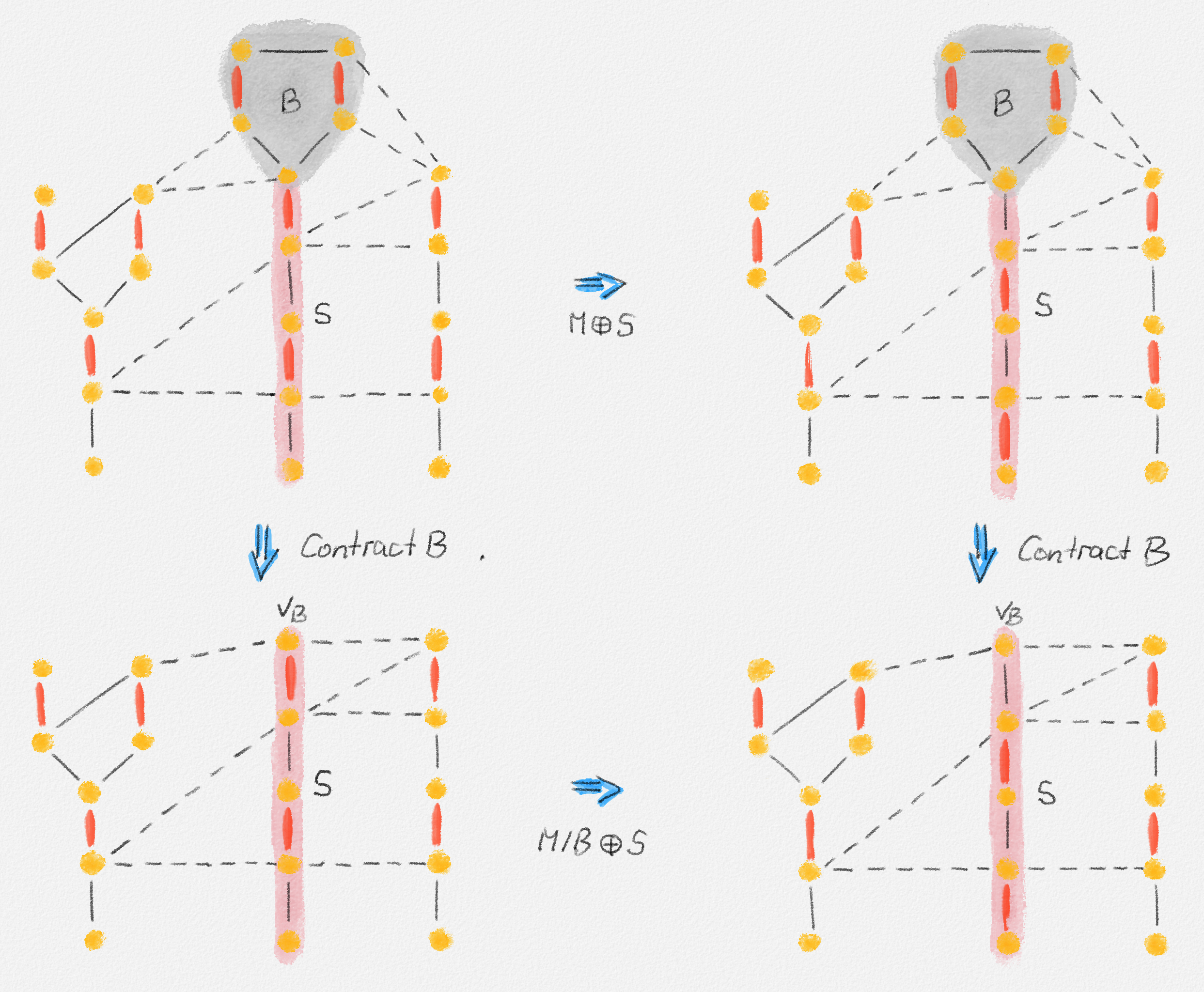
Figure 7.24: The matching in the top-right figure is the matching \(M' = M \oplus S\) obtained from the the matching \(M\) in the top-left figure. The matching \(M'/B\) in the bottom-right figure can also be obtained as \(M'/B = (M/B) \oplus S\).

The advantage of reasoning about the matchings \(M'\) and \(M'/B\) instead of the matchings \(M\) and \(M/B\) is that \(B\) is a blossom also with respect to \(M'\) but its stem is empty because \(z\) is unmatched by \(M'\). Thus, any augmenting path for \(M'\) does not interact with the flower's stem. This simplifies the construction of an augmenting path for \(M'/B\) from an augmenting path for \(M'\) considerably. In the remainder of this proof, we consider vertices and edges in \(G\) matched if they are matched by \(M'\); vertices and edges in \(G/B\) are matched if they are matched by \(M'/B\).

Consider an augmenting path \(P\) for \(M'\) in \(G\). If it does not include any vertex in \(B\), then it is a path in \(G/B\), each of its edges is matched by \(M'/B\) if and only if it is matched by \(M'\), and both endpoints are unmatched by \(M'/B\). Thus, it is an augmenting path for \(M'/B\) and \(M'/B\) is not a maximum-cardinality matching of \(G/B\). This is similar to the situation in Figure 7.22 in the proof of Lemma 7.33.

If \(P\) does include a vertex in \(B\), then observe that \(B\) includes only one unmatched vertex, \(z\), so at least one of the endpoints of \(P\) is not in \(B\). See Figure 7.25. Let \(x\) be this endpoint, let \(v\) be the vertex in \(P\) closest to \(x\) that belongs to \(B\), and let \(P'\) be the subpath of \(P\) from \(x\) to \(v\). If \(v = z\), then \(v\) is unmatched. If \(v \ne z\), then \(v\) is matched by an edge in \(M' \cap B\). In either case, the edge in \(P'\) incident to \(v\) is unmatched. The path \(P''\) obtained from \(P'\) by replacing \(v\) with \(v_B\) is an alternating path in \(G/B\). Since \(z\) is unmatched, so is \(v_B\). Since \(x\) is unmatched by \(M'\) and \(x \notin B\), it is also unmatched by \(M'/B\). Thus, \(P''\) is an augmenting path for \(M'/B\). ▨

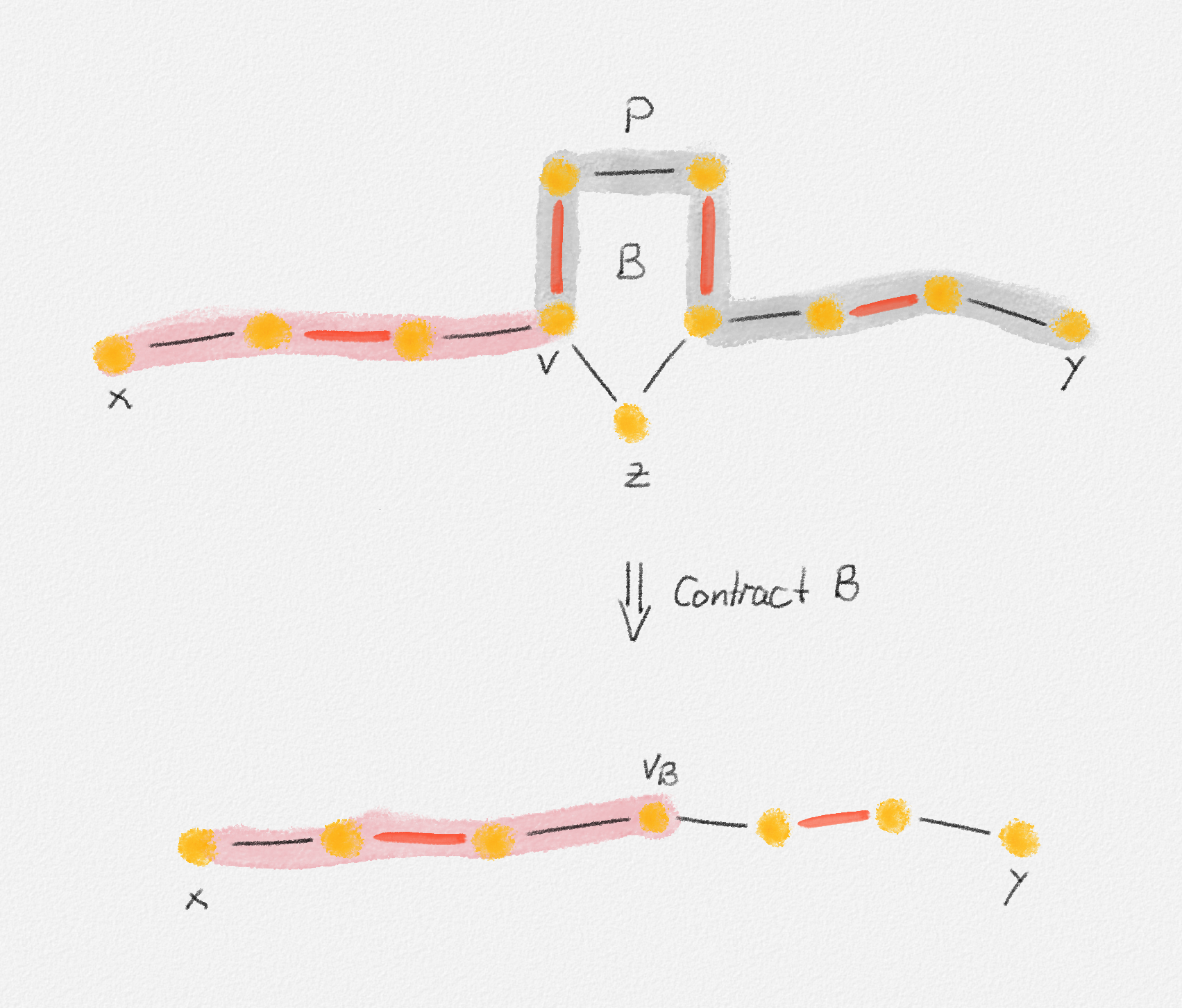
Figure 7.25: If \(P\) is an augmenting path for the matching \(M'\), then the pink subpath of \(P\) turns into an augmenting path for \(M'/B\) because \(z\) being unmatched by \(M'\) implies that \(v_B\) is unmatched by \(M'/B\).