7.4.2. Alternating Forests and Alternating BFS

A key tool in many matching algorithms is the alternating forest:

Given a graph \(G\) and a matching \(M\) in \(G\), an alternating forest is a rooted forest \(F \subseteq G\) whose roots are unmatched and such that every path in \(F\) from a root to one of its descendants is an alternating path. See Figure 7.11. Note that there is no requirement that \(F\) contains all vertices of \(G\).

For a vertex \(x \in F\), we denote the tree in \(F\) that contains \(x\) as \(T_x\), the root of \(T_x\) as \(r_x\), and the path from \(r_x\) to \(x\) in \(T_x\) as \(P_x\).

For every vertex \(x \in F\), we refer to the depth of \(x\) in \(F\), that is, to the length of \(P_x\) as \(x\)'s level \(\ell^F_x\). We call a vertex \(x \in F\) even or odd depending on whether its level is even or odd.

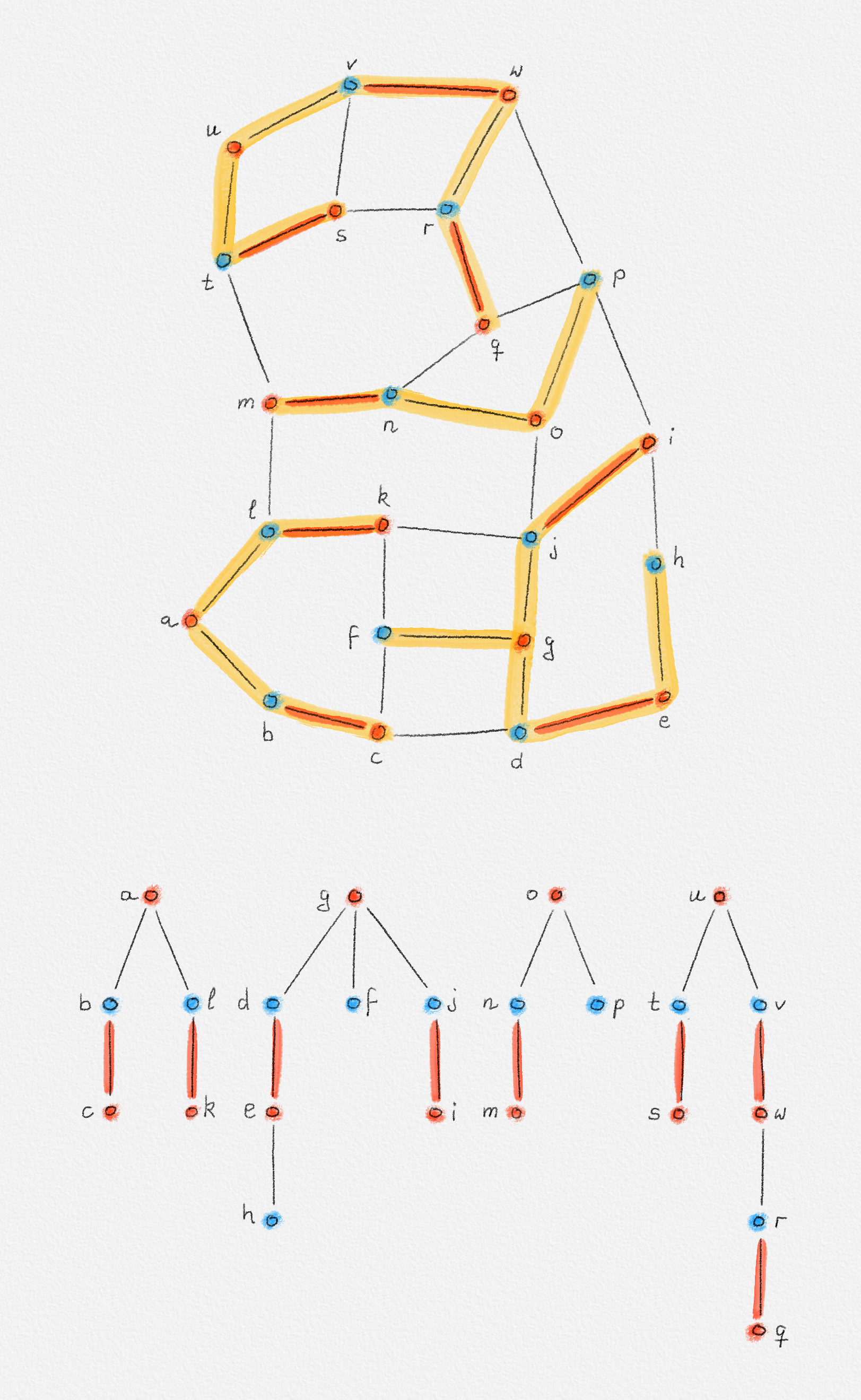
Figure 7.11: A bipartite graph \(G = (U, W, E)\). Vertices in \(U\) are red. Vertices in \(W\) are blue. The red edges form a matching of \(G\). The yellow shaded subgraph is an alternating forest of \(G\) with all unmatched vertices in \(U\) as the roots. For clarity, this forest is drawn separately below. This separate drawing highlights the level of every vertex and the fact that all top-down paths in the forest are alternating paths. Note that all vertices in \(U\) are on even levels and all vertices in \(W\) are on odd levels.

Given a bipartite graph \(G = (U, W, E)\) and set of unmatched vertices \(R \subseteq U\), we call an alternating forest \(F\) maximum for \(R\) if \(R\) is the set of roots of \(F\) and a vertex \(x\) belongs to \(F\) if and only if there exists an alternating path form a vertex in \(R\) to \(x\).

The algorithm to compute a maximum alternating forest with a given set of roots \(R\) is called alternating BFS because it operates much like breadth-first search (BFS) but alternatingly follows matched and unmatched edges:

We start by marking every vertex in \(G\) as unexplored. Then we mark the vertices in \(R\) as explored, make them the roots of \(F\), and insert them into a queue \(Q\) of vertices whose out-edges are to be explored. Note that this ensures that all vertices in \(Q\) are even and in \(U\). We maintain this invariant throughout the algorithm.

Now, as long as \(Q\) is not empty, we remove the next vertex \(u\) from the head of \(Q\) and inspect all its out-edges. For every edge \((u,w)\) such that \(w\) is unexplored, we mark \(w\) as explored and make \(w\) a child of \(u\) in \(F\). If \(w\) is matched by an edge \((u',w)\), then we also mark \(w\)'s mate \(u'\) as explored, make it \(w\)'s child in \(F\), and add \(u'\) to the end \(Q\). This ensures that \(u'\) is even. Since \(u \in U\) and \(G\) is bipartite, we have \(w \in W\) and \(u' \in U\). So the invariant that \(Q\) contains only even vertices in \(U\) is maintained. Note that we do not need to check whether \(u'\) is explored: Since \(w\) was unexplored and we always add the two endpoints of a matched edge to \(F\) together, \(u'\) is explored if and only if \(w\) is explored.

The final forest \(F\) is the one we obtain once \(Q = \emptyset\).

By the next exercise and lemma, this forest \(F\) is indeed a maximum alternating forest with the vertices in \(R\) as its roots, and this procedure to compute \(F\) takes \(O(n + m)\) time.

Exercise 7.5: Prove that alternating BFS takes \(O(n + m)\) time.

Lemma 7.10: Given a bipartite graph \(G = (U, V, E)\) and a set \(R \subseteq U\) of unmatched vertices, alternating BFS computes a maximum alternating forest \(F\) with the vertices in \(R\) as its roots.

Proof: The forest \(F\) computed by alternating BFS is clearly alternating: Every vertex \(u \in Q\) is even and explored. Thus, if it has a mate, this mate is also explored. Therefore, the child edges of \(u\) added to \(F\) are unmatched. We add a child \(u' \in U\) to an odd vertex \(w\) only if \(u'\) is \(w\)'s mate. Thus, the child edges of odd vertices are matched. Since the child edges of all even vertices are unmatched and the child edges of all odd vertices are matched, \(F\) is an alternating forest.

It remains to prove that \(F\) is maximum for \(R\), that is, that a vertex \(x\) belongs to \(F\) if and only if it can be reached from a vertex in \(R\) via an alternating path.

The "only if" direction is easy because, for every vertex \(x \in F\), the path \(P_x\) is an alternating path from \(r_x \in R\) to \(x\).

For the "if" direction, consider all vertices \(x\) with an alternating path from a vertex in \(R\) to \(x\). For each such vertex \(x\), let \(A_x\) be a shortest alternating path with \(x\) as one of its endpoints and with its other endpoint, \(u_x\), in \(R\). We use induction on \(|A_x|\) to prove that \(x \in F\).

If \(|A_x| = 0\), then \(x = u_x\) and \(x \in R\). Since every vertex in \(R\) is the root of a tree in \(F\), this implies that \(x \in F\).

If \(|A_x| > 0\), then let \(y\) be \(x\)'s predecessor in \(A_x\). The subpath of \(A_x\) from \(u_x\) to \(y\) is an alternating path from \(u_x\) to \(y\) of length less than \(|A_x|\). Since \(A_y\) is a shortest alternating path with \(y\) as one of its endpoints and with the other endpoint in \(R\), this implies that \(|A_y| < |A_x|\). Thus, by the induction hypothesis, \(y \in F\).

If \(x \in U\), then \(A_x\) has even length because \(G\) is bipartite and both endpoints of \(A_x\) are in \(U\). Since \(u_x\) is unmatched, this implies that the edge \((y,x)\) is matched. Since mates are added to \(F\) together and \(y \in F\), this implies that \(x \in F\).

If \(x \in W\), then \(A_x\) has odd length because \(G\) is bipartite and \(A_x\) has one endpoint in \(U\) and the other in \(W\). Since \(u_x\) is unmatched, this implies that the first and last edges of \(A_x\) are both unmatched. Specifically, the edge \((y,x)\) is unmatched. Since \(x \in W\), we have \(y \in U\) because \(G\) is bipartite. Thus, the path \(P_y\) from \(r_y\) to \(y\) in \(F\) has even length. Therefore, \(y\) is even and alternating BFS explores all unmatched edges incident to \(y\). When exploring the edge \((y,x)\), \(x\) becomes \(y\)'s child in \(F\) unless \(x\) is already in \(F\). In either case, \(x \in F\). ▨

Lemma 7.11: Given a bipartite graph \(G\) and a matching \(M\) of \(G\), it takes \(O(n + m)\) time to decide whether there exists an augmenting path \(P\) for \(M\) and, if so, find such a path.

Proof: We use alternating BFS to construct a maximum alternating forest \(F\) whose roots are all the unmatched vertices in \(U\). If \(F\) contains an unmatched vertex \(w \in W\), then the path \(P_w\) from \(r_w\) to \(w\) in \(F\) is an augmenting path because it is an alternating path and both its endpoints are unmatched. Conversely, if there exists an augmenting path \(P\) for \(M\), then it has odd length and therefore must have one endpoint, \(u\), in \(U\) and the other, \(w\), \(W\). Since \(u\) is unmatched, this shows that there exists an alternating path from an unmatched vertex in \(U\) to \(w\). Since \(F\) is a maximum alternating forest, \(w\) is therefore in \(F\).

The algorithm takes \(O(n + m)\) time to construct \(F\), by Exercise 7.5. Given \(F\), it takes \(O(n)\) time to inspect all vertices in \(F\) to check whether one of them is in \(W\) and is unmatched. If we find such a vertex \(w\), we follow parent pointers in \(F\) to construct the augmenting path \(P_w\). Thus, the entire algorithm takes \(O(n + m)\) time. ▨