7.3.1. Maximum-Cardinality Matching

Let us start with finding a maximum-cardinality matching in a bipartite graph \(G = (U, W, E)\). To find such a matching, we augment \(G\) with two new vertices \(s\) and \(t\). Every vertex in \(U\) becomes an out-neighbour of \(s\), every vertex in \(W\) becomes an in-neighbour of \(t\), and every edge of \(G\) gets directed from its endpoint in \(U\) to its endpoint in \(W\). Finally, we give every edge a capacity of \(1\). Let us call the resulting graph \(\vec{G}\). This construction is illustrated in Figure 7.6.

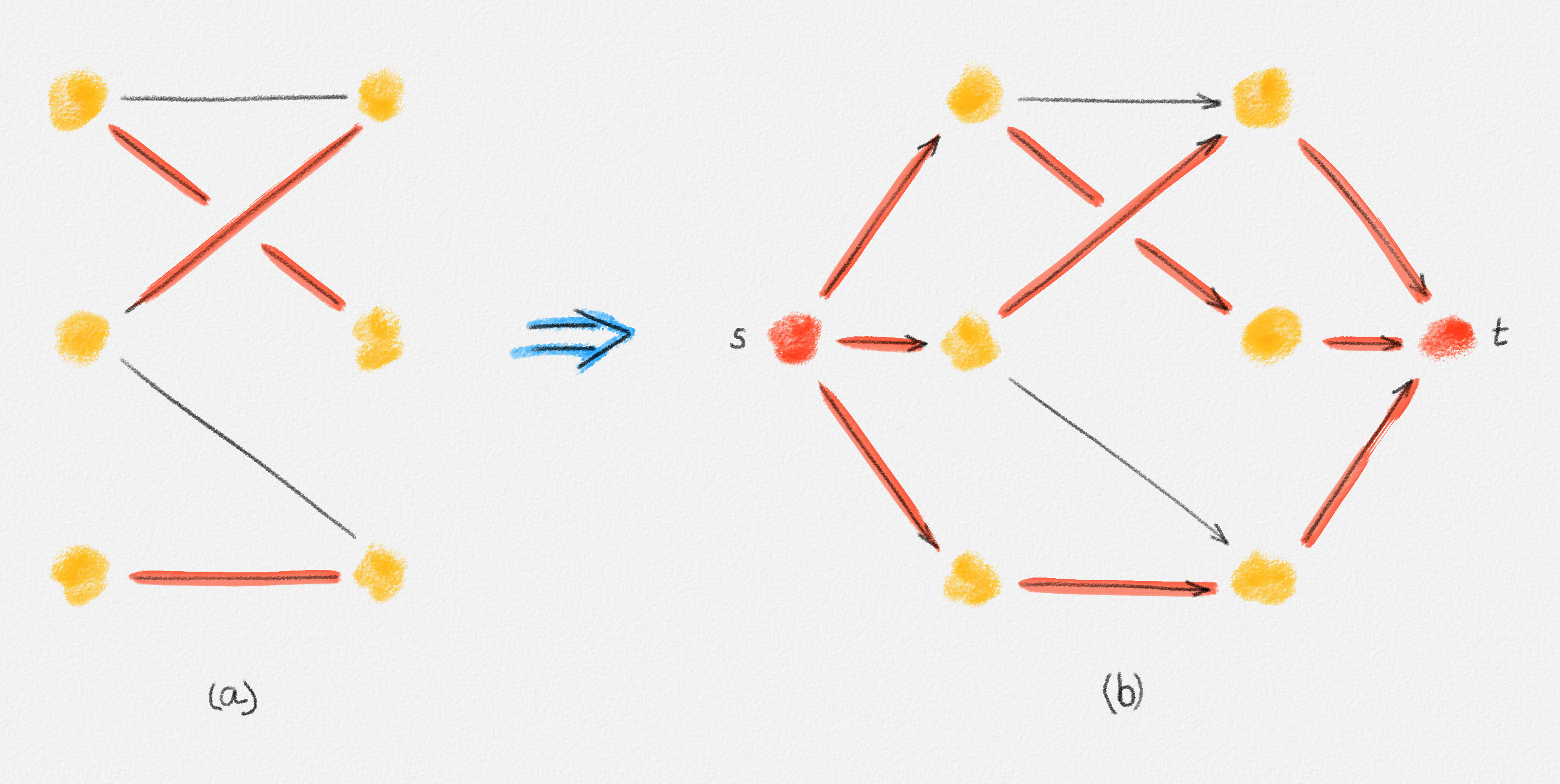
Figure 7.6: (a) A bipartite graph \(G\) and a maximum-cardinality matching shown in red. (b) The graph \(\vec{G}\) constructed from \(G\) by directing all edges from left to right, adding two vertices \(s\) and \(t\), and making all vertices in \(U\) out-neighbours of \(s\) and all vertices in \(W\) in-neighbours of \(t\). All edges have capacity \(1\). The maximum-flow corresponding to the maximum matching in (a) sends one unit of flow along each of the red \(st\)-paths.

Lemma 7.3: \(M\) is a matching in \(G\) if and only if there exists an integral \(st\)-flow \(f\) in \(\vec{G}\) such that \(M = \{e \in G \mid f_e = 1\}\).

Proof: First assume that \(M\) is a matching. Then set \(f_{s,u} = f_{u,w} = f_{w,t} = 1\) for every edge \((u,w) \in M\) and \(f_e = 0\) for any other edge. Clearly, \(f\) is integral and satisfies the capacity constraints of all edges in \(\vec{G}\). For every vertex \(u \in G\), if \(u\) is unmatched, then \(f_{s,u} = 0\) and \(f_{u,w} = 0\) for every edge \((u,w) \in G\). If \(u\) is matched, then \(f_{s,u} = 1\) and \(f_{u,w} = 1\) for exactly one edge \((u,w) \in G\) because \(M\) is a matching. Thus, \(f\) satisfies \(u\)'s flow conservation constraint whether \(u\) is matched or not. A similar argument shows that \(f\) satisfies the flow conservation constraints of all vertices in \(W\). Thus, \(f\) is an \(st\)-flow.

Now assume that \(f\) is an integral \(st\)-flow in \(\vec{G}\). By the flow conservation constraint, we have \(\sum_{w \in W} f_{u,w} = f_{s,u} \le 1\) for every vertex \(u \in U\). Since \(f\) is integral, this shows that there exists at most one edge \((u,w) \in G\) such that \(f_{u,w} = 1\). By an analogous argument, there exists at most one edge \((u,w) \in G\) such that \(f_{u,w} = 1\) for every vertex \(w \in W\). Thus, the set \(M = \{e \in G \mid f_e = 1\}\) is a matching in \(G\). ▨

Corollary 7.4: A maximum-cardinality matching of a bipartite graph \(G\) can be found in \(O\bigl(n^2 \sqrt{m}\bigr)\) time.

Proof: Constructing \(\vec{G}\) from \(G\) takes \(O(n + m)\) time. By Theorem 5.34, we can find a maximum flow \(f\) in \(\vec{G}\) in \(O\bigl(n^2 \sqrt{m}\bigr)\) time. By Observation 5.35, this flow is integral. Thus, by Lemma 7.3, the set \(M = \{e \in G \mid f_e = 1\}\) is a matching in \(G\). Constructing \(M\) from \(f\) takes \(O(n + m)\) time. Overall, computing \(M\) thus takes \(O\bigl(n^2\sqrt{m}\bigr)\) time.

Since \(U \cup \{s\}\) is an \(st\)-cut in \(\vec{G}\) and every edge in \(G\) crosses this cut, we have \(|M| = F_s\), by Lemma 5.3. If \(M\) is not a maximum-cardinality matching, then there exists a matching \(M'\) such that \(|M'| > |M|\). By Lemma 7.3, \(M' = \{e \in G \mid f'_e = 1\}\), for some integral \(st\)-flow \(f'\) in \(\vec{G}\). Again, since \(U \cup \{s\}\) is an \(st\)-cut, we have \(F'_s = |M'| > |M| = F_s\), a contradiction because \(f\) is a maximum flow in \(\vec{G}\). This proves that \(M\) is a maximum-cardinality matching in \(G\). ▨