7.4.4.1. The Level Graph

This section introduces the level graph \(L^M\) for a matching \(M\) of a bipartite graph and shows how to compute \(L^M\) and how use it to find an inclusion-maximal set of shortest augmenting paths, all in \(O(n + m)\) time.

Given a bipartite graph \(G = (U, W, E)\), a subset of unmatched vertices \(R \subseteq U\), and some vertex \(x \in G\), a shortest alternating path from \(\boldsymbol{R}\) to \(\boldsymbol{x}\) is a shortest alternating path \(P\) with the property that one of its endpoints is \(x\) and the other endpoint is in \(R\).

Exercise 7.6: Let \(G = (U, W, E)\) be a bipartite graph, let \(R \subseteq U\) be a subset of unmatched vertices in \(U\), and let \(F\) be a maximum alternating forest of \(G\) with \(R\) as its set of roots computed using alternating BFS. Prove that for every vertex \(x \in F\), the path \(P_x\) from \(r_x \in R\) to \(x\) is a shortest alternating path from \(R\) to \(x\).

Exercise 7.7: Let \(G = (U, W, E)\) be a bipartite graph, let \(R \subseteq U\) be a subset of unmatched vertices in \(U\), and let \(P\) be a shortest alternating path from \(R\) to some vertex \(x\). Let \(r \in R\) be the other endpoint of \(P\), and let \(y\) be any vertex in \(P\). Prove that the subpath of \(P\) from \(r\) to \(y\) is a shortest alternating path from \(R\) to \(y\).

Given a bipartite graph \(G = (U, W, E)\) and a matching \(M\) in \(G\), let \(U' \subseteq U\) be the subset of all unmatched vertices in \(U\), and let \(k\) be the length of a shortest augmenting path for \(M\). If no such path exists, then \(M\) is a maximum matching and \(k = \infty\).

The level graph \(L^M \subseteq G\) is a subgraph of \(G\) containing exactly all vertices \(x \in G\) that can be reached from a vertex in \(U'\) via an alternating path of length at most \(k\). An edge \(e \in G\) belongs to \(L^M\) if and only if it belongs to a shortest alternating path of length at most \(k\) from \(U'\) to some vertex \(x \in L^M\). This is illustrated in Figure 7.12.

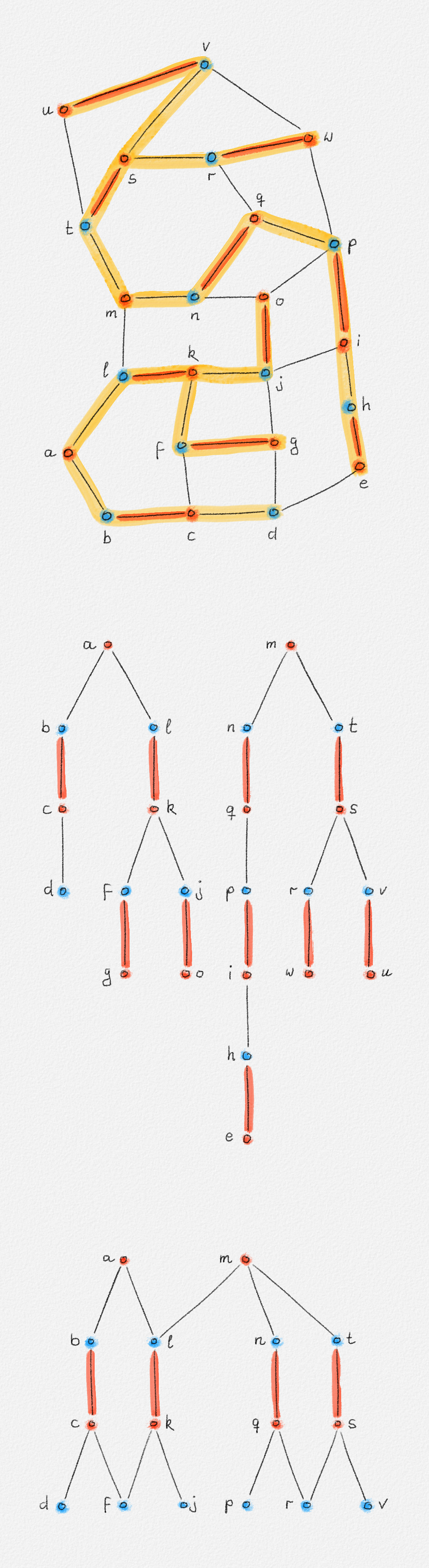
Figure 7.12: A bipartite graph \(G = (U, W, E)\). Vertices in \(U\) are red. Vertices in \(W\) are blue. The red edges form a matching \(M\) of \(G\). An alternating forest of \(G\) with respect to \(M\) is shaded and, for clarity, drawn separately below \(G\). The level graph \(L^M\) of \(G\) with respect to \(M\) is shown below the alternating forest.

Lemma 7.15: The level graph \(L^M\) for a bipartite graph \(G = (U, W, E)\) and a matching \(M\) of \(G\) can be constructed in \(O(n + m)\) time.

Proof: Let \(U' \subseteq U\) be the set of all unmatched vertices in \(U\). We start by constructing a maximum alternating forest \(F\) with \(U'\) as its set of roots, using alternating BFS. By Lemma 7.10, this takes \(O(n + m)\) time.

Since \(F\) is maximum, it contains exactly those vertices in \(G\) that are reachable from \(U'\) via alternating paths. Thus, the vertex set of \(F\) is a superset of the vertex set of \(L^M\). By Exercise 7.6, the path \(P_x\) from \(r_x\) to \(x\) in \(F\) is a shortest alternating path from \(U'\) to \(x\), for all \(x\). Thus, if \(k\) is the minimum level such that \(F\) contains an unmatched vertex \(w \in W\) at level \(k\), then the vertex set of \(L^M\) is exactly the set of vertices in \(F\) at levels \(0, \ldots, k\). If \(F\) contains no unmatched vertex in \(W\), then \(k = \infty\). To obtain the vertex set of \(L^M\), we remove all vertices at levels greater than \(k\) from \(F\). This takes \(O(n)\) time.

To construct the edge set of \(L^M\), we inspect all edges of \(G\) and include an edge \((x,y)\) in the edge set of \(L^M\) if and only if \(x\) and \(y\) belong to \(L^M\) and either

• \((x,y) \in M\), \(\ell^F_x = 2i-1\), and \(\ell^F_y = 2i\), for some \(i \in \mathbb{N}\), or
• \((x,y) \notin M\), \(\ell^F_x = 2i\), and \(\ell^F_y = 2i+1\), for some \(i \in \mathbb{N}\).

This takes \(O(m)\) time, so the total cost of this procedure is \(O(n + m)\), as claimed. We need to prove that the graph \(H\) it produces is indeed \(L^M\).

Since we already observed that the vertices at levels \(0, \ldots, k\) in \(F\) are exactly the vertices reachable from \(U'\) via augmenting paths of length at most \(k\), \(H\) and \(L^M\) have the same vertex set. It remains to prove that \(H\) includes an edge \(e\) if and only if \(L^M\) includes this edge, that is, if and only if there exists a shortest alternating path from \(U'\) to some vertex \(x \in L^M\) that includes \(e\).

"Only if": Consider an edge \((x, y)\) that we add to \(H\). Then \(\ell^F_y = \ell^F_x + 1\).

If \(x\) is even, then \(P_x\) ends in a match edge and \((x, y) \notin M\). Since \(\ell_z^F \le \ell_x^F < \ell_y^F\) for every vertex \(z \in P_x\), we have \(y \notin P_x\), so adding \((x,y)\) to \(P_x\) gives an alternating path of length \(\ell_x^F + 1 = \ell_y^F\) from \(r_x\) to \(y\).

If \(x\) is odd, then \(P_x\) ends in an unmatched edge and \((x, y) \in M\). Moreover, every vertex \(z \in P_x\) satisfies \(\ell_z^F \le \ell_x^F < \ell_y^F\), so \(z \ne y\). Thus, once again, adding \((x,y)\) to \(P_x\) gives an alternating path of length \(\ell_x^F + 1 = \ell_y^F\) from \(r_x\) to \(y\).

In both cases, we obtain an alternating path of length \(\ell_y^F\) from \(U'\) to \(y\). Since this path has length \(\ell_y^F\), it is a shortest alternating path from \(U'\) to \(y\). Thus, there exists a shortest alternating path from \(U'\) to \(y\) that includes the edge \((x,y)\).

"If": Consider an edge \((x,y)\) in a shortest alternating path \(A\) from \(U'\) to some vertex \(z \in L^M\). Let \(u\) be the endpoint of \(A\) in \(U'\). Then \(x, y \in L^M\), and we already observed that this implies that \(x, y \in F\), so their levels \(\ell^F_x\) and \(\ell^F_y\) are well defined. By Exercise 7.7, the subpaths \(A_x\) and \(A_y\) of \(A\) from \(u\) to \(x\) and \(y\), respectively, are shortest alternating paths from \(U'\) to \(x\) and \(y\), respectively. Thus, by Exercise 7.6, \(\ell^F_x = |A_x|\), \(\ell^F_y = |A_y|\), and therefore, \(\ell^F_y = \ell^F_x + 1\).

If \(x \in U\), then \(A_x\) and \(P_x\) are even because \(G\) is bipartite. Thus, \((x, y) \notin M\). By the above rules, we add \((x, y)\) to \(H\) in this case.

If \(x \in W\), then \(A_x\) and \(P_x\) are odd. Thus, \((x, y) \in M\) and, once again, we add \((x,y)\) to \(H\) by the above rules.

This shows that we add exactly the edges of \(L^M\) to \(H\), that is, \(H\) and \(L^M\) have the same vertex and edge sets and are thus the same graph. ▨

Lemma 7.16: An inclusion-maximal set of shortest augmenting paths can be found in \(O(n + m)\) time.

Proof: Once again, let \(U' \subseteq U\) be the subset of unmatched vertices in \(U\), and let \(k\) be the length of a shortest augmenting path for \(M\). We start by constructing the level graph \(L^M\) of \(M\), using Lemma 7.15. We turn \(L^M\) into a directed graph by directing the edges in \(L^M\) from vertices at lower levels to vertices at higher levels.

If \(L^M\) contains no unmatched vertex in \(W\), then \(M\) is a maximum-cardinality matching, and we return the empty set (there are no augmenting paths). So assume that there exists an augmenting path and, therefore, that \(k < \infty\).

We iterate over the vertices in \(U'\). For each such vertex \(u\), we run DFS in \(L^M\) from \(u\). The search ends as soon as we have explored all vertices reachable from \(u\) or we find an unmatched vertex in \(W\), whichever comes first. If we find an unmatched vertex \(w \in W\), then the path \(P\) from \(u\) to \(w\) explored by the search is an augmenting path of length \(k\) because all unmatched vertices in \(W\) that are in \(L^M\) are at level \(k\) in \(L^M\) and all edges in \(L^M\) connect vertices on consecutive levels and are directed from vertices on lower level to vertices on higher levels. Thus, we add this path \(P\) to \(A\). No vertex in \(P\) can be part of another augmenting path in any inclusion-maximal set of shortest augmenting paths that includes \(P\). Any vertex not in \(P\) that is explored by the search for \(P\) cannot reach any unexplored vertex at level \(k\) in \(L^M\) and thus is not part of any augmenting path of length \(k\) either. Thus, all vertices explored by the current search can be ignored by subsequent searches for shortest augmenting paths starting from other vertices in \(U'\). By removing all vertices explored by the current search and their incident edges before advancing to the next vertex in \(U'\), we ensure that every vertex and every edge in \(L^M\) is explored by at most one search from a vertex in \(U'\) and the total cost of all searches is \(O(n + m)\). (This argument is analogous to finding a blocking flow in \(O(nm)\) time in Dinitz's maximum flow algorithm.)

To see that the set \(A\) of paths obtained after the final search in \(L^M\) is an inclusion-maximal set of shortest augmenting paths, observe first that it is a set of vertex-disjoint shortest augmenting paths because every path in \(L^M\) is alternating; we add a path to \(A\) only if both its endpoints are unmatched and, thus, its length is \(k\); and we explicitly ensure that all paths in \(A\) are vertex-disjoint.

To see that no superset of \(A\) is a vertex-disjoint set of shortest augmenting paths, consider an arbitrary augmenting path \(P\) of length \(k\). One of the endpoints of \(P\) is a vertex \(u \in U'\). If \(P\) is vertex-disjoint from every path in \(A\), then none of the vertices in \(P\) is removed from \(L\) before the search from \(u\) starts. Indeed, we argued above that any previous search removes only vertices in augmenting paths found so far and vertices that do not belong to any shortest augmenting path. Thus, when we start the DFS from \(u\), there exists a path of length \(k\) in \(L\) from \(u\) to an unmatched vertex \(w\). The search finds such a path and adds it to \(A\), a contradiction because we assumed that \(P\) is vertex-disjoint from every path in \(A\). ▨