7.7.1.1. Finding and Contracting Blossoms
To find an augmenting path for the current matching \(M\), Edmonds's algorithm starts by computing an alternating forest \(F\) of \(G\) with all unmatched vertices in \(G\) as roots.
Recall that we call a vertex odd or even depending on whether its depth in \(F\) is odd or even. The first lemma in this section states a sufficient, but not necessary, condition under which \(M\) is a maximum-cardinality matching:
Lemma 7.31: If there is no unmatched edge \((x,y) \notin F\) such that \(x\) and \(y\) are both even vertices in \(F\), then \(M\) is a maximum-cardinality matching.
Proof: We prove the contrapositive: If \(M\) is not a maximum-cardinality matching, then there must exist an unmatched edge \((x,y)\) such that \(x\) and \(y\) are both even vertices in \(F\).
If \(M\) is not a maximum-cardinality matching, then there exists an augmenting path \(P\) for \(M\). We partition \(P\) into maximal subpaths \(P_0, \ldots, P_{k+1}\) such that each such subpath contains only edges in \(F\). See Figure 7.18.
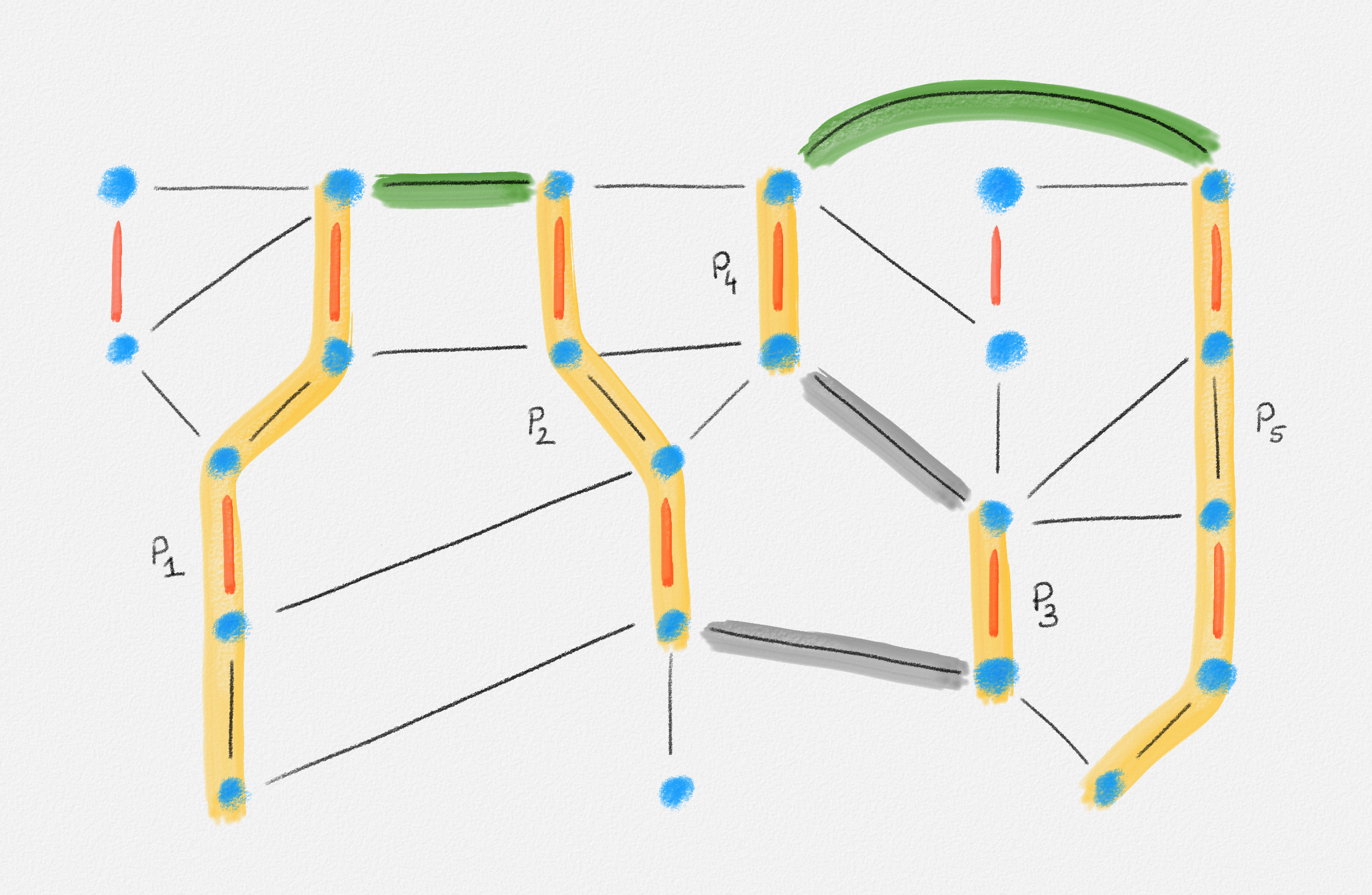
Figure 7.18: The path shaded in yellow, grey, and green is an augmenting path \(P\). The yellow paths are the subpaths \(P_1, P_2, P_3, P_4, P_5\) of \(P\) that stay within a single tree in \(F\). Note that each of the paths \(P_2, P_3, P_4\) has an odd and an even endpoint. The grey and green edges are the edges in \(P\) that connect the paths \(P_1, P_2, P_3, P_4, P_5\). Of these, the two green edges are edges with two even endpoints.
For \(0 \le i \le k+1\), let \(x_i\) be the first vertex of \(P_i\), and let \(y_i\) be the last vertex of \(P_i\). We prove that \(y_0\) is an even vertex, \(x_{k+1}\) is an even vertex and, for \(1 \le i \le k\), either \(x_i\) or \(y_i\) is an even vertex. Since \(y_0\) is an even vertex, there exists a maximum index \(0 \le i \le k\) such that \(y_i\) is even. If \(i = k\), then \(x_{i+1} = x_{k+1}\) is even. If \(i < k\), then \(y_{i+1}\) is odd, so \(x_{i+1}\) is even. Since \(y_i\) is even and \(x_{i+1}\) is even, the edge \((y_i, x_{i+1})\) is an edge not in \(F\) connecting two even vertices. Since even vertices in \(F\) are matched by edges in \(F\), this edge is unmatched. The lemma follows.
First consider the path \(P_0\). If \(P_0 = \langle x_0 \rangle\), then \(y_0 = x_0\). Since \(x_0\) is unmatched, \(y_0\) is even in this case. If \(P_0 \ne \langle x_0 \rangle\), then \(y_0\) is a matched vertex because \(y_0 \in T_{x_0}\) and \(x_0\) is the only unmatched vertex in \(T_{x_0}\). Since \(y_{k+1}\) is unmatched, this implies that \(y_0 \ne y_{k+1}\), so \(k \ge 0\) and \(y_0\) has a successor \(x_1\) in \(P\). Next observe that \(P_0 = P_{y_0}\) because \(x_0\) is the root of \(T_{x_0}\), \(y_0 \in T_{x_0}\), and all edges in \(P_0\) belong to \(T_{x_0}\). Thus, if \(y_0\) were odd, then the last edge in \(P_0\) would be unmatched. Since \(P\) is an alternating path, this would imply that the edge \((y_0,x_1)\) would have to be matched and \(x_1\) would be in \(T_{x_0}\), a contradiction. This shows that \(y_0\) is even. An analogous argument shows that \(x_{k+1}\) is even.
Now consider any path \(P_i\) with \(1 \le i \le k\). Since \(x_i\) is reachable from \(x_0\) via an alternating subpath of \(P\), we have \(x_i \in F\). Since \(x_0\) and \(y_{k+1}\) are the only unmatched vertices in \(P\), all vertices in \(P_i\) are matched. In particular, \(x_i\) and \(y_i\) are matched. If the edge in \(P_i\) incident to \(x_i\) were unmatched, then the edge \((y_{i-1}, x_i)\) in \(P\) would have to be matched because \(P\) is an alternating path. Thus, \(y_{i-1}\) would be in \(T_{x_i}\), a contradiction. This shows that the edge in \(P_i\) incident to \(x_i\) is matched. By an analogous argument, the edge in \(P_i\) incident to \(y_i\) is matched. Thus, the first and last edges of \(P_i\) are matched and \(P_i\) has odd length. Since \(P_i\) is an alternating path in \(T_{x_i}\), either \(x_i\) is an ancestor of \(y_i\) in \(T_{x_i}\) or vice versa. Thus, since \(P_i\) has odd length, exactly one of \(x_i\) and \(y_i\) is even. ▨
Based on Lemma 7.31, the search for an augmenting path in Edmonds's algorithm employs the following strategy: We inspect all edges of \(G\).
-
If we find no unmatched edge \((x, y) \notin F\) such that both \(x\) and \(y\) are even, then by Lemma 7.31, \(M\) is a maximum-cardinality matching. Thus, we report that there is no augmenting path.
-
If we do find an unmatched edge \((x, y) \notin F\) such that both \(x\) and \(y\) are even, then there are two possibilities:
-
\(x\) and \(y\) belong to different trees in \(F\). As illustrated in Figure 7.19, the union of \(P_x\), \(P_y\), and the edge \((x, y)\) is an augmenting path \(P\) from \(r_x\) to \(r_y\) in this case. The search for an augmenting path terminates and we return \(P\).
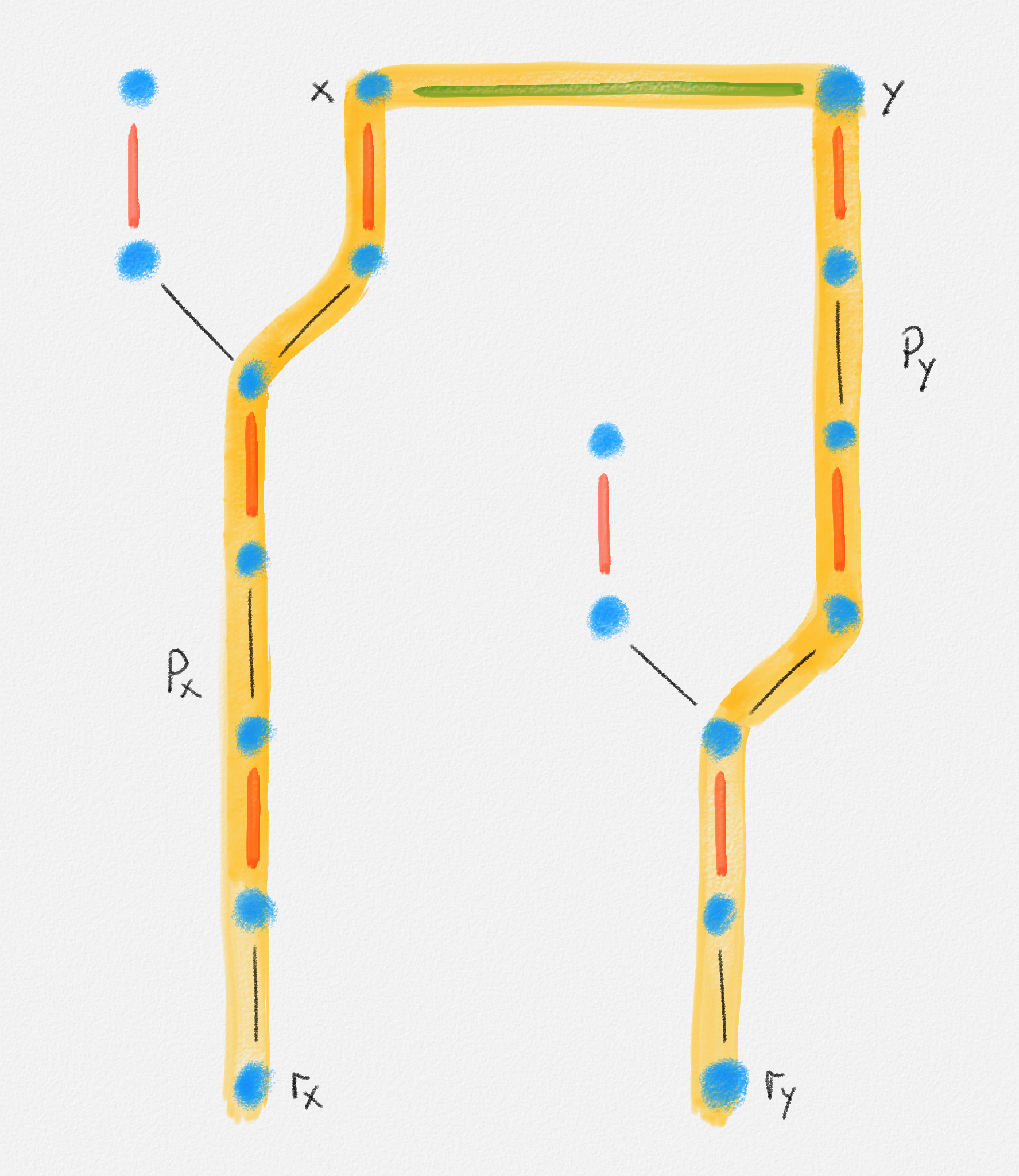
Figure 7.19: The green edge is an edge \((x, y)\) connecting two vertices in different trees of \(F\). This edge together with the two paths \(P_x\) and \(P_y\) forms the yellow path, which is an augmenting path from \(r_x\) to \(r_y\).
-
\(x\) and \(y\) belong to the same tree in \(F\). In this case, \(P_x\) and \(P_y\) have at least one vertex in common, namely \(r_x\). We partition the edge set \(P_x \cup P_y \cup \{(x,y)\}\) into two subsets. The first subset, \(B\), contains \((x,y)\) and all edges in \(P_x \oplus P_y\). The second subset, \(S\), contains all edges in \(P_x \cap P_y\). This is illustrated in Figure 7.20.
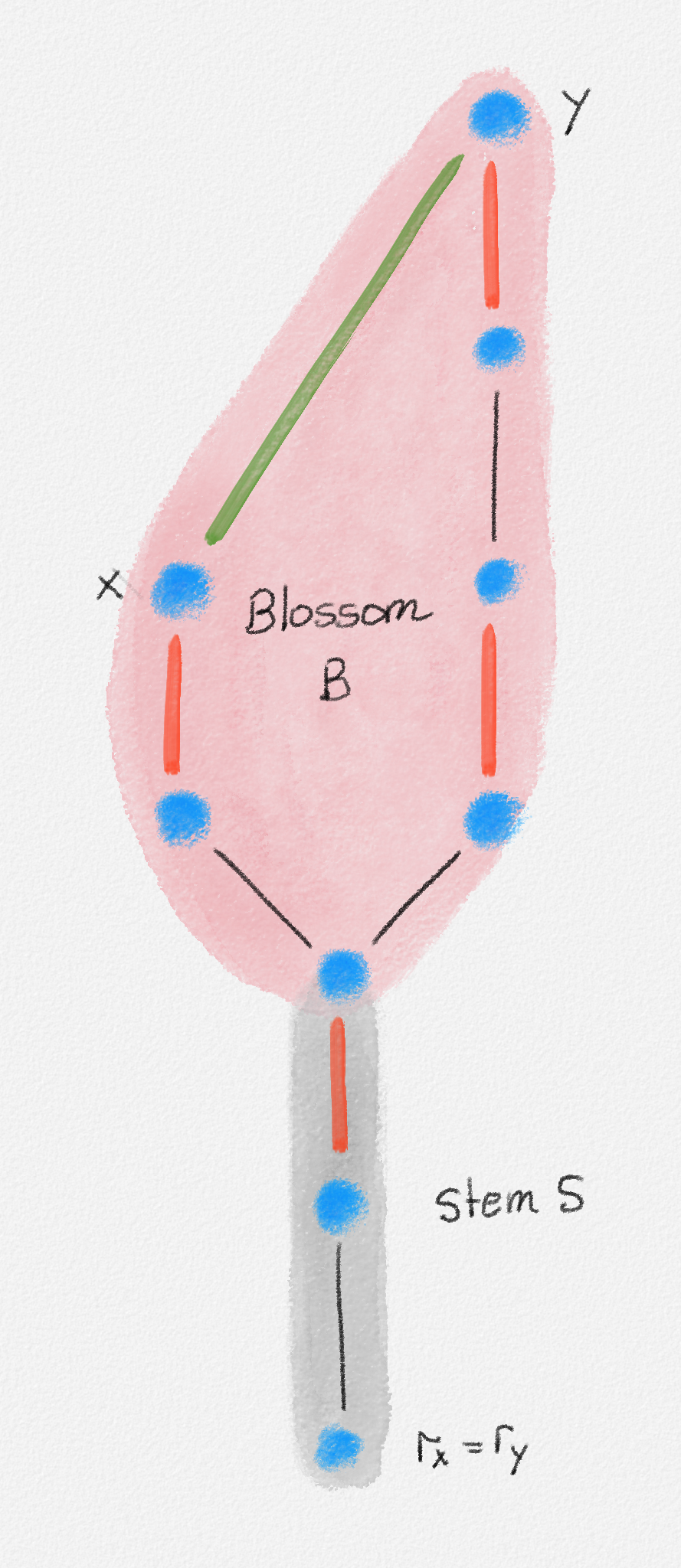
Figure 7.20: A blossom formed by an edge \((x,y)\) connecting two even vertices in the same tree of \(F\). The blossom is shaded pink. The stem \(S\) of the blossom is shaded grey.
In this case, we call \(B \cup S\) a flower. \(B\) is its blossom. \(S\) is its stem. One endpoint of \(S\) is \(r_x\). The other endpoint, \(z\), is the only vertex shared by \(B\) and \(S\). We call \(z\) the base of the blossom \(B\). Note that the stem \(S\) may be empty (contain no edges), in which case \(z = r_x\).
Let \(G/B\) be the graph obtained from \(G\) by contracting the blossom \(B\). What this means is that we remove all vertices in \(B\) and introduce a new vertex \(v_B\) representing the whole blossom. For every edge \((v, w) \in G\) with exactly one endpoint in \(B\), say \(w\), we introduce the edge \((v, v_B)\) into \(G/B\). This construction is illustrated in Figure 7.21.
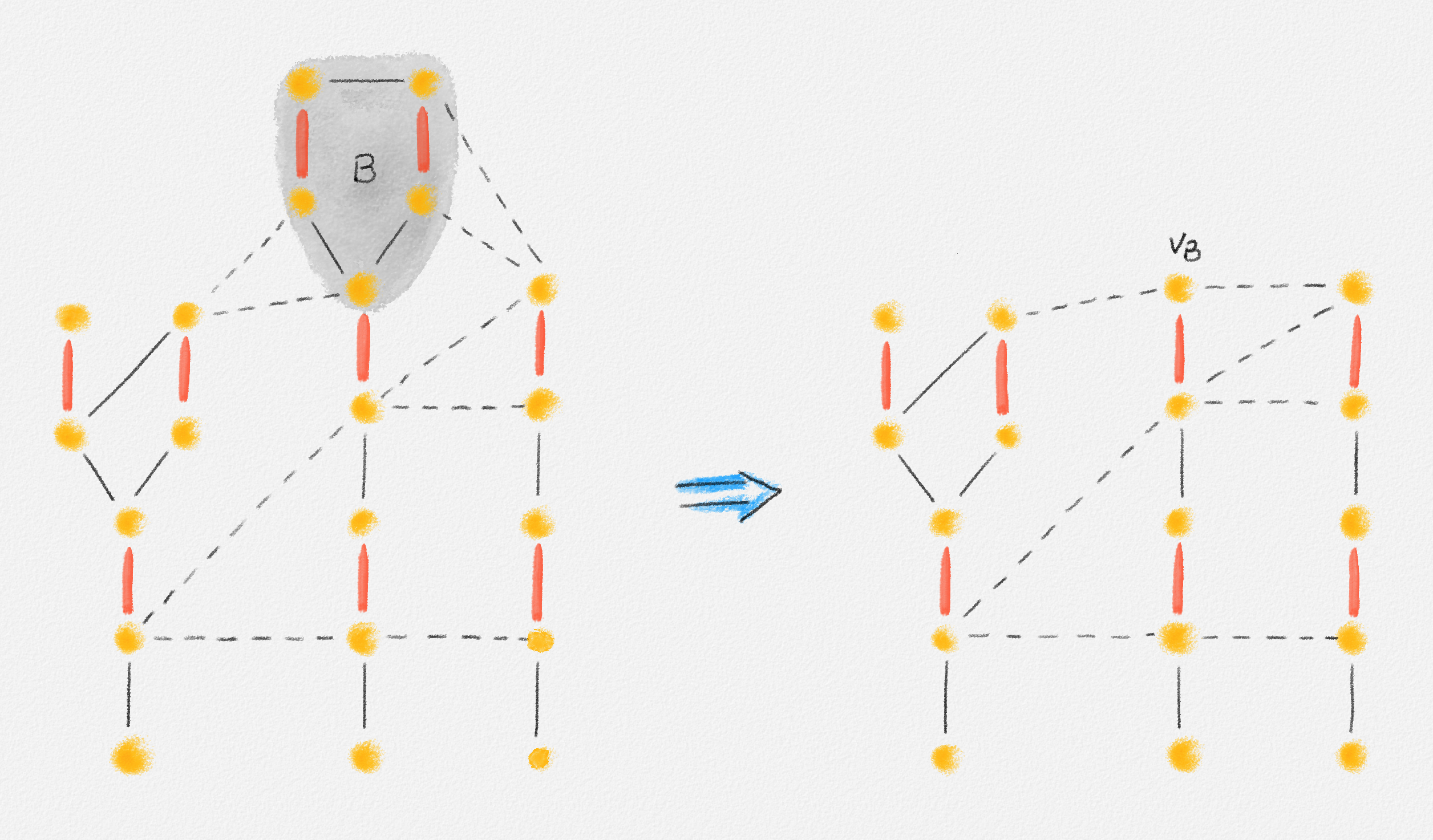
Figure 7.21: Contracting the blossom \(B\) creates a new vertex \(v_B\). Every edge with exactly one endpoint in \(B\) is now incident to \(v_B\). Duplicate edges are removed. Each edge in \(G/B\) is matched (red) if its corresponding edge in \(G\) is matched. Edges in the alternating forest are drawn solid. Edges not in the alternating forest are drawn dashed.
We also construct a matching \(M/B\) of \(G/B\), which is obtained from \(M\) by removing all those edges from \(M\) that belong to \(B\). If there is an edge \((v, w) \in M\) with exactly one endpoint in \(B\), say \(w\), then we add the edge \((v, v_B)\) to \(M/B\). Note that there can be at most one such edge in \(M\) and \(w = z\) in this case because any other vertex in \(B\) is matched by an edge in \(B\).
As we show in the next section, \(M\) is a maximum matching of \(G\) if and only if \(M/B\) is a maximum matching of \(G/B\). Thus, the algorithm recurses on \(G/B\) and \(M/B\) to try to find an augmenting path for \(M/B\) in \(G/B\). If it fails to find such a path, then \(M/B\) is a maximum matching of \(G/B\), so \(M\) is a maximum matching of \(G\) and we report that there is no augmenting path for \(M\) in \(G\). If we do find an augmenting path \(P\), then the next section also shows how to construct an augmenting path for \(M\) in \(G\) from \(P\). We construct this path and return it.
-
This is the entire algorithm for finding an augmenting path for \(M\) in \(G\) or deciding that no such path exists. Its correctness follows from the discussion above and from the results in the next subsection. To analyze its running time, observe that we can find the alternating forest \(F\) in \(O(n + m) = O(m)\) time using alternating BFS. Inspecting all edges to check whether there exists an unmatched edge \((x, y) \notin F\) such that both \(x\) and \(y\) are even takes \(O(m)\) time. Tracing the two paths \(P_x\) and \(P_y\) to identify \(r_x\) and \(r_y\), check whether \(r_x = r_y\), and construct the augmenting path \(P\) if \(r_x \ne r_y\) takes \(O(m)\) time. If \(r_x = r_y\), we need to construct \(G/B\) and \(M/B\). I leave it as an exercise to verify that this construction takes \(O(m)\) time. As we show in the next section, given an augmenting path \(P\) for \(M/B\) in \(G/B\), the construction of an augmenting path for \(M\) in \(G\) from \(P\) also takes \(O(m)\) time. Thus, excluding the cost of the recursive call on \(G/B\) and \(M/B\), we can find an augmenting path for \(M\) in \(G\) or decide that no such path exists in \(O(m)\) time.
To bound the cost of the recursive call, observe that every blossom has at least \(3\) vertices. Since we replace the entire blossom \(B\) with a single vertex in \(G/B\), the graph \(G/B\) has at most \(n - 2\) vertices. Since every edge in \(G/B\) represents at least one edge in \(G\), \(G/B\) has at most \(m\) edges. Thus, if \(T(n,m)\) is the running time of the algorithm on a graph with \(n\) vertices and \(m\) edges, this running time is bounded by the following recurrence relation:
\[T(n,m) \le \begin{cases} O(1) & \text{if } n < 2\\ O(m) + T(n - 2, m) & \text{if } n \ge 2. \end{cases}\]
(On a graph with less than two vertices, we can immediately return because the empty matching is a maximum-cardinality matching for such a graph.)
The solution of this recurrence is \(T(n,m) = O(nm)\). You should be able to prove this using substitution, which you learned in CSCI 3110.
Thus, we have the desired result:
Lemma 7.32: Given a connected graph \(G\) and a matching \(M\) of \(G\), it takes \(O(nm)\) time to find an augmenting path for \(M\) in \(G\) or decide that no such path exists.

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.