7.7.1.3. An Example

The recursive approach to finding an augmenting path for a matching \(M\) in a connected graph \(G\) may seem convoluted. To hopefully help you understand this procedure better, here is an extended example that shows how Edmonds's algorithm finds an augmenting path.

As an input, we use the graph and matching in Figure 7.26.

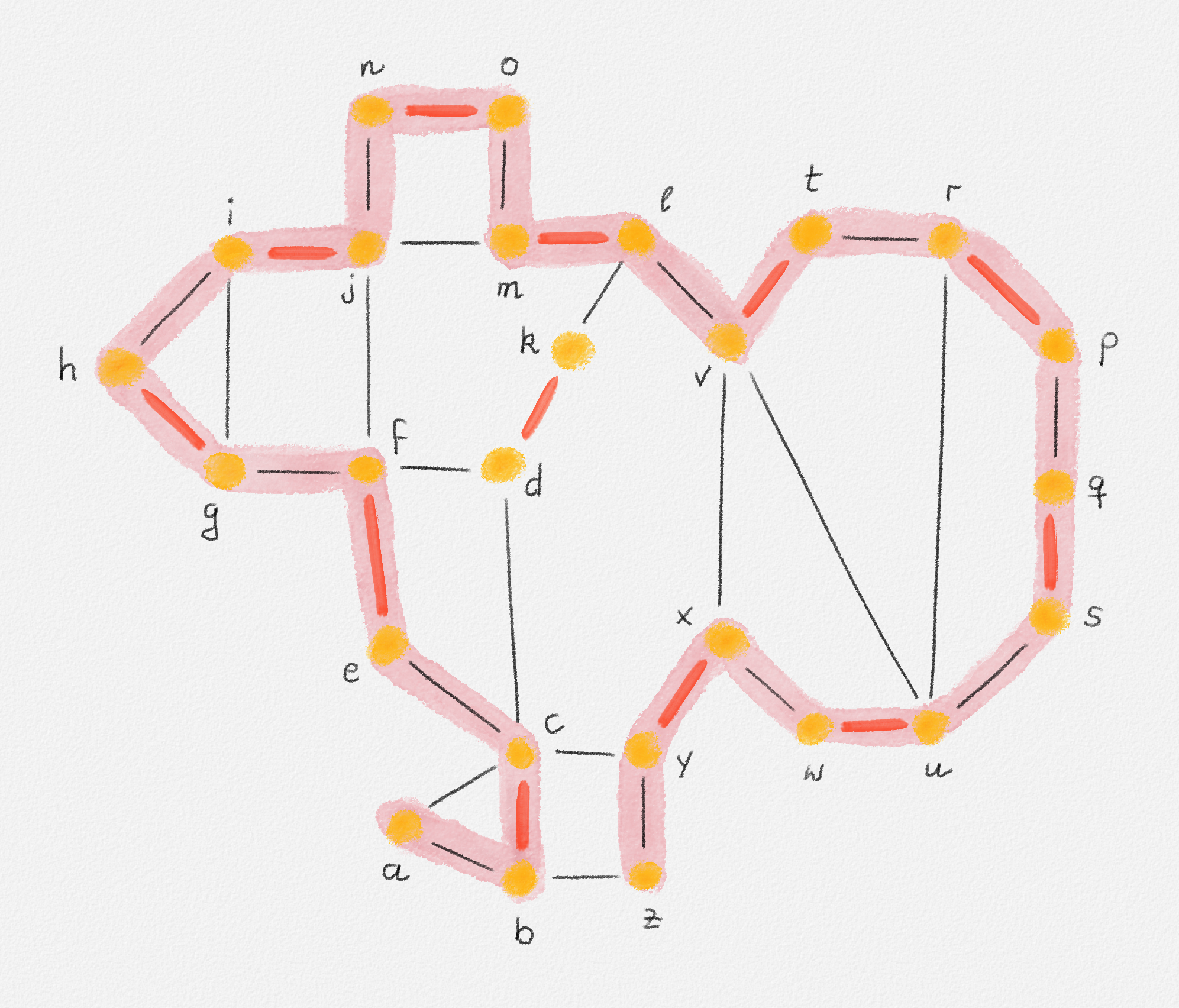
Figure 7.26: A graph \(G\) and a matching \(M\) (red edges). The matching is not maximum, as witnessed by the pink augmenting path.

We discuss how Edmonds's algorithm goes about finding the pink augmenting path in the figure (see Figure 7.27):

• We start by constructing an alternating forest of \(G\), shown in the top left of Figure 7.27. Upon detecting the edge \((h, i)\) connecting two even vertices, we contract the blossom \(B_1\) with vertex set \(\{ f, g, h, i, j\}\). This gives the graph \(G_1 = G/B_1\) along with a matching \(M_1 = M/B_1\) shown in the second figure in the top row. Note the vertex \(v_{B_1}\) representing the blossom \(B_1\) in \(G_1\).

• Next we call the algorithm recursively on \((G_1, M_1)\) in an attempt to find an augmenting path for \(M_1\) in \(G_1\). Once again, we start by constructing an alternating forest of \(G_1\). Upon detecting the edge \((m,o)\) connecting two even vertices,we construct the blossom \(B_2\) with vertex set \(\{c, d, e, k, l, m, n, o, v_{B_1}\}\). This gives the graph \(G_2 = G_1/B_2\) along with a matching \(M_2 = M_1/B_2\) shown in the third figure in the top row. Note the vertex \(v_{B_2}\) representing the blossom \(B_2\) in \(G_2\).

• Since we contracted a blossom, we once again recurse on the resulting graph \(G_2\) and the resulting matching \(M_2\). We start by constructing an alternating forest of \(G_2\) and upon detecting the edge \((p,q)\) connecting two even vertices, we contract the blossom \(B_3\) with vertex set \(\{p, q, r, s, t, u, v, w, x\}\). This gives the top-right graph \(G_3 = G_2/B_3\) and matching \(M_3 = M_2/B_3\), where the blossom \(B_3\) has been replaced with a single vertex \(v_{B_3}\).

• And one more time: We recurse on \(G_3\) and \(M_3\). This recursive call starts by constructing an alternating forest of \(G_3\). Upon detecting the edge \((v_{B_2}, v_{B_3})\) connecting two even vertices, we have finally found an augmenting path for \(M_3\) in \(G_3\) because \(v_{B_2}\) and \(v_{B_3}\) belong to different trees in the alternating forest. The augmenting path is the path \(P_3 = \langle a, b, v_{B_2}, v_{B_3}, y, z\rangle \) shown in the bottom-right of Figure 7.27. The recursive call on \(G_3\) returns this augmenting path and the recursive call on \(G_2\) is once again the active one.

• This recursive call needs to turn \(P_3\) into an augmenting path \(P_2\) for \(M_2\) in \(G_2\). Since \(v_{B_3}\) is part of the path returned by the recursive call, we construct the path \(P_2\) by splitting \(P_3\) into the two subpaths that have \(v_{B_3}\) as one of their endpoints. These subpaths correspond to paths from \(a\) to \(v\) and from \(z\) to \(x\) in \(G_2\), shown in green in the second figure from the right. We join these two paths together using the red path \(\langle v, t, r, p, q, s, u, w, x \rangle\) shown in pink. This is an even alternating path composed of only edges in the blossom. The recursive call on \(G_2\) returns this path \(P_2\) as an augmenting path in \(G_2\) and the recursive call on \(G_1\) is once again the active one.

• This recursive call constructs an augmenting path \(P_1\) in \(G_1\) in the same fashion: We split \(P_2\) into the two subpaths before and after \(v_{B_2}\). These correspond to the two green paths in \(G_1\) from \(a\) to \(c\) and from \(z\) to \(\ell\). We join these two paths together using the path \(\langle c, e, v_{B_1}, n, o, m, \ell\rangle\) in the blossom \(B_2\). The resulting path is the augmenting path in \(G_1\), which the recursive call on \(G_1\) returns. Control now returns to the top-level invocation on \(G\).

• This invocation repeats the same process one more time: We split \(P_1\) into the two subpaths before and after \(v_{B_1}\). These paths correspond to the two green paths from \(a\) to \(f\) and from \(z\) to \(j\) shown in the bottom-left figure. We join these paths using the pink path \(\langle f, g, h, i, j \rangle\) inside the blossom \(B_1\). The result is the final augmenting path \(P\) shown in Figure 7.26.

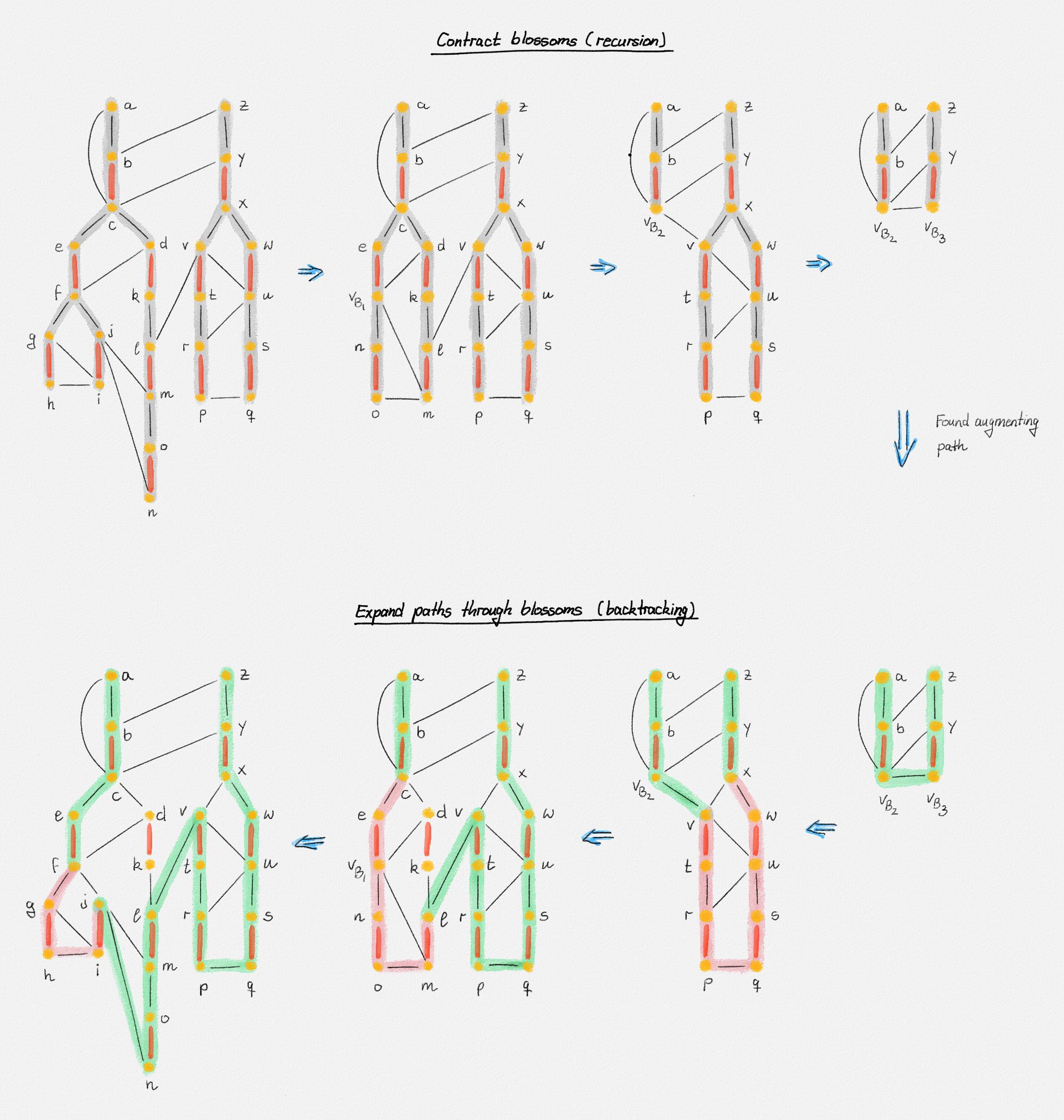
Figure 7.27: Illustration of the search for an augmenting path by Edmonds's algorithm. The top row shows, left to right, a sequence of graphs on which the algorithm recurses. The left graph is the input graph. Each subsequent graph is obtained from the previous one by contracting a blossom. The alternating forest is shown shaded. The bottom row shows how these blossoms are re-expanded after finding the augmenting path shown in the bottom-right figure. Each expansion maintains the augmenting path (green) by splitting it into the two subpath before and after \(v_{B_i}\) and then splicing these two pieces back together using an even alternating path inside the blossom (pink).