2.3.1. The Minimum Spanning Tree Problem

We have shown that the single-source shortest paths problem can be formulated as a linear program. Next let us look at a problem for which this is harder to do:

Given an edge-weighted connected undirected graph \((G,w)\), a minimum spanning tree (MST) of \((G,w)\) is a tree \(T = (V,E')\) with \(E' \subseteq E\) and such that every tree \(T' = (V,E'')\) with \(E'' \subseteq E\) satisfies \(w(E'') \ge w(E')\). See Figure 2.9.

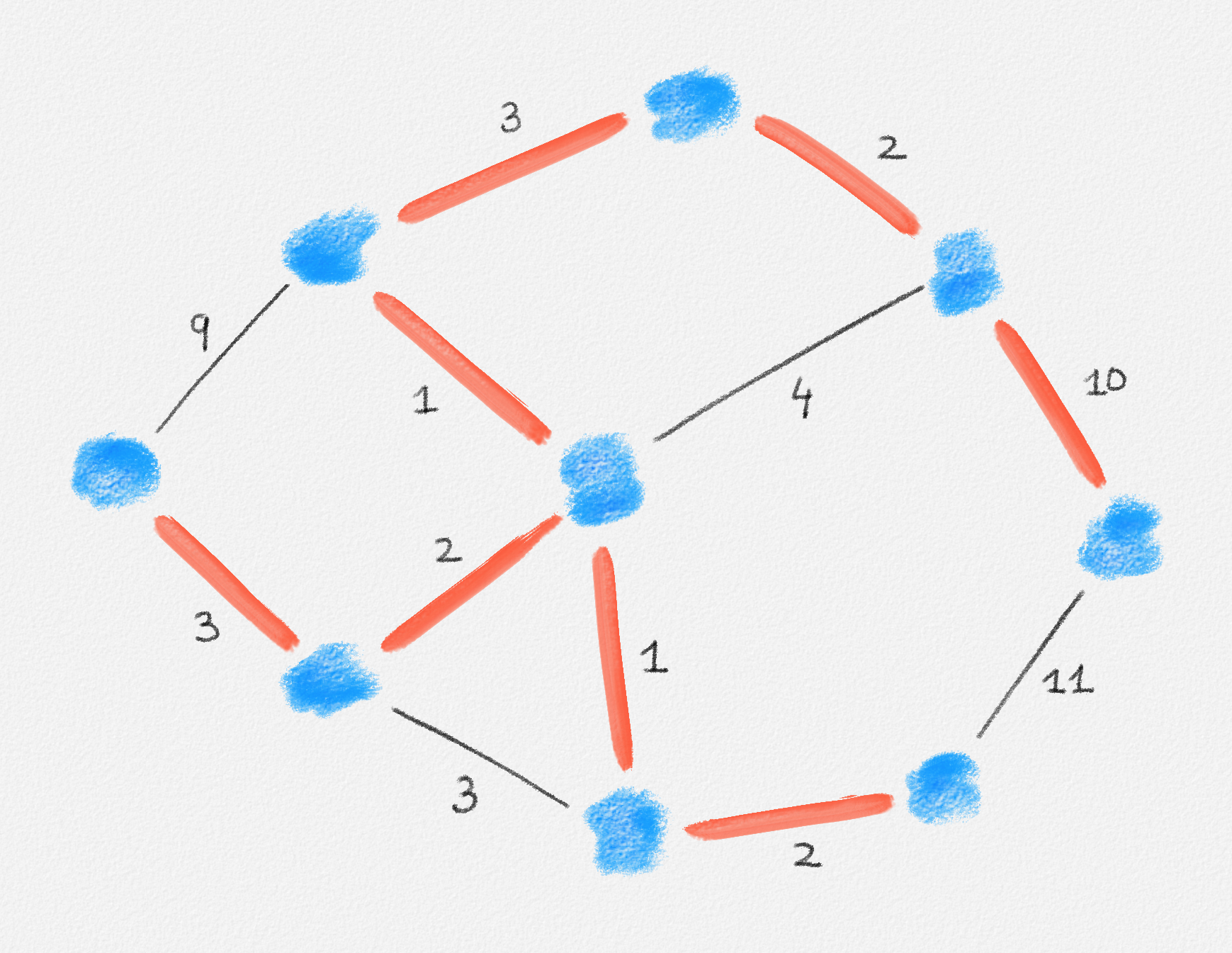
Figure 2.9: A minimum spanning tree shown in red. The edge labels are the edge weights.

Minimum spanning tree problem: For an edge-weighted graph \((G,w)\), compute a spanning tree \(T\) of \(G\) of minimum weight.