5.1.3.1. Blocking Flows

Let \(L^{f,b}\) be the residual network of \(L^f\) w.r.t. some flow \(b\) in \(L^f\).

A path \(P\) in \(L^{f,b}\) is called monotone if every edge \((x,y) \in P\) satisfies \(\mathrm{dist}_{G^f}(s,x) < \mathrm{dist}_{G^f}(s,y)\), that is, if it is an edge of \(L^f\).

A feasible \(st\)-flow \(b\) in \(L^f\) is called a blocking flow if \(L^{f,b}\) has no monotone path. See Figure 5.14.

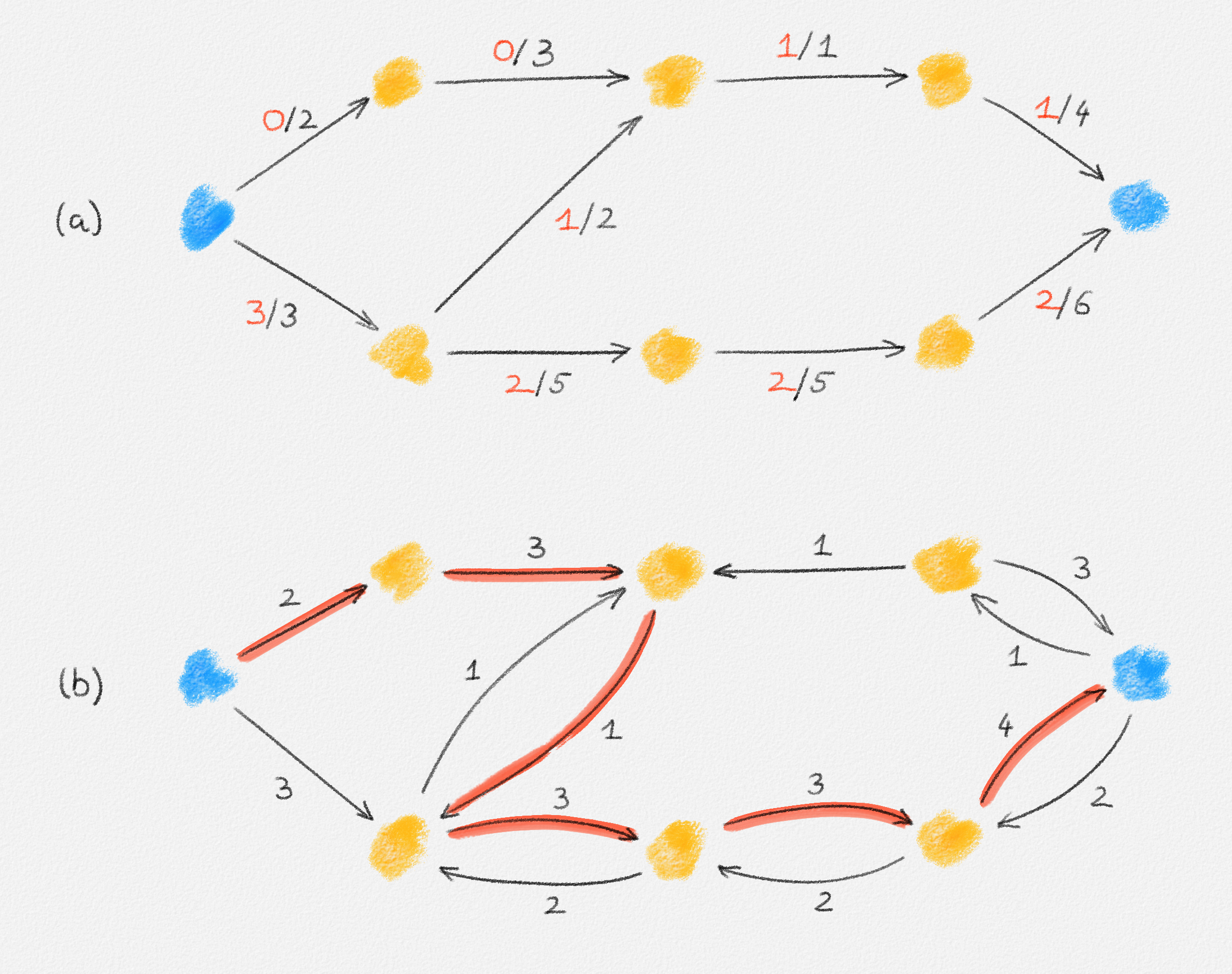
Figure 5.14: The flow represented by the red edge labels in (a) is a blocking flow. Black edge labels are capacities. While there exists an augmenting path in the residual network (b), shown in red, that path is not monotone.

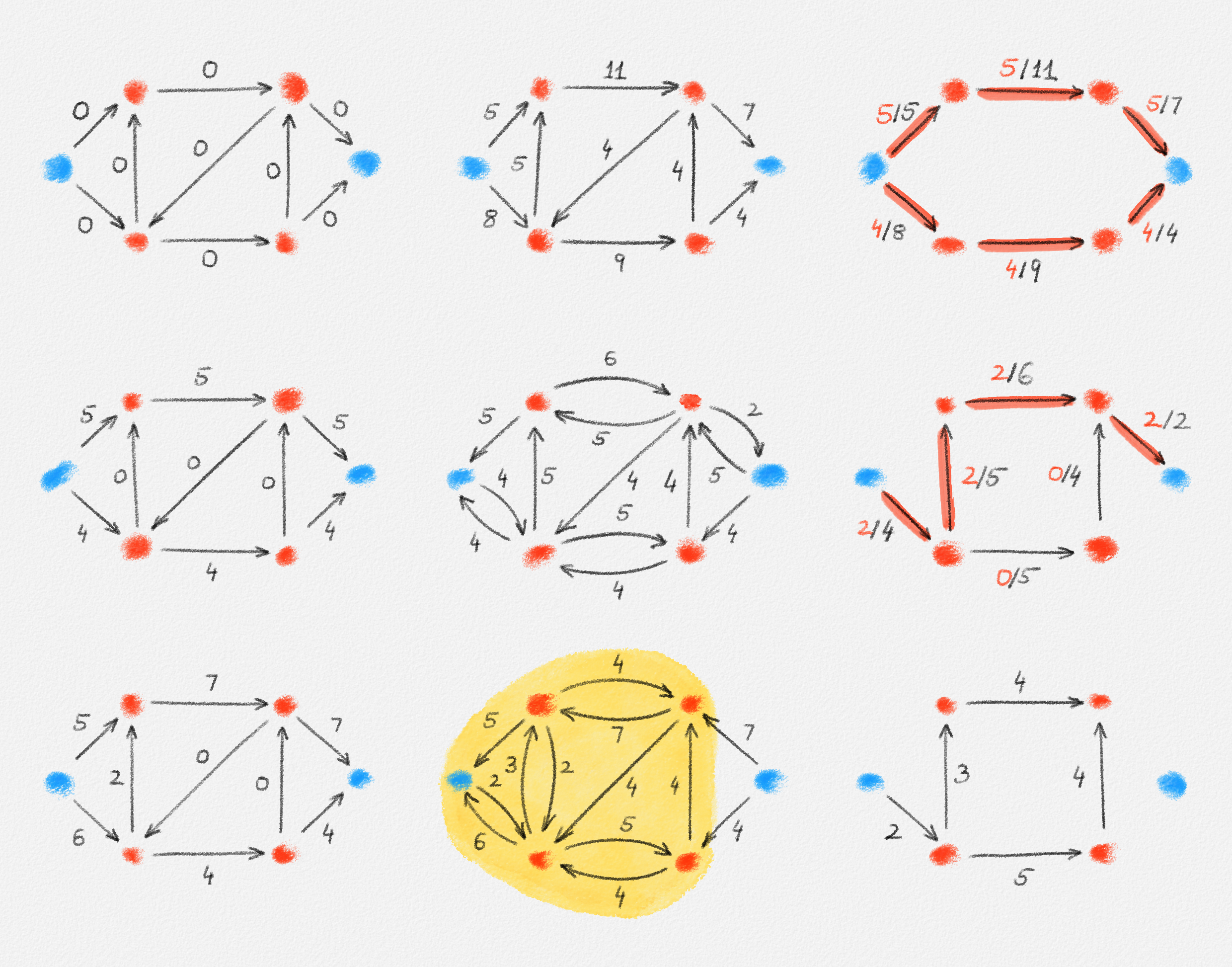
Figure 5.15: Illustration of an application of Dinitz's algorithm to the network in Figure 5.1. The edge labels in the left column show the current flow. The middle column shows the corresponding residual networks. Edge labels are residual capacities. The right column shows the level graph and a blocking flow used to augment the current flow to obtain the next flow. The red edge labels represent the blocking flow, the black edge labels the residual capacities. The last residual network contains no \(st\)-path, as illustrated by the shaded cut. This is even more visible in the level graph, which is disconnected. The corresponding flow in the bottom-left figure is thus a maximum flow in \(G\).

Lemma 5.8: Let \(b\) be a blocking flow in \(L^f\). Then the \(st\)-flow \(f'\) defined in (5.8) satisfies \(\ell^{f'} > \ell^f\).

Proof: Assume the contrary and let \(P = \langle s = x_0, \ldots, x_{\ell^{f'}} = t \rangle\) be a shortest path from \(s\) to \(t\) in \(G^{f'}\). First observe that

\[\mathrm{dist}_{G^f}(s,x_i) \le \mathrm{dist}_{G^f}(s,x_{i-1}) + 1\]

for all \(1 \le i \le \ell^{f'}\). Indeed, if there existed an index \(i\) such that

\[\mathrm{dist}_{G^f}(s,x_i) > \mathrm{dist}_{G^f}(s,x_{i-1}) + 1,\]

then this would imply that \((x_{i-1},x_i) \notin L^f\) and \((x_i,x_{i-1}) \notin L^f\). Since \(f'_{x,y} \ne f_{x,y}\) only for edges \((x,y)\) such that \((x,y) \in L^f\) or \((y,x) \in L^f\), this would imply that \(f'_{x_{i-1},x_i} = f_{x_{i-1},x_i}\) and \(f'_{x_i,x_{i-1}} = f_{x_i, x_{i-1}}\). Since \((x_{i-1},x_i) \in G^{f'}\), this would imply that \((x_{i-1},x_i) \in G^f\) and, therefore,

\[\mathrm{dist}_{G^f}(s,x_i) \le \mathrm{dist}_{G^f}(s,x_{i-1}) + 1,\]

a contradiction.

Since

\[\begin{aligned} \mathrm{dist}_{G^f}(s,x_0) &= \mathrm{dist}_{G^f}(s,s) = 0,\\ \mathrm{dist}_{G^f}\bigl(s,x_{\ell^{f'}}\bigr) &= \mathrm{dist}_{G^f}(s,t) = \ell_f,\ \text{and}\\ \mathrm{dist}_{G^f}(s,x_i) &\le \mathrm{dist}_{G^f}(s,x_{i-1}) + 1 && \forall 1 \le i \le \ell^{f'}, \end{aligned}\]

the path \(P\) has length at least \(\ell^f\).

If it includes at least one edge \((x_{i-1},x_i)\) with \(\mathrm{dist}_{G^f}(s,x_i) \le \mathrm{dist}_{G^f}(s,x_{i-1})\), its length is strictly greater than \(\ell^f\), that is, \(\ell^{f'} > \ell^f\), as claimed by the lemma.

So assume that

\[\mathrm{dist}_{G^f}(s,x_i) = \mathrm{dist}_{G^f}(s,x_{i-1}) + 1 \quad \forall 1 \le i \le \ell^{f'}.\]

Since \(f'\) is obtained from \(f\) and \(b\) using (5.8) and for every edge \((x,y) \in L^f\),

\[\mathrm{dist}_{G^f}(s,y) = \mathrm{dist}_{G^f}(s,x) + 1,\]

we have

• \(f'_{x,y} \ge f_{x,y}\) for every edge \((x,y) \in G\) with \(\mathrm{dist}_{G^f}(s,y) = \mathrm{dist}_{G^f}(s,x) + 1\),
• \(f'_{x,y} \le f_{x,y}\) for every edge \((x,y) \in G\) with \(\mathrm{dist}_{G^f}(s,y) = \mathrm{dist}_{G^f}(s,x) - 1\), and
• \(f'_{x,y} = f_{x,y}\) for any other edge.

Thus, any edge \((x,y) \in G^{f'}\) with \(\mathrm{dist}_{G^f}(s,y) = \mathrm{dist}_{G^f}(s,x) + 1\) satisfies \(u^f_{x,y} \ge u^{f'}_{x,y} > 0\), that is, the edge also belongs to \(G^f\), and hence to \(L^f\). This shows that \(P\) is a path in \(L^f\).

For every edge \((x_{i-1},x_i) \in P\), \(u^{f'}_{x_{i-1},x_i} > 0\). Also,

\[\begin{aligned} f'_{x_{i-1},x_i} &= f_{x_{i-1},x_i} + \max\bigl(0, b_{x_{i-1},x_i} - f_{x_i,x_{i-1}}\bigr)\\ f'_{x_i,x_{i-1}} &= f_{x_i,x_{i-1}} - \min\bigl(b_{x_{i-1},x_i}, f_{x_i,x_{i-1}}\bigr). \end{aligned}\]

Thus,

\[\begin{aligned} 0 &< u^{f'}_{x_{i-1},x_i}\\ &= u_{x_{i-1},x_i} - f'_{x_{i-1},x_i} + f'_{x_i,x_{i-1}}\\ &= u_{x_{i-1},x_i} - f_{x_{i-1},x_i} - \max\bigl(0, b_{x_{i-1},x_i} - f_{x_i,x_{i-1}}\bigr) + f_{x_i,x_{i-1}} - \min\bigl(b_{x_{i-1},x_i}, f_{x_i,x_{i-1}}\bigr)\\ &= u^f_{x_{i-1},x_i} - b_{x_{i-1},x_i}, \end{aligned}\]

that is,

\[b_{x_{i-1},x_i} < u^f_{x_{i-1},x_i}.\]

Since this is true for every edge \((x_{i-1},x_i) \in P\), \(P\) is a path in \(L^{f,b}\). Since \(P\) is monotone, this shows that \(b\) is not a blocking flow in \(L^f\), a contradiction. ▨

By Lemma 5.8, augmenting \(f\) using a blocking flow in each iteration of the algorithm ensures that \(\ell^f\) increases in each iteration and thus, as argued before, that the algorithm runs for at most \(n\) iterations. To achieve the desired running time of \(O\bigl(n^2m\bigr)\), it thus suffices to show how to find a blocking flow in \(O(nm)\) time. This is the final piece in the puzzle, which we discuss next.