5.1.1.3. The Max-Flow Min-Cut Theorem

Recall the definition of a cut in a graph.

An \(\boldsymbol{st}\)-cut is a cut \(S\) with \(s \in S\) and \(t \notin S\). Its capacity is

\[U_S = \sum_{x \in S, y \notin S} u_{x,y}.\]

Similarly, the flow across \(S\) is

\[F_S = \sum_{x \in S, y \notin S} \bigl(f_{x,y} - f_{y,x}\bigr).\]

These definitions are illustrated in Figure 5.10.

Figure 5.10: An \(st\)-flow in a network \(G\) and an \(st\)-cut \(S\) consisting of the vertices in the shaded region. This cut has capacity \(U_S = 16\). the flow across this cut is \(F_S = 9\).

A minimum \(\boldsymbol{st}\)-cut is an \(st\)-cut of minimum capacity.

First, it is helpful to understand how \(st\)-cuts interact with flows from \(s\) to \(t\).

Lemma 5.3: Let \(S\) be an \(st\)-cut of \(G\) and let \(f\) be a feasible \(st\)-flow in \(G\). Then \(F_s = F_S\).

Proof: The lemma follows directly from flow conservation:

\[\begin{aligned} F_s &= \sum_{y \in V} \bigl(f_{s,y} - f_{y,s}\bigr)\\ &= \sum_{y \in V} \bigl(f_{s,y} - f_{y,s}\bigr) + \sum_{x \in S \setminus \{s\}}\sum_{y \in V} \bigl(f_{x,y} - f_{y,x}\bigr) \end{aligned}\]

because \(\sum_{y \in V} \bigl(f_{x,y} - f_{y,x}\bigr) = 0\) for all \(x \in S \setminus \{s\}\) due to flow conservation (\(x\) is neither \(s\), because \(x \in S \setminus \{s\}\), nor \(t\), because \(t \notin S\)). Thus,

\begin{align} F_s &= \sum_{x \in S} \sum_{y \in V} \bigl(f_{x,y} - f_{y,x}\bigr)\\ &= \sum_{x \in S} \sum_{y \in S} \bigl(f_{x,y} - f_{y,x}\bigr) + \sum_{x \in S} \sum_{y \notin S} \bigl(f_{x,y} - f_{y,x}\bigr).\tag{5.2} \end{align}

The first sum in (5.2) is \(0\) because every edge flow \(f_{x,y}\) with \(x, y \in S\) occurs twice in this sum, once with positive sign and once with negative sign. The second sum is \(F_S\). Thus, \(F_s = F_S\). ▨

The next theorem is a classical result that can be seen as the network flow equivalent of LP duality. Recall that Theorem 4.3 states that a feasible solution of an LP and a feasible solution of its dual LP are optimal solutions if and only if they have the same objective function value. The following theorem establishes an analogous relationship between maximum flows and minimum cuts.

Theorem 5.4 (Max-Flow Min-Cut Theorem): Let \(f\) be a feasible \(st\)-flow in \(G\) and let \(S\) be an \(st\)-cut of \(G\). Then \(f\) is a maximum \(st\)-flow and \(S\) is a minimum \(st\)-cut if and only if \(F_s = U_S\).

This result follows immediately from LP duality after observing that the LP formulation of the minimum \(st\)-cut problem is exactly the dual of the LP formulation of the maximum flow problem.

Exercise 5.1: Prove the Max-Flow Min-Cut Theorem by constructing the dual of the LP formulation of the maximum flow problem and showing that any feasible solution of this dual is an \(st\)-cut, and vice versa.

Here, we opt for a direct graph-theoretic proof.

Proof (Theorem 5.4): Let \(f^*\) be a maximum \(st\)-flow and let \(S^*\) be a minimum \(st\)-cut. By Lemma 5.3, we have

\[F_s \le F^*_s = F^*_{S^*} = \sum_{x \in S^*, y \notin S^*} \bigl(f^*_{x,y} - f^*_{y,x}\bigr) \le \sum_{x \in S^*, y \notin S^*} f^*_{x,y} \le \sum_{x \in S^*, y \notin S^*} u_{x,y} = U_{S^*} \le U_S.\]

Thus, if \(F_s = U_S\), then \(F_s = F^*_s = U_{S^*} = U_S\), that is, \(f\) is a maximum \(st\)-flow (\(F_s = F^*_s\)) and \(S\) is a minimum \(st\)-cut (\(U_{S^*} = U_S\)).

Conversely, assume that \(f\) is a maximum \(st\)-flow and \(S\) is a minimum \(st\)-cut. By Observation 5.2, there exists no augmenting \(st\)-path in \(G^f\). Thus, if we choose \(S'\) to be the set of all vertices reachable from \(s\) in \(G^f\), then \(s \in S'\) and \(t \notin S'\), that is, \(S'\) is an \(st\)-cut. See Figure 5.11.

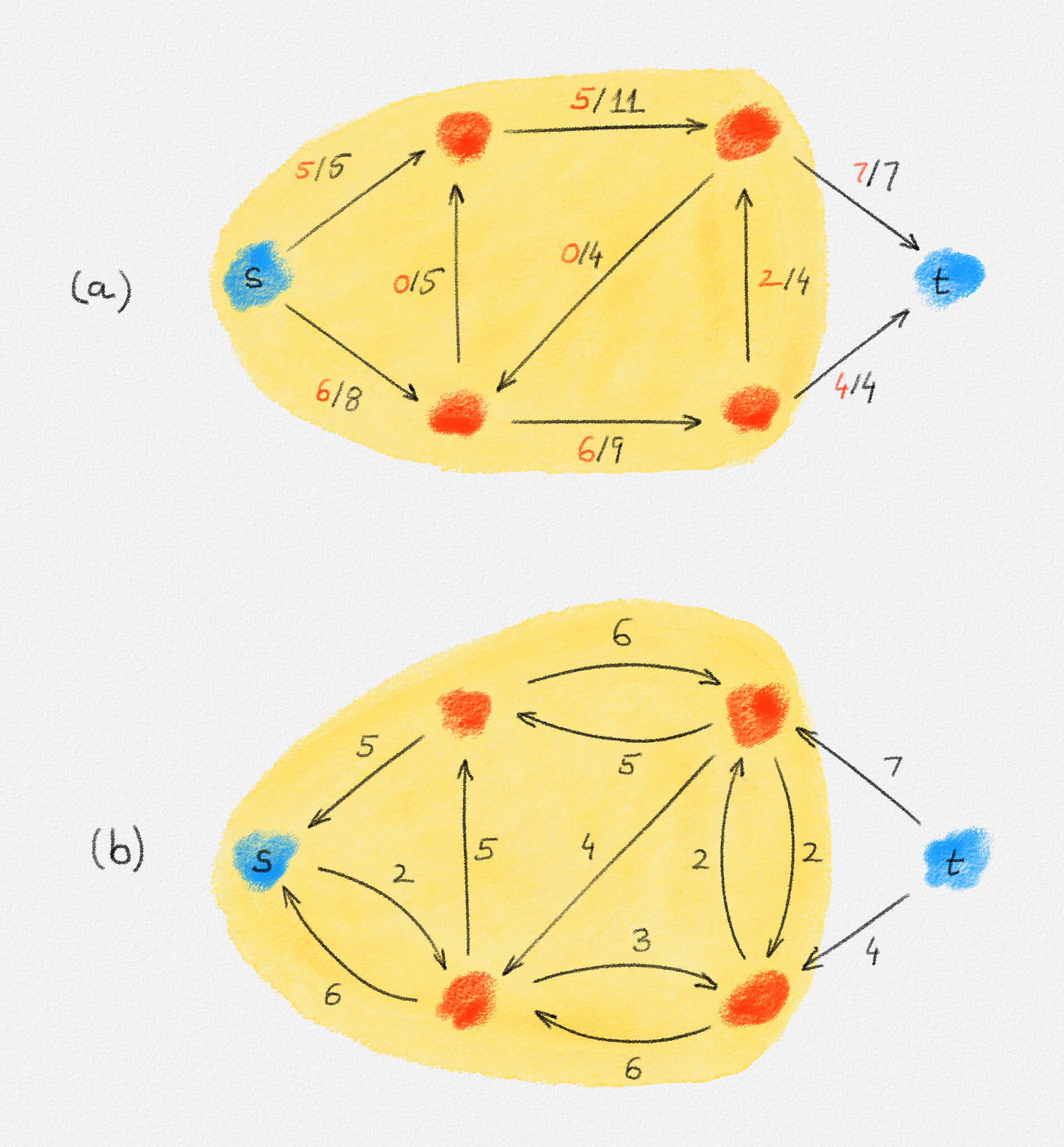
Figure 5.11: (a) A maximum flow \(f\) and a minimum cut \(S\) (shaded) that satisfy \(F_s = F_S = U_S = 11\). (b) The residual network \(G^f\). \(S\) is the set of vertices reachable from \(s\) in \(G^f\).

Since \(S\) is a minimum \(st\)-cut, we have \(F_s \le U_S \le U_{S'}\). We prove that \(F_s = U_{S'}\). Thus, \(F_s = U_S = U_{S'}\).

For every edge \((x,y) \in E\) with \(x \in S'\) and \(y \notin S'\), \(f_{x,y} = u_{x,y}\) because otherwise, the edge \((x,y)\) would be an edge of \(G^f\) and thus, since \(x \in S'\), \(y\) would also be in \(S'\). Similarly, if \(x \notin S'\) and \(y \in S'\), then \(f_{x,y} = 0\) because otherwise, the edge \((y,x)\) would belong to \(G^f\) and thus \(x \in S'\). Thus,

\[F_s = F_{S'} = \sum_{x \in S', y \notin S'} \bigl(f_{x,y} - f_{y,x}\bigr) = \sum_{x \in S', y \notin S'} u_{x,y} = U_{S'}. \text{▨}\]

The correctness of the Ford-Fulkerson algorithm now follows from the following argument: By Lemma 5.1, each iteration of the algorithm maintains that \(f\) is a feasible flow. Once the algorithm terminates, there is no more augmenting path. As in the proof of the Theorem 5.4, this implies that there exists an \(st\)-cut in \(G\) whose capacity equals \(F_s\) and, hence, \(f\) is a maximum \(st\)-flow.

What is left is to figure out an appropriate strategy to find augmenting paths that guarantees that the algorithm terminates, and hopefully quickly.