5.1.1.1. Ford-Fulkerson May Not Terminate
The following example shows that, if the augmenting path is not chosen carefully in each iteration, then the MaxFlow procedure may not terminate and the flow value it converges to may be far from the value of a maximum flow:
Consider the network in Figure 5.5, where \(\rho = \frac{\sqrt{5}- 1}{2}\) and \(X > 2\).
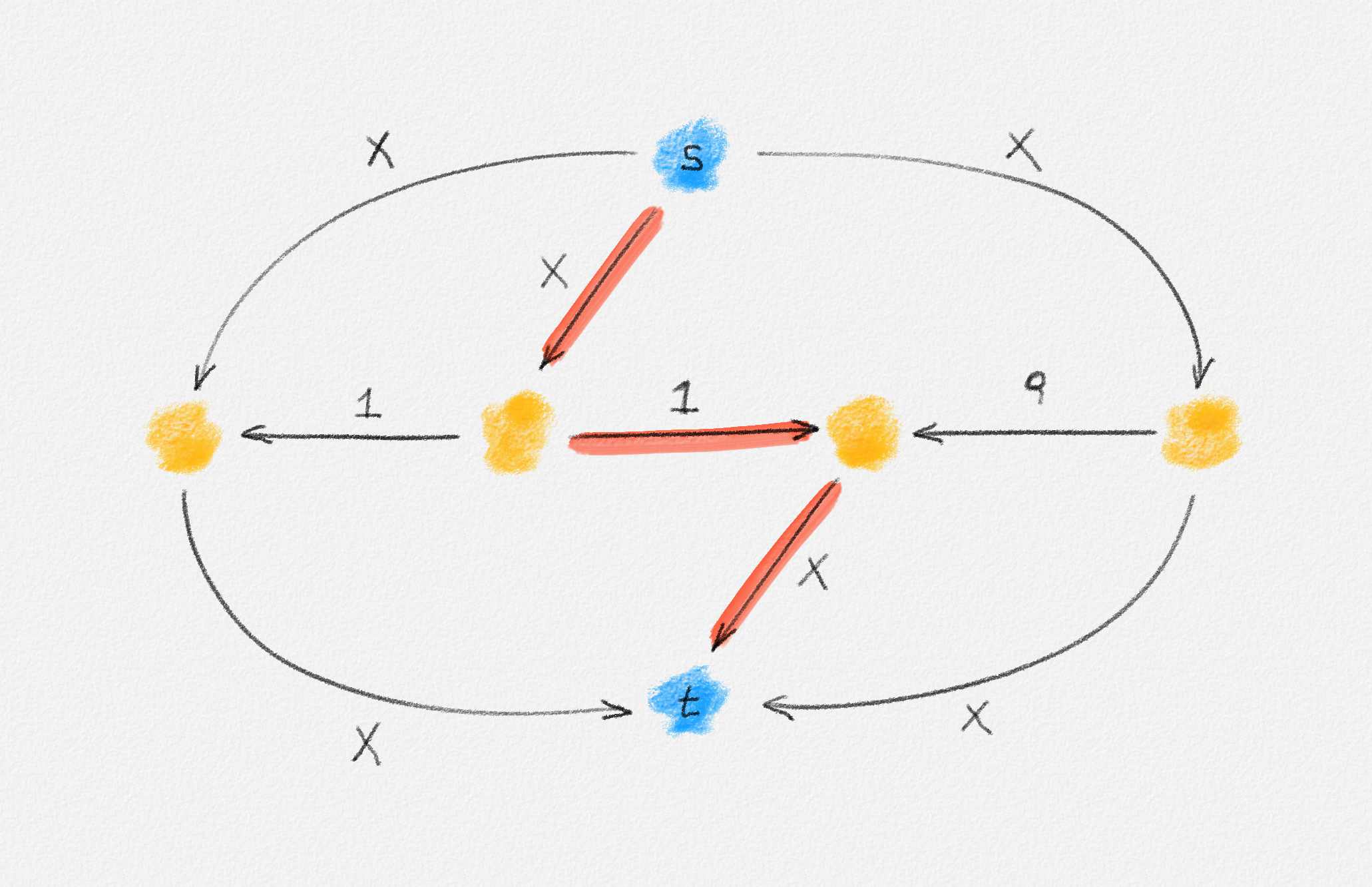
In the first augmentation, the algorithm may push one unit of flow along the red path, which leaves the residual network shown in Figure 5.6, for \(i = 1\).
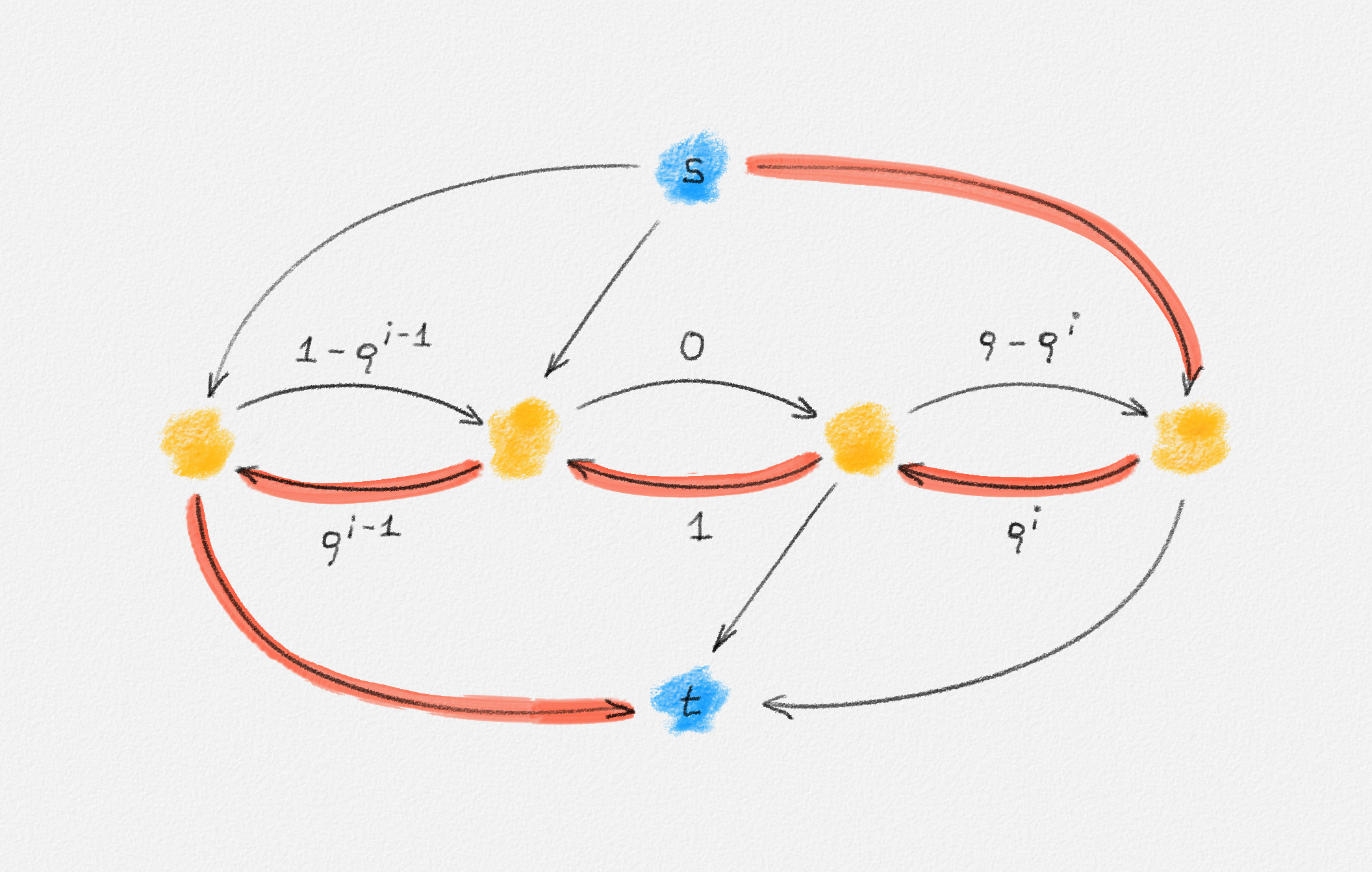
The capacities of the edges incident to \(s\) or \(t\) are not shown because \(X\) is large enough that these edges do not determine the capacity of any augmenting path used in this example.
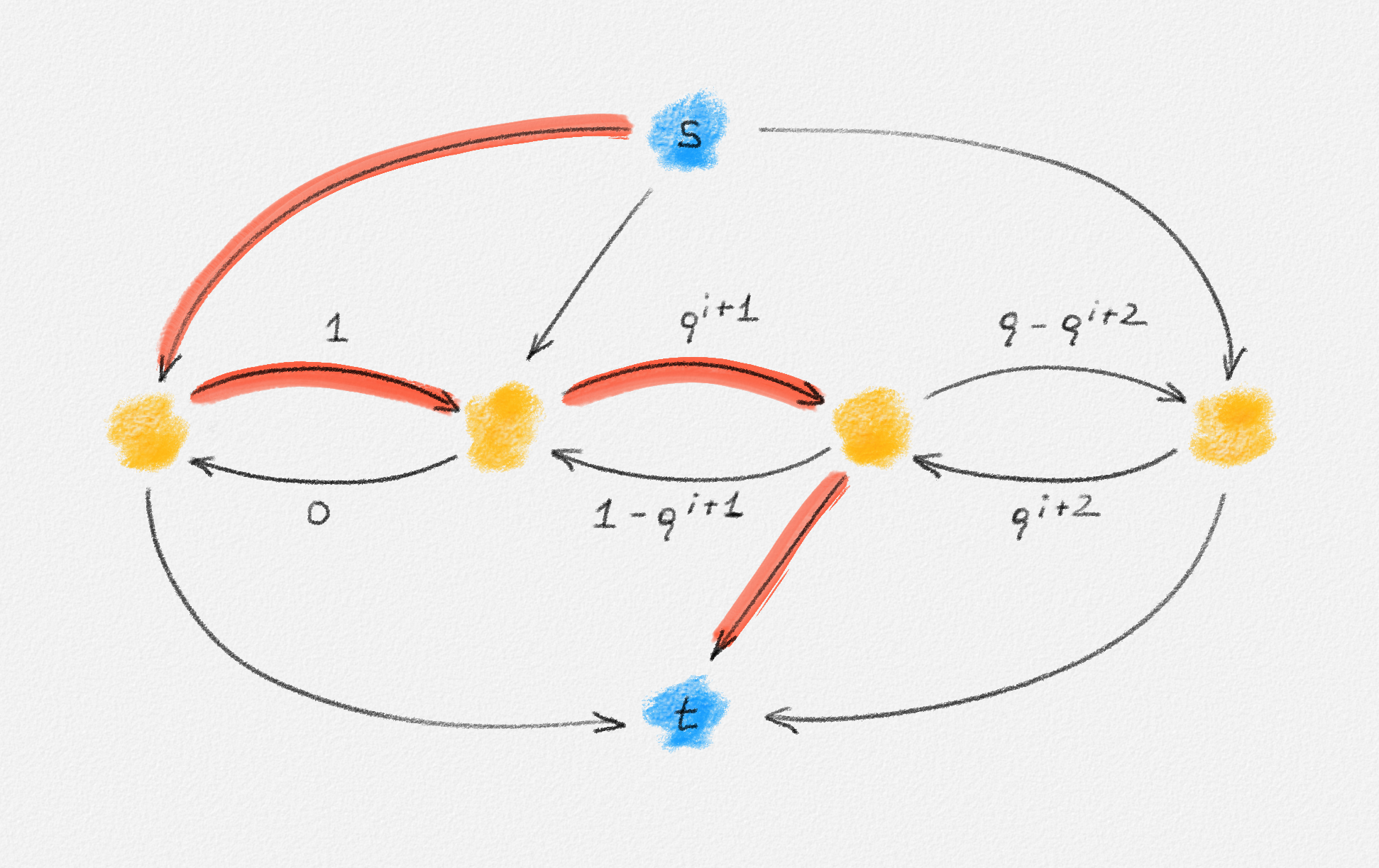
Given the residual network in Figure 5.6 for some value \(i\), the following four augmentations return to the same residual network but with the value of \(i\) increased by \(2\):
-
First, we push \(\rho^i\) units of flow along the red path in Figure 5.6. This produces the residual network in Figure 5.7.
-
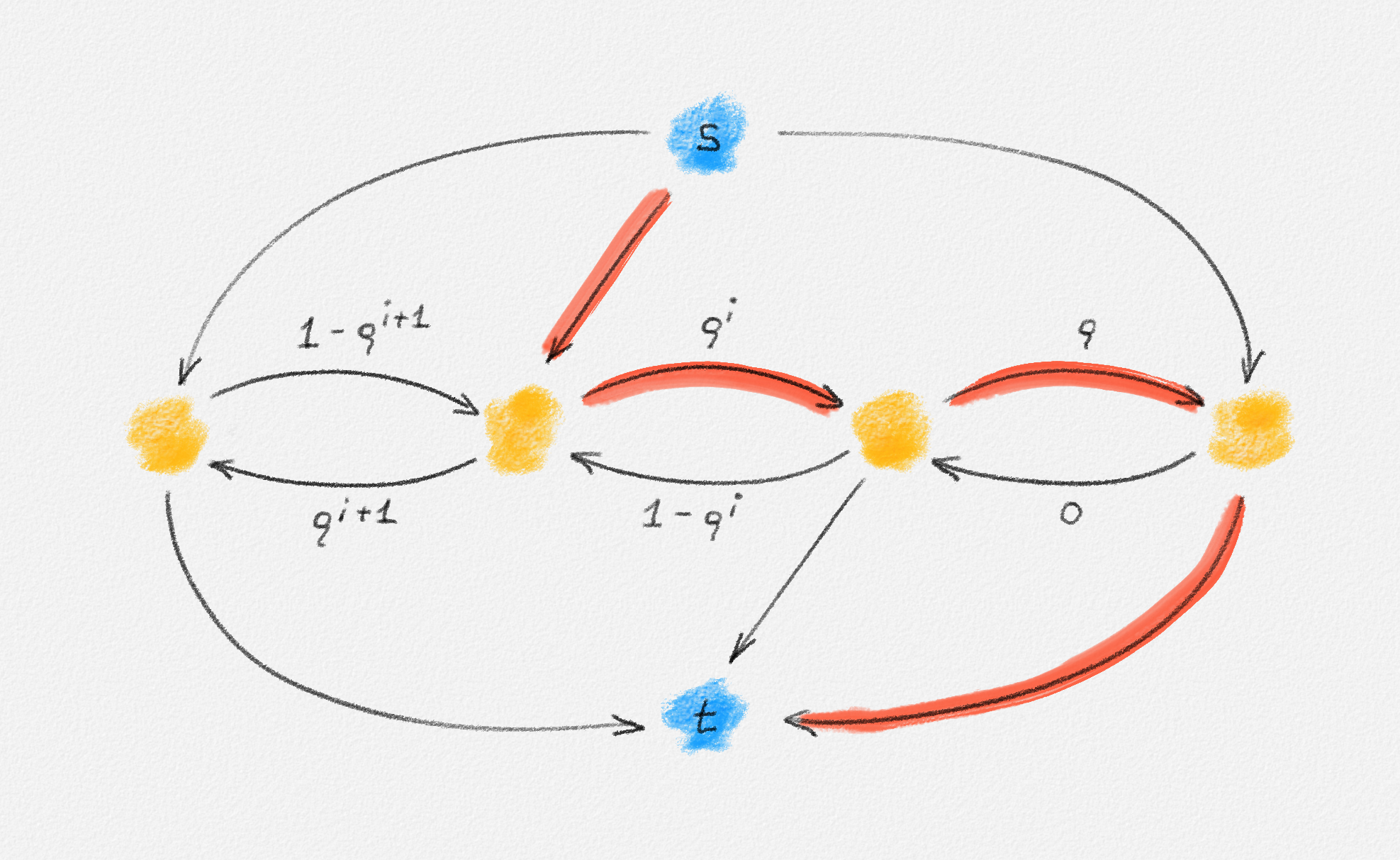
Next, we push \(\rho^i\) units of flow along the red path in Figure 5.7. This produces the residual network in Figure 5.8.
-
Next, we push \(\rho^{i+1}\) units of flow along the red path in Figure 5.8. This produces the residual network in Figure 5.9.
-
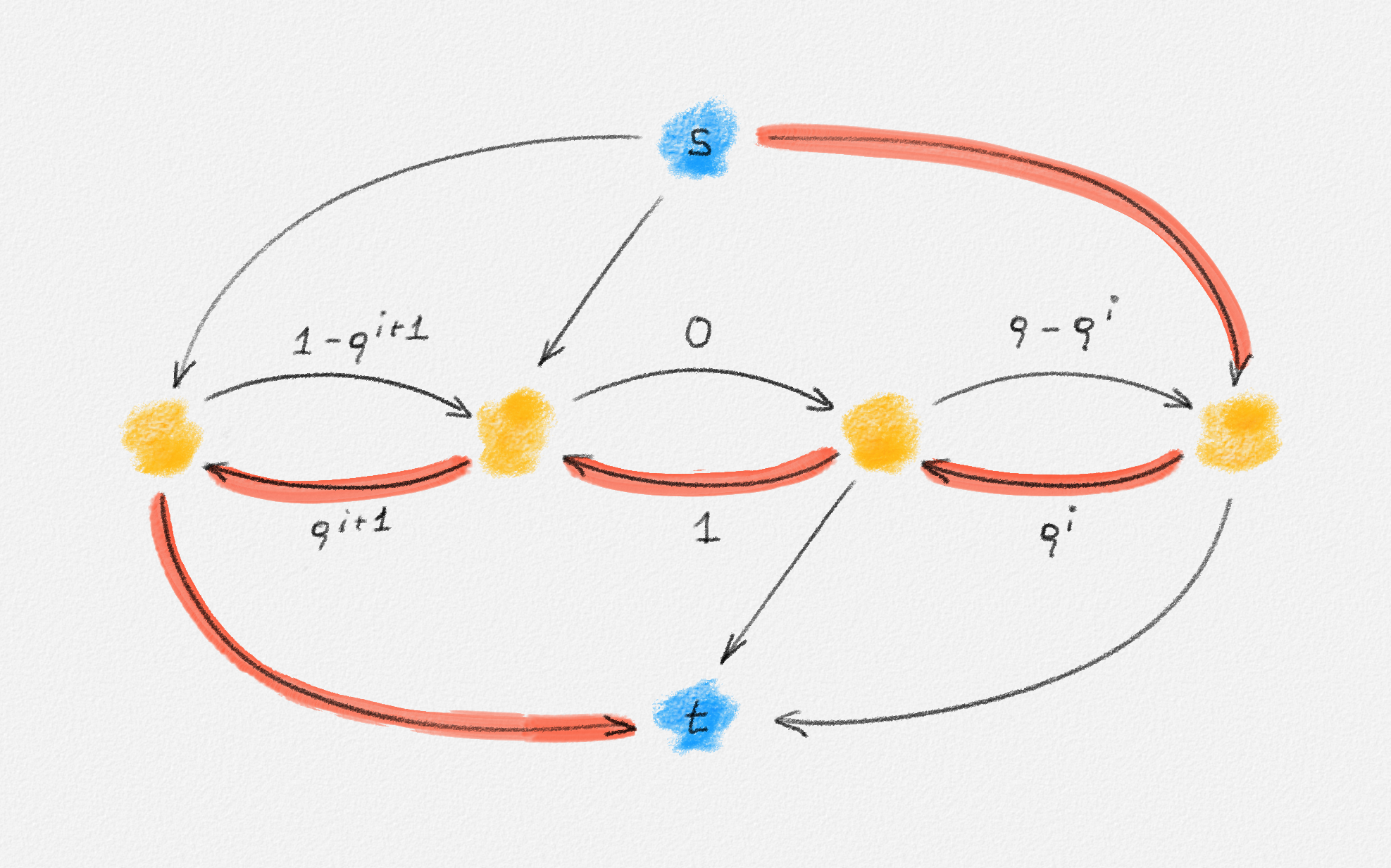
Finally, we push \(\rho^{i+1}\) units of flow along the red path in Figure 5.9. This produces the residual network in Figure 5.6 with \(i\) increased by \(2\).
The consequence is that there always exists an augmenting path from \(s\) to \(t\), so the algorithm does not terminate. The total amount of flow pushed from \(s\) to \(t\) converges to
\[1 + \sum_{i=1}^\infty 2\rho^i = \sum_{i=0}^\infty 2\rho^i - 1 = \frac{4}{3 \sqrt{5}} - 1 < 5\]
while the maximum \(st\)-flow clearly has value \(2X + 1 > 5\). By using a large value of \(X\), the gap between the maximum \(st\)-flow and the limit of the \(st\)-flows produced by the algorithm can be made arbitrarily large.

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.