5.2.1. The Generic Preflow-Push Algorithm

Here is another useful metaphor that can be used to understand preflow-push algorithms and which translates directly into how these algorithms operate: Assume that \(s\) initially holds \(\sum_{y \in V} u_{s,y}\) units of flow (litres of water). We can make this water flow to \(s\)'s neighbours by raising \(s\) so it is higher than its neighbours and the water flows downhill to \(s\)'s neighbours. We raise \(s\) and its neighbours further to make the water flow further to the vertices two hops away from \(s\), and so on. At some point, \(t\) is the lowest vertex and some of the water reaches \(t\) while some water may be stuck at intermediate vertices (because their out-edges are at capacity). By lifting up vertices so they are higher than \(s\), we make this excess water flow back to \(s\).

Formally, every vertex is given a height \(h_x\). The height of \(s\) is fixed at \(h_s = n\) while the algorithm runs. Similarly, the height of \(t\) is held constant at \(h_t = 0\). For every other vertex \(x \notin \{s, t\}\), \(h_x = 0\) initially; over the course of the algorithm, \(h_x\) increases but never exceeds \(2n-1\).

A height function \(h : V \rightarrow \mathbb{N}\) satisfies the following conditions with respect to the current preflow \(f\):

• \(h_s = n\),
• \(h_t = 0\), and
• For every edge \((x, y) \in G^f\), \(h_x \le h_y + 1\). (Water never flows downhill too quickly.)

If \(f_{x,y} = u_{x,y}\) and \(f_{y,x} = 0\), then \((x,y) \notin G^f\). Thus, the initial height function \(h\) and preflow \(f\) satisfy this condition:

\[\begin{aligned} f_{x,y} &= \begin{cases} u_{x,y} & \text{if } x = s\\ 0 & \text{if } x \ne s. \end{cases}\\ h_x &= \begin{cases} n & \text{if } x = s\\ 0 & \text{if } x \ne s. \end{cases} \end{aligned}\]

The generic preflow-push algorithm now repeatedly applies the following operations until \(f\) is a feasible flow (see Figure 5.16):

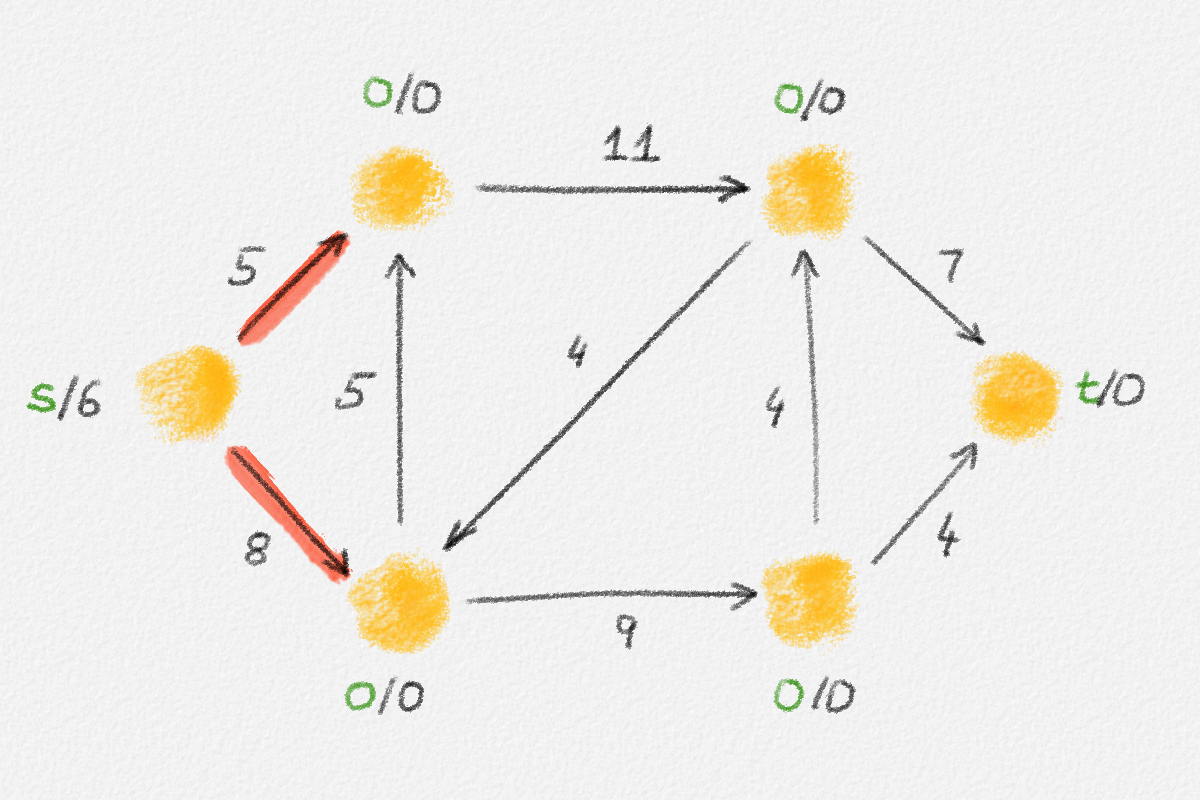
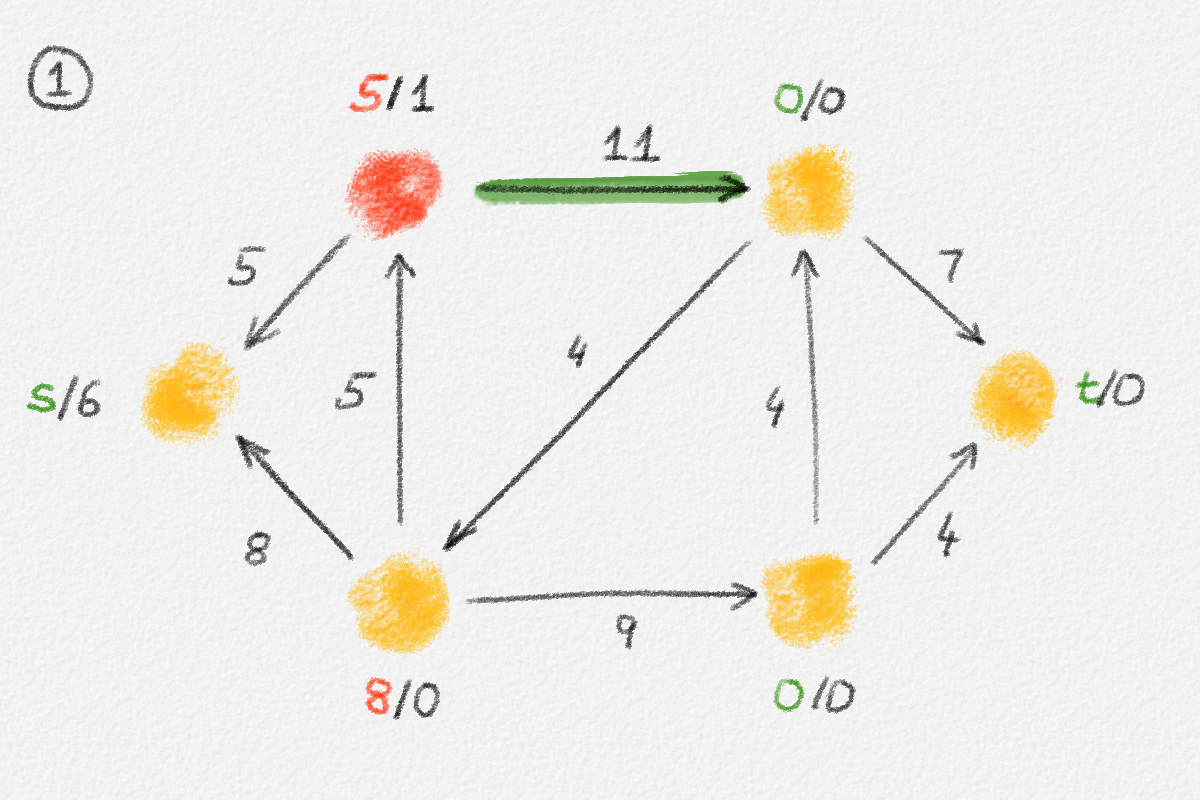
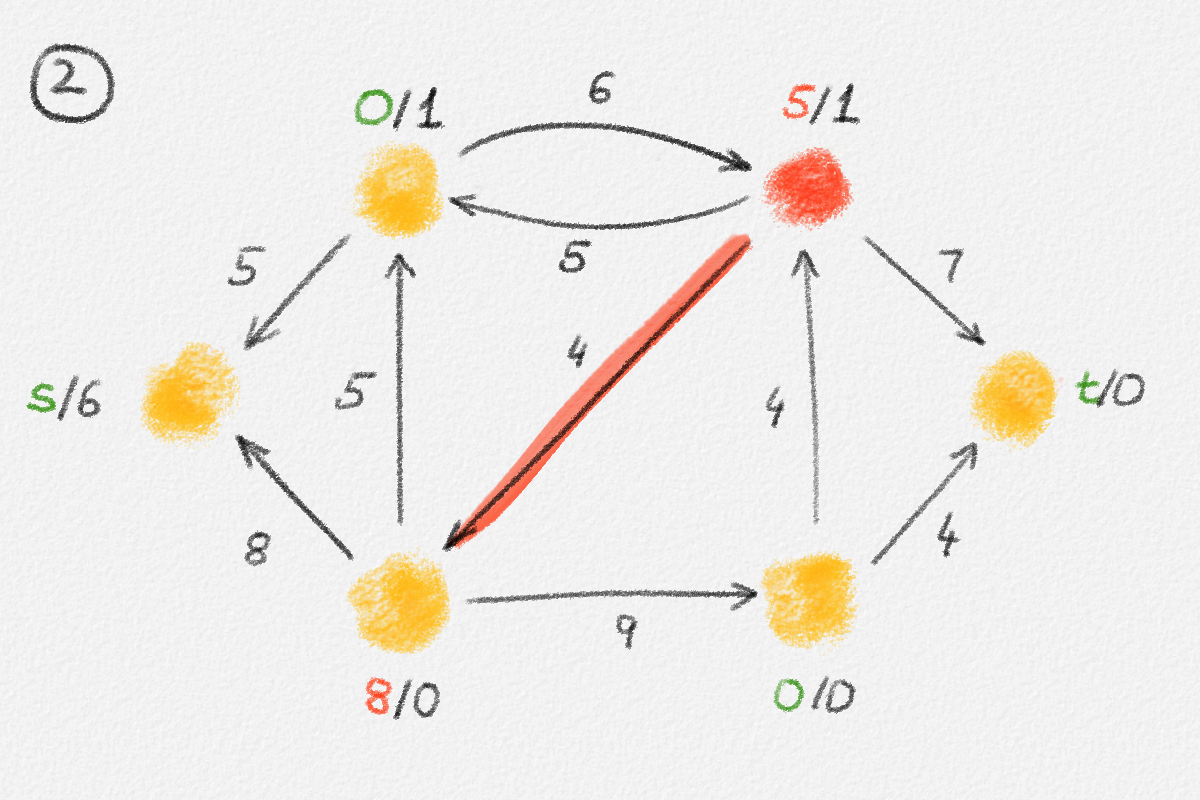
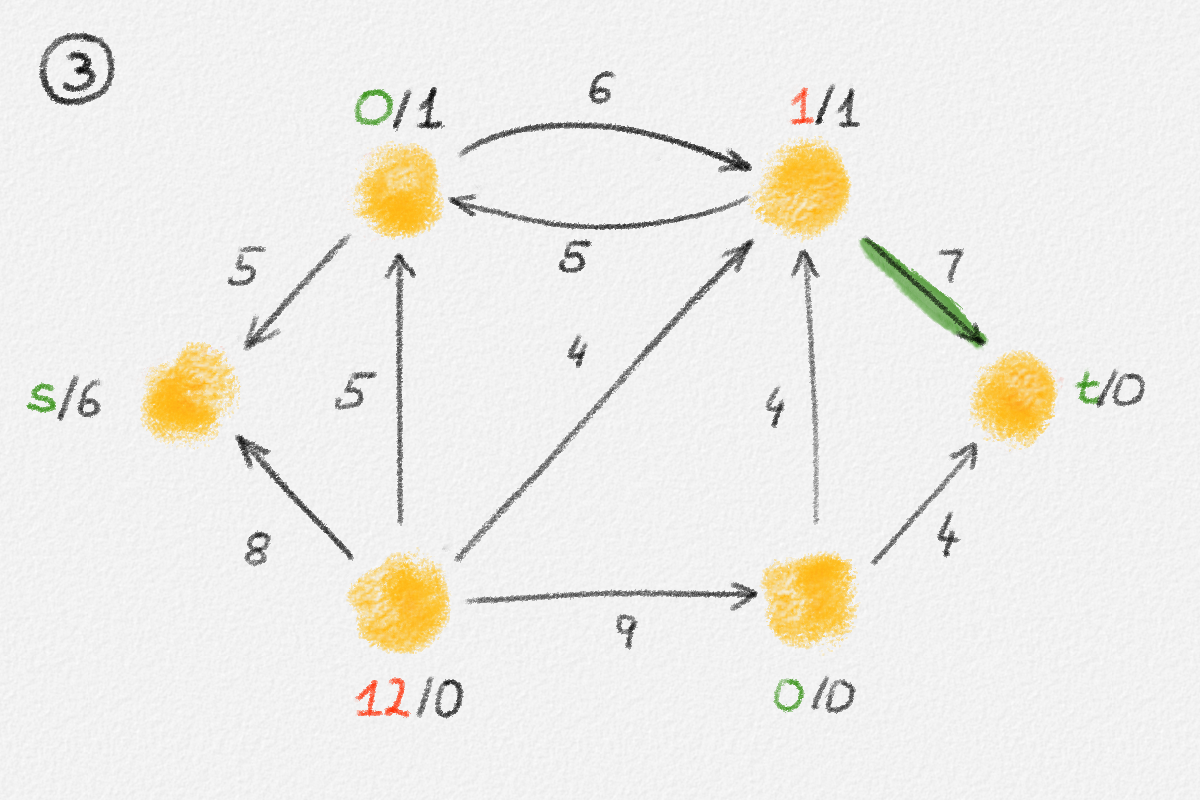
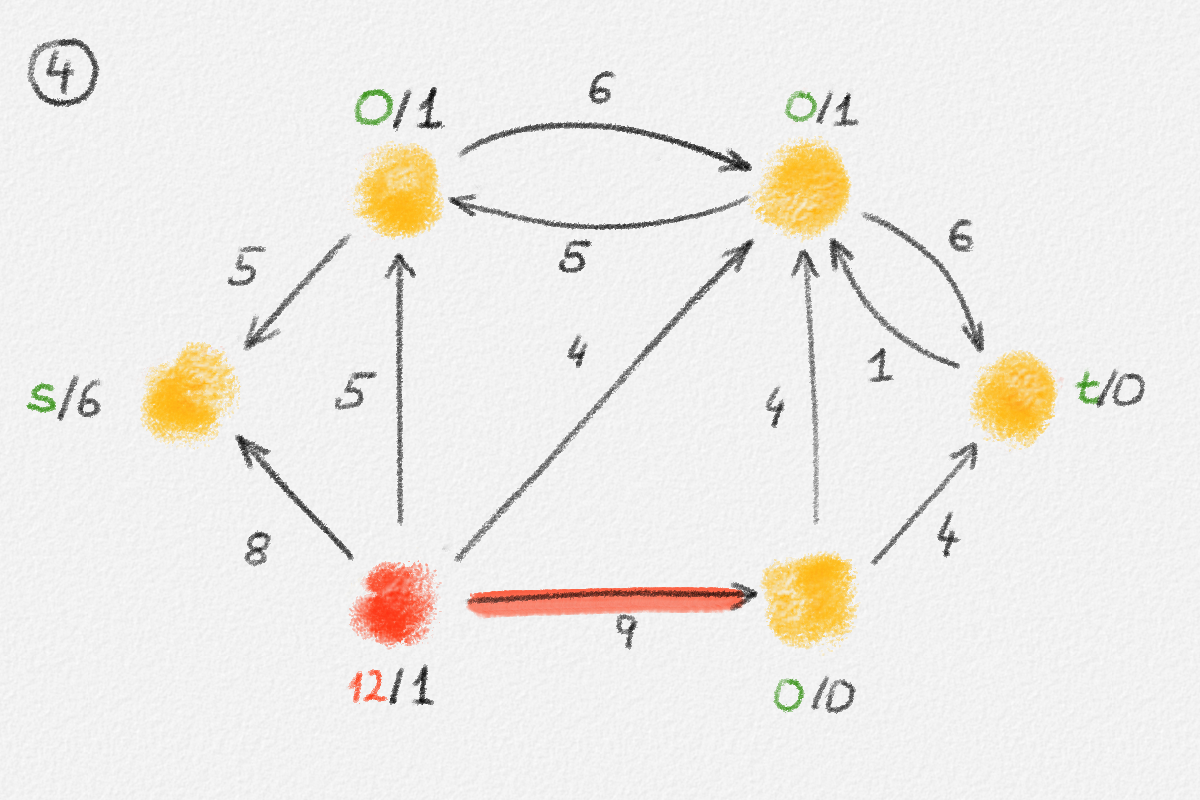
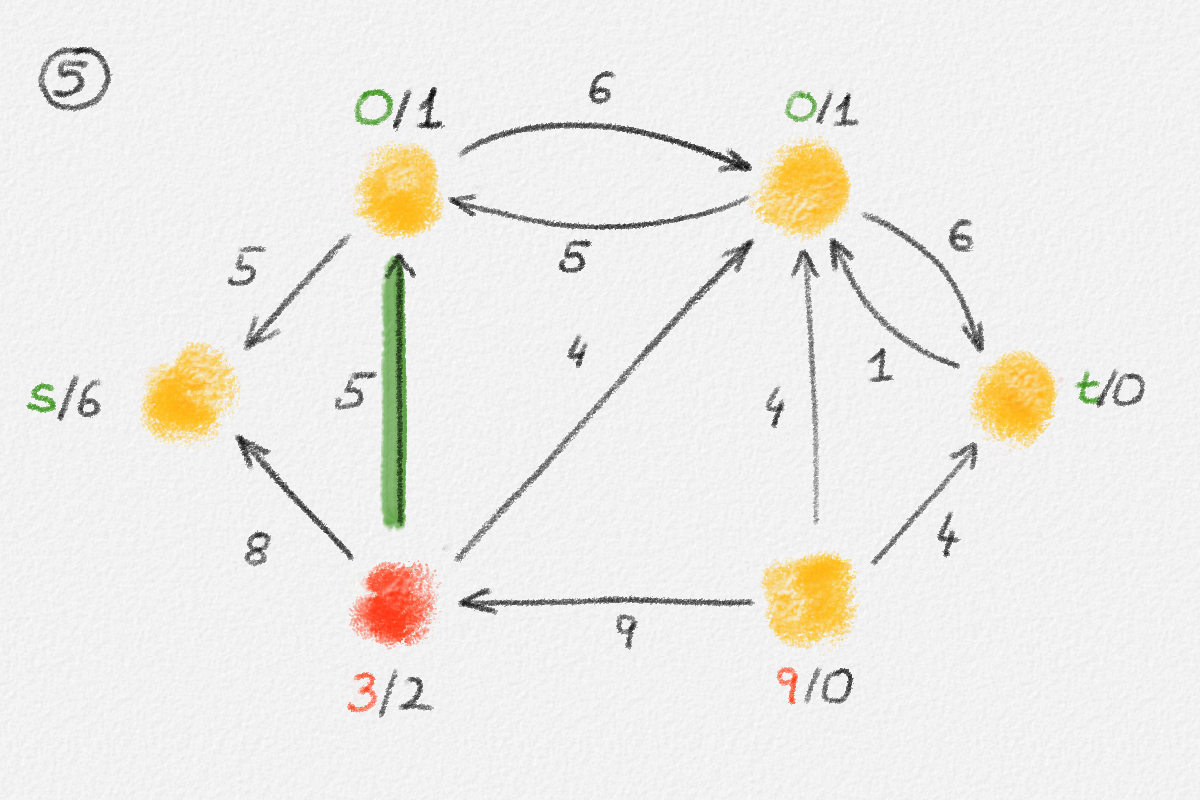
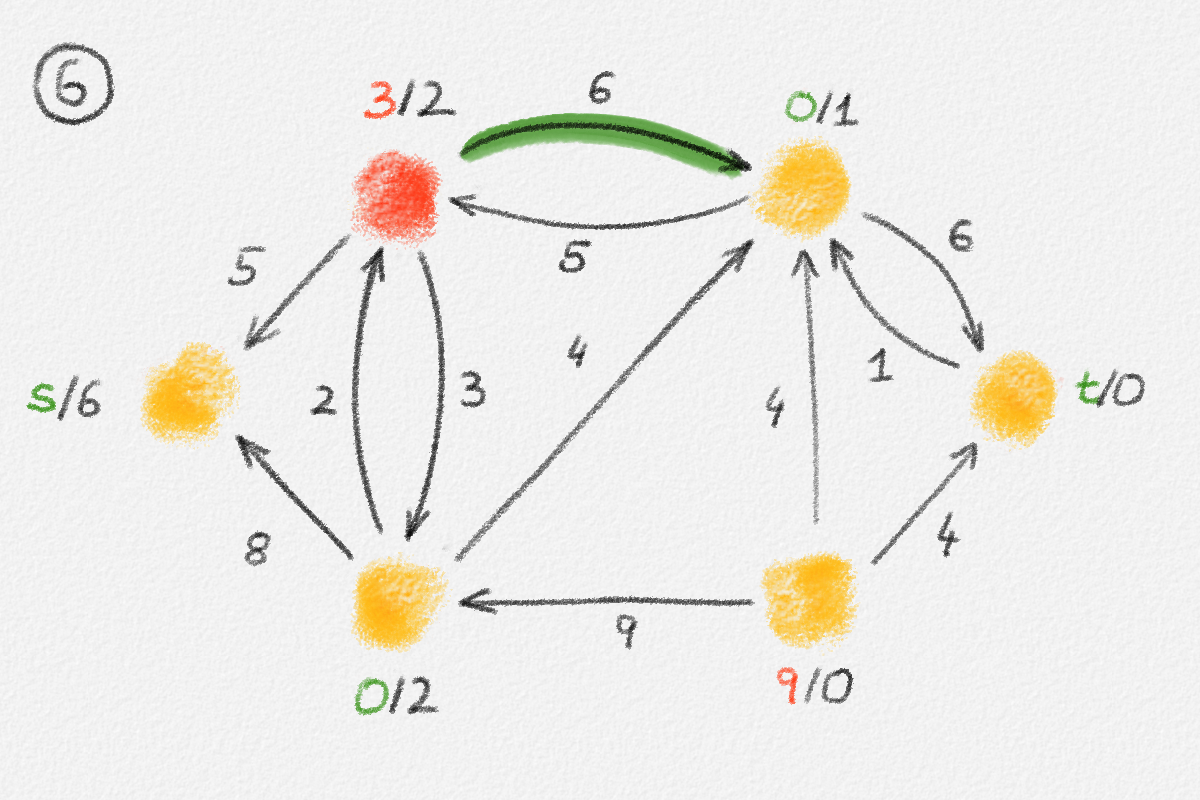
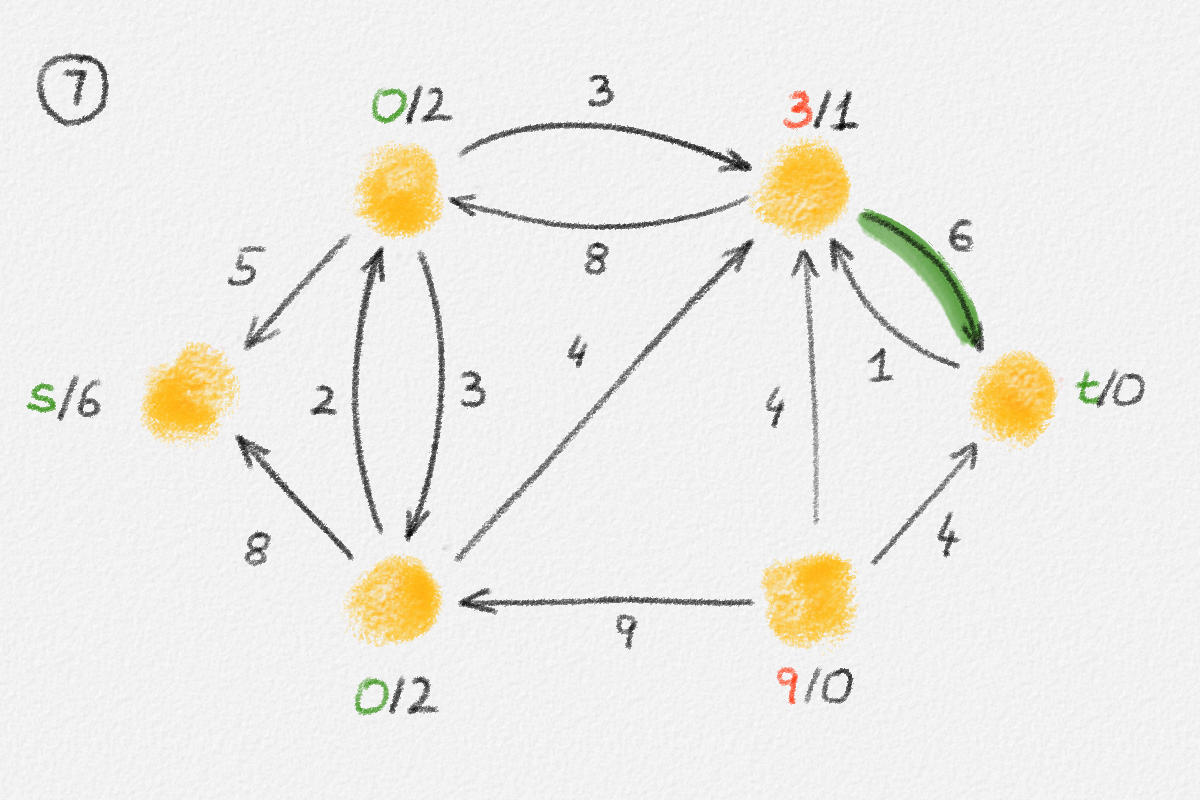
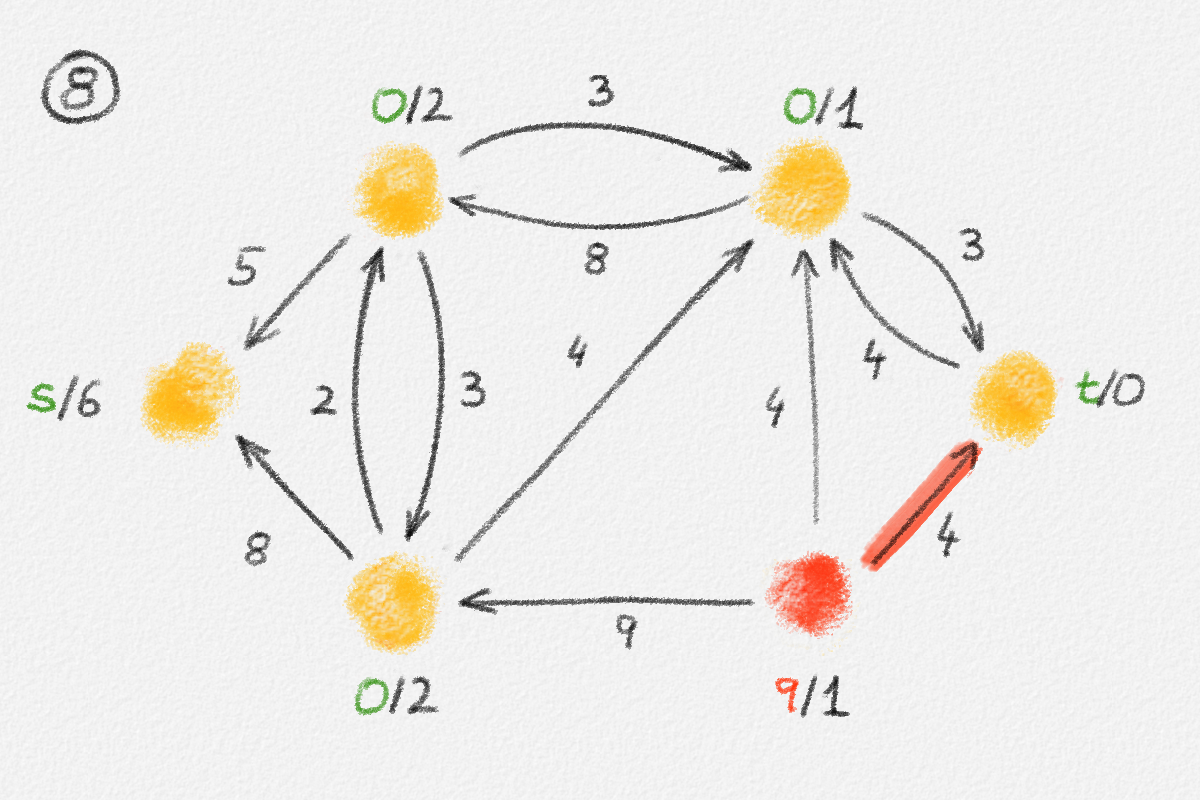
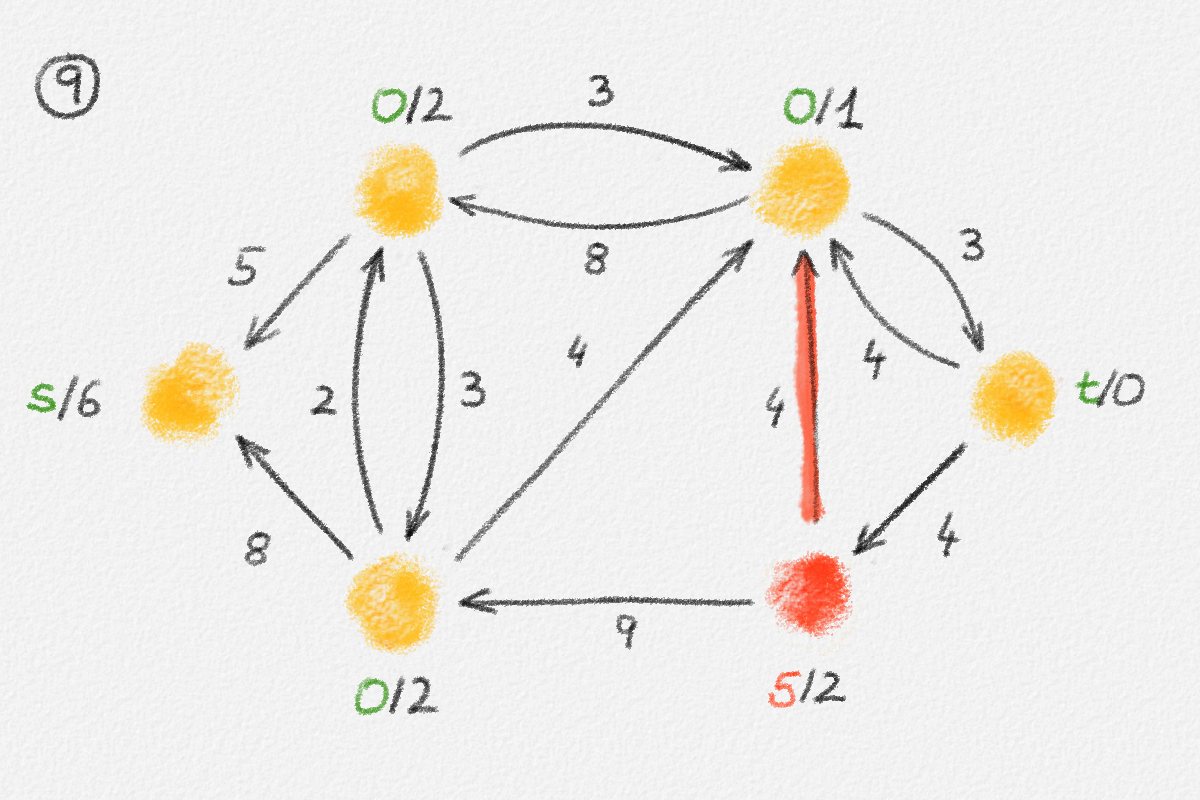
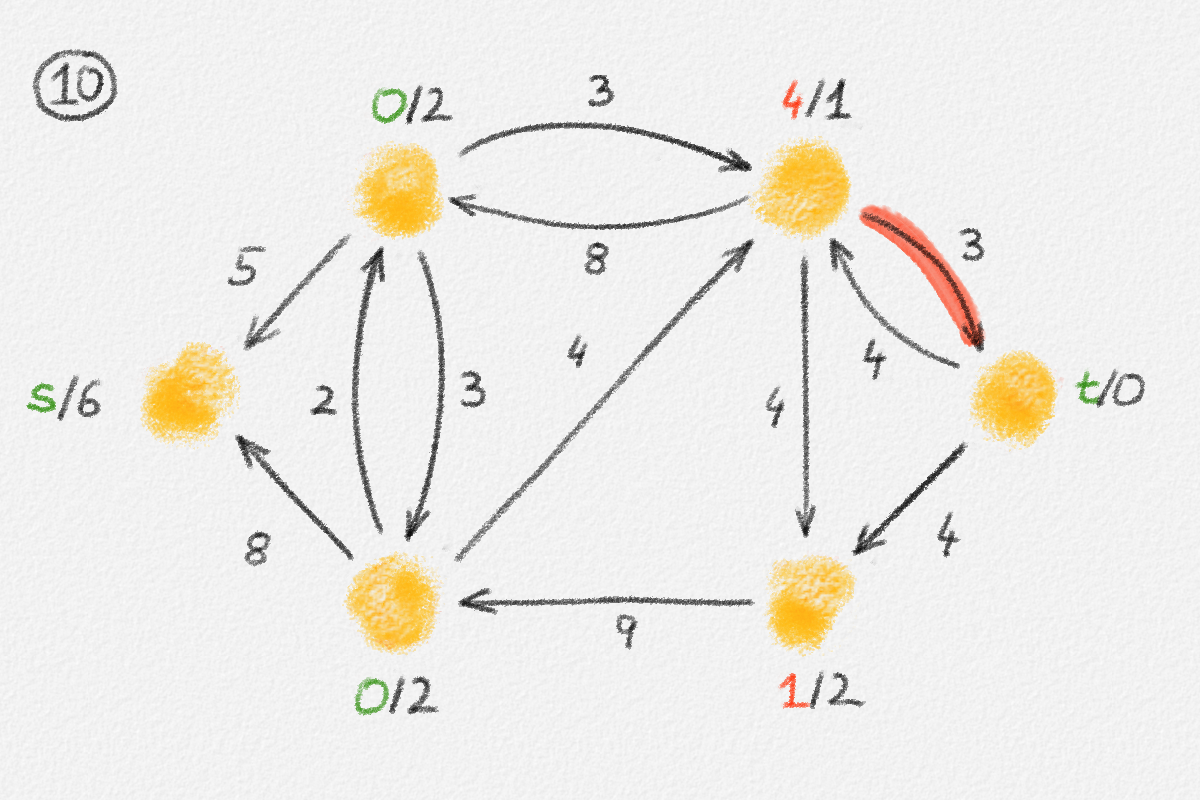
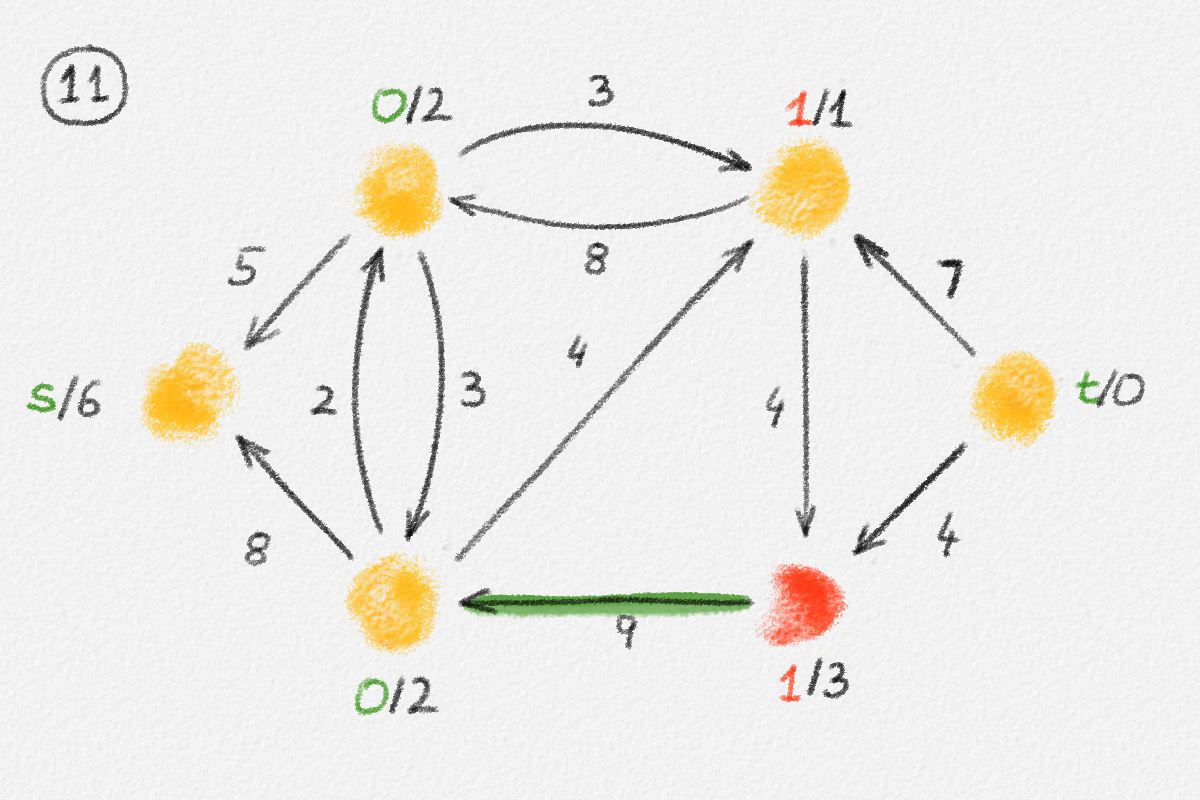
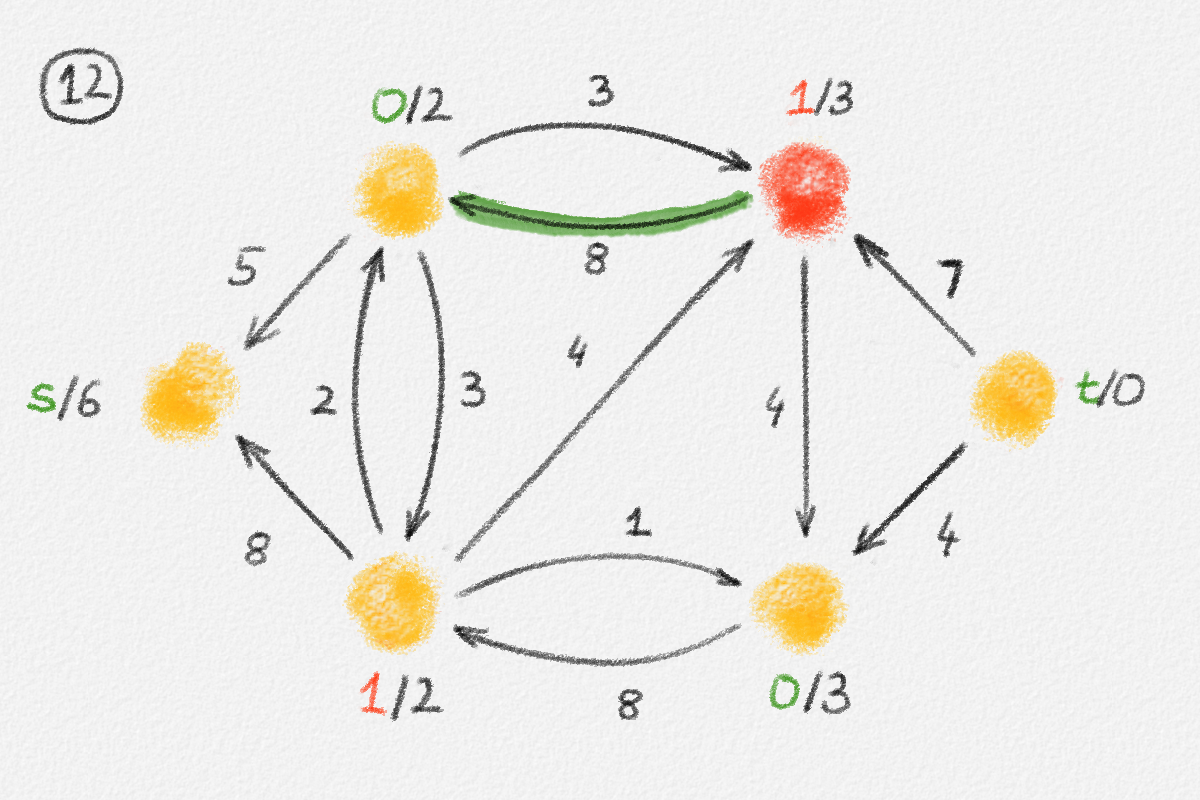
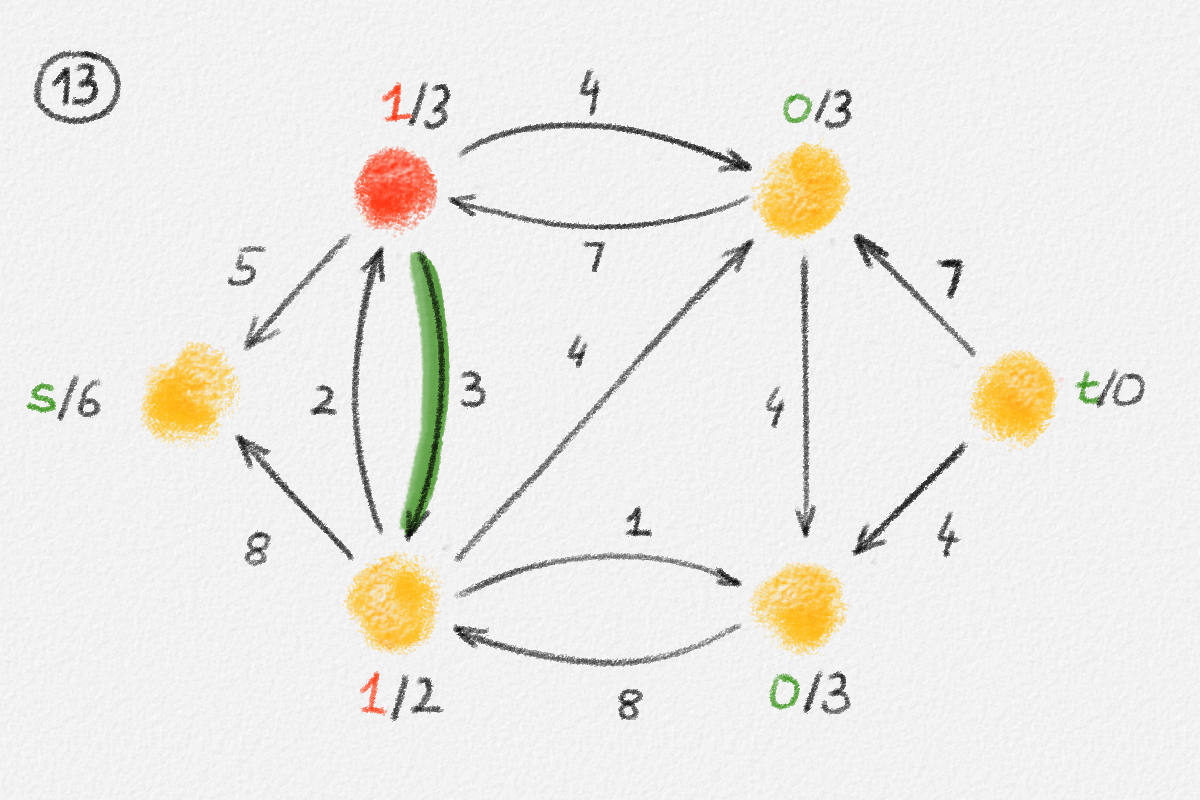
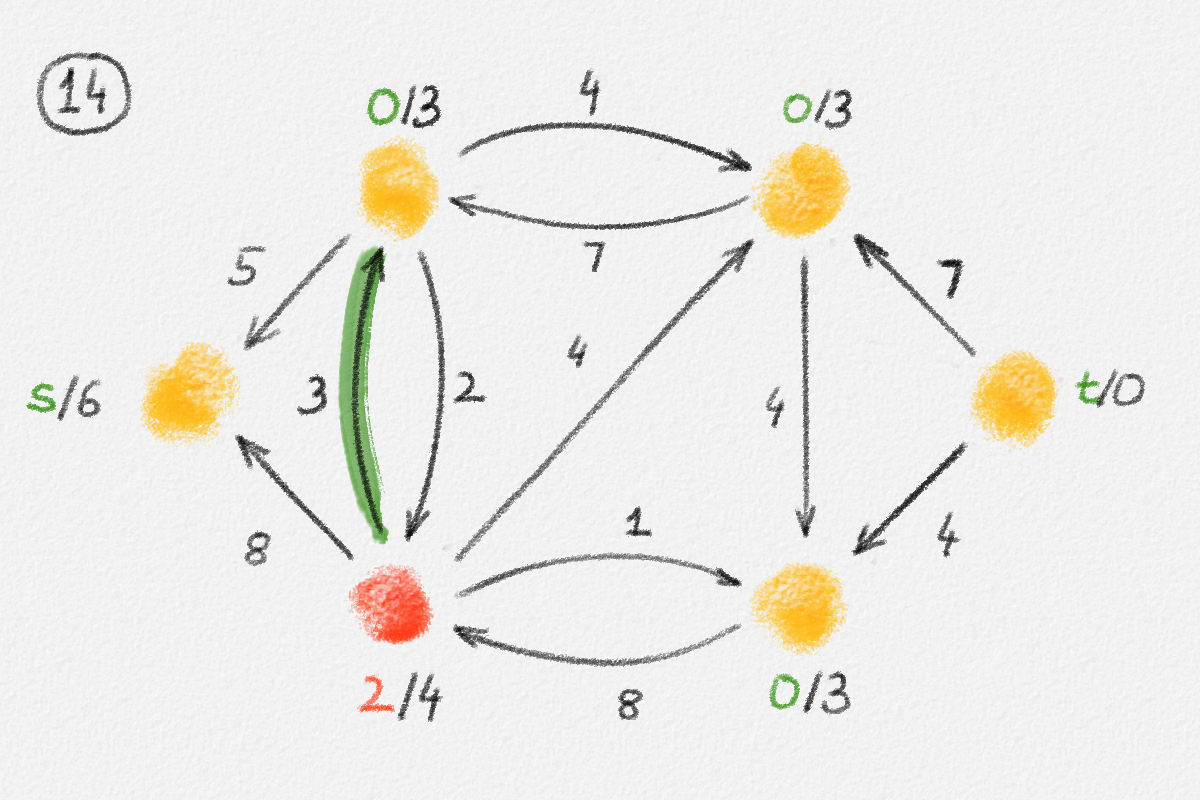
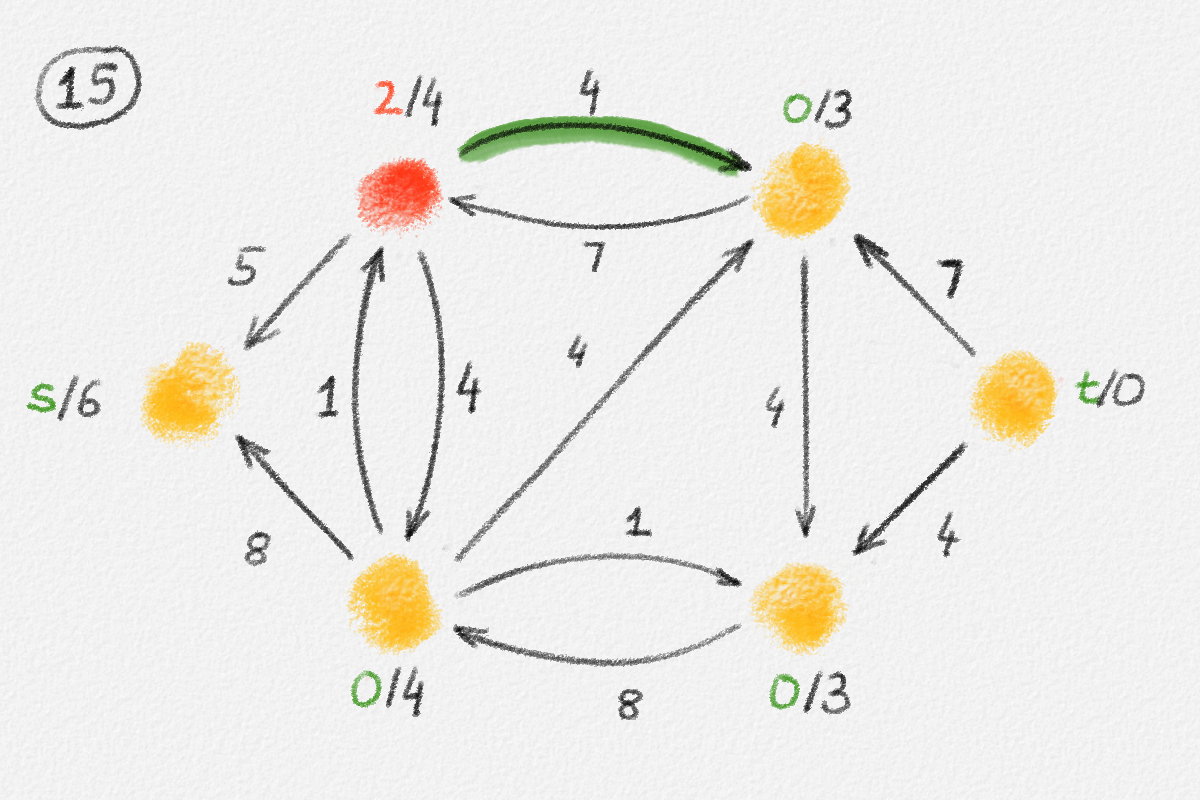
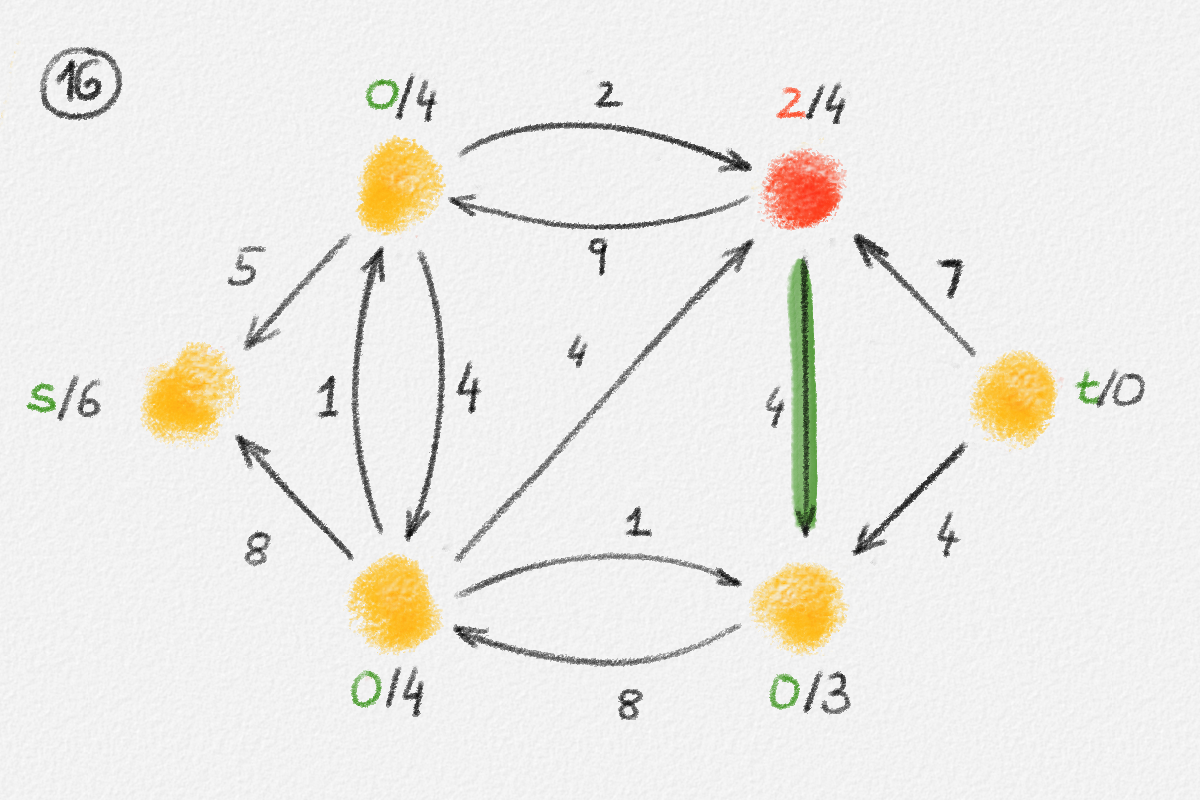
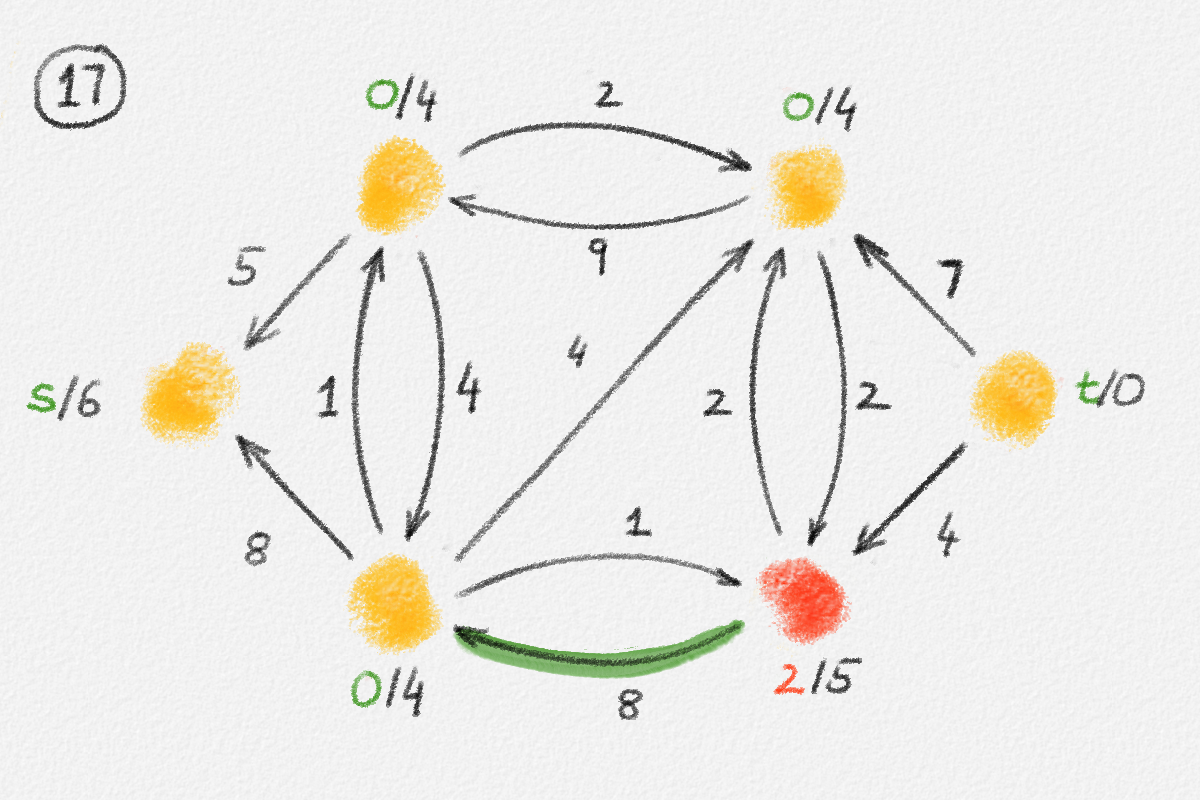
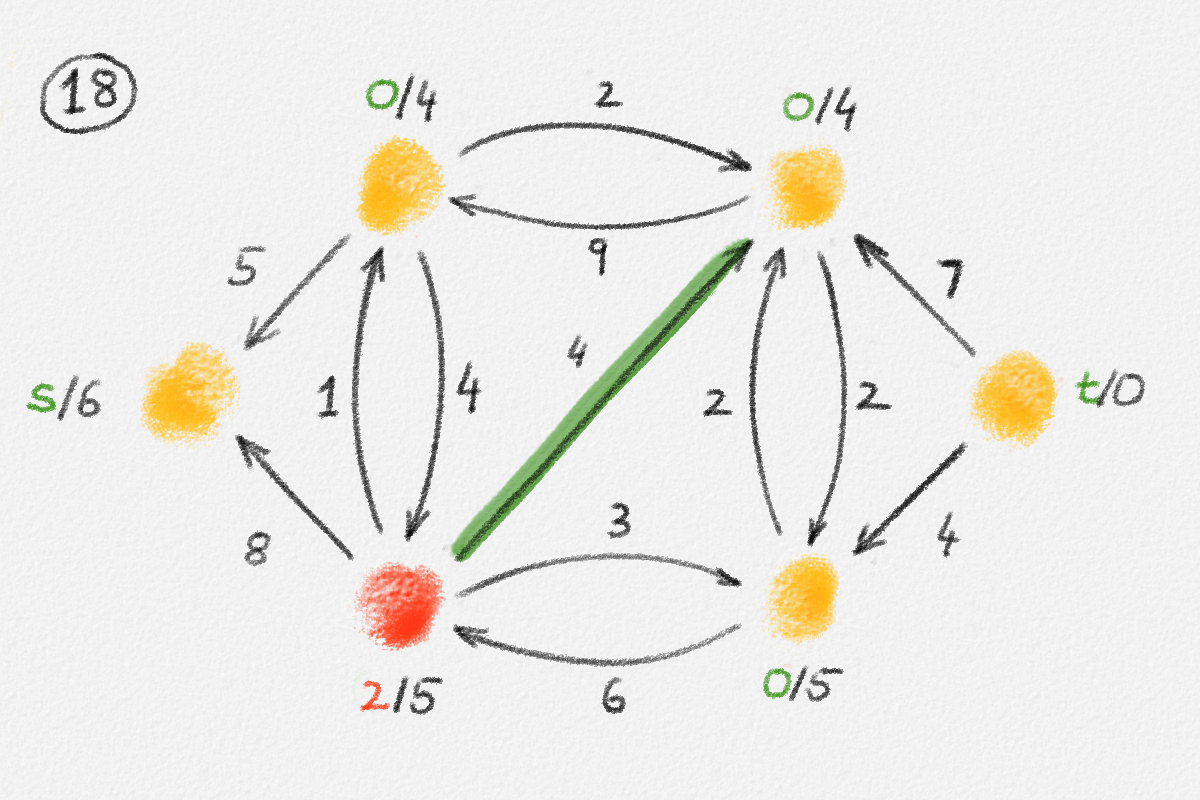
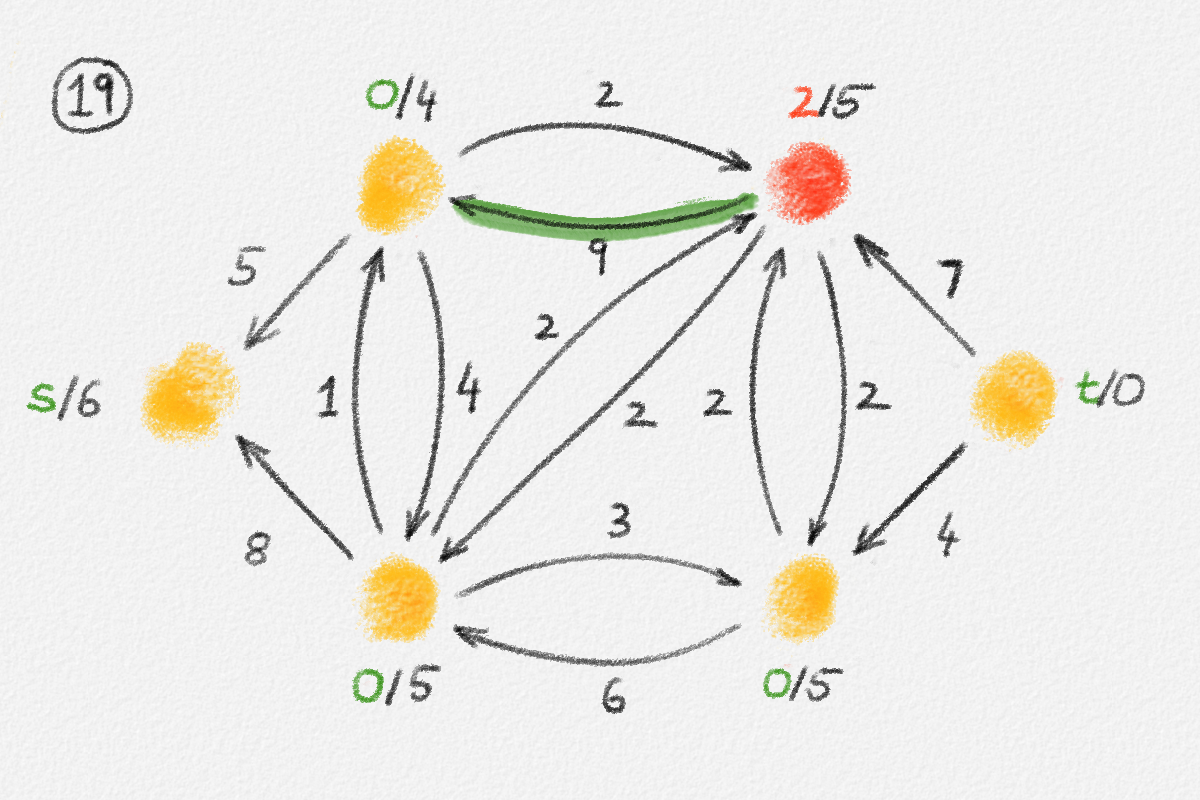
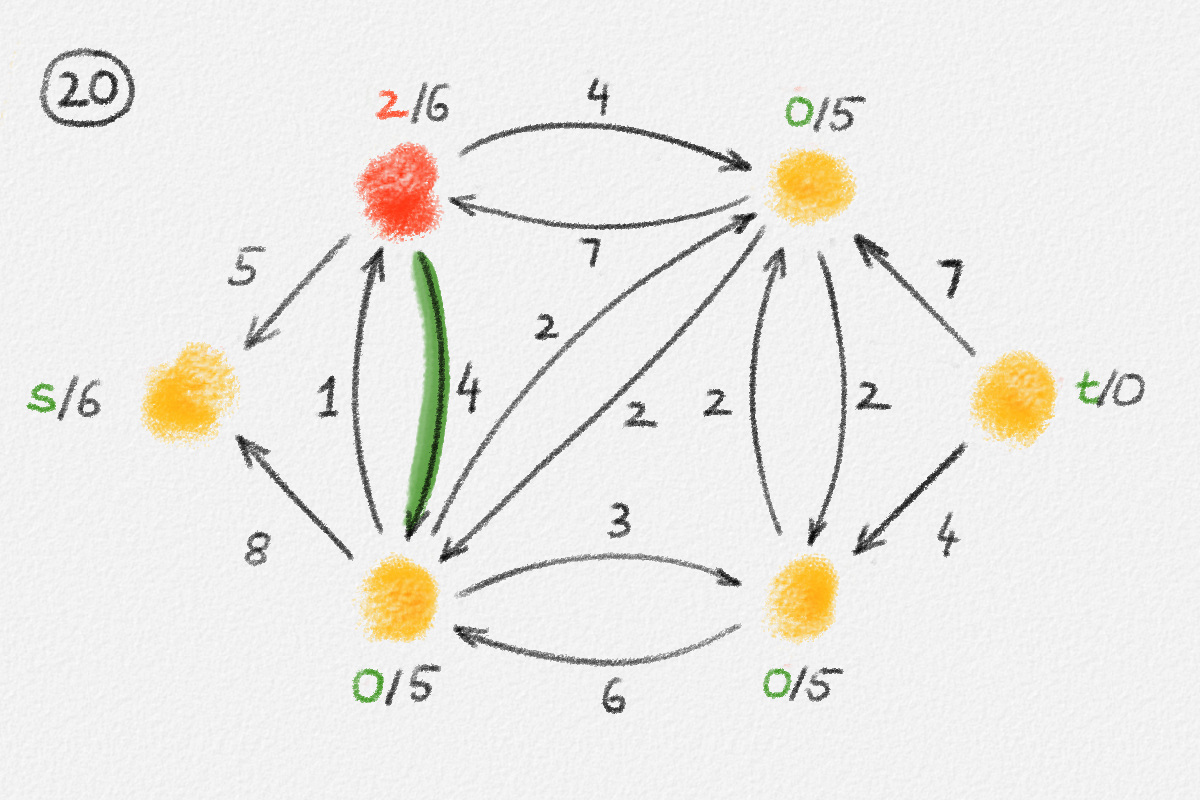
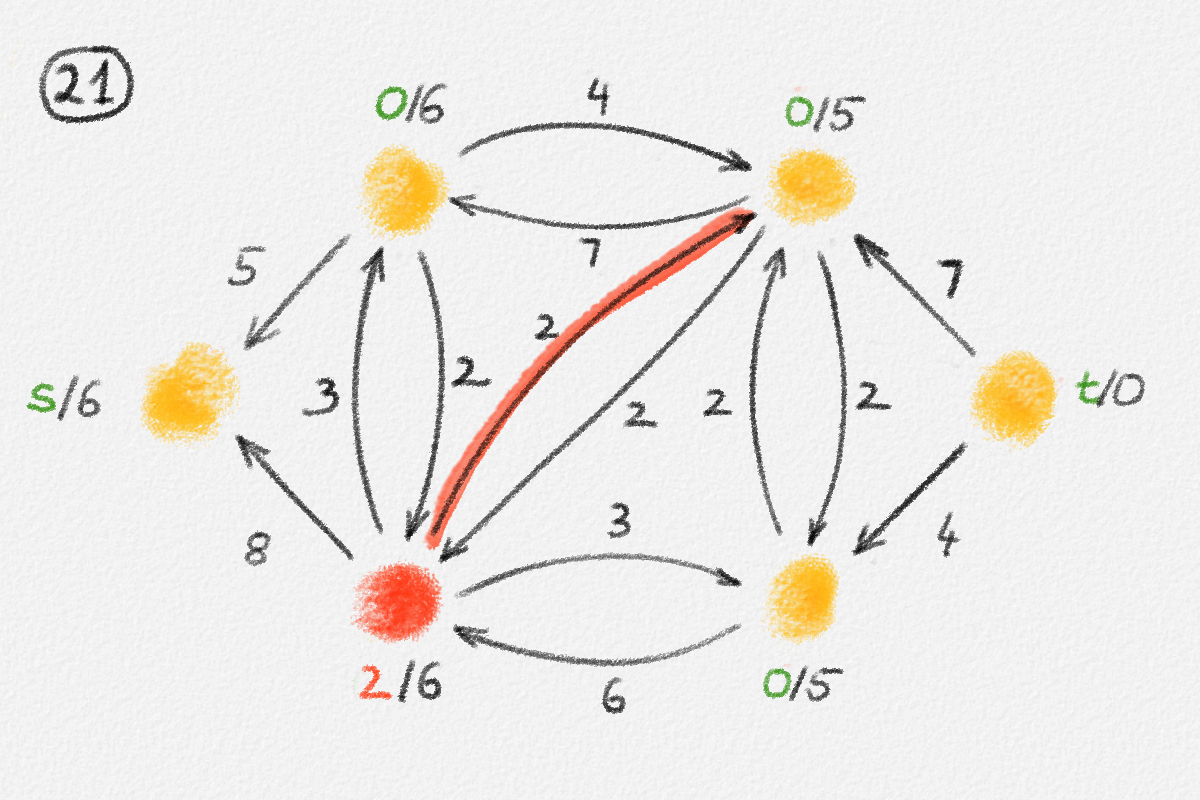
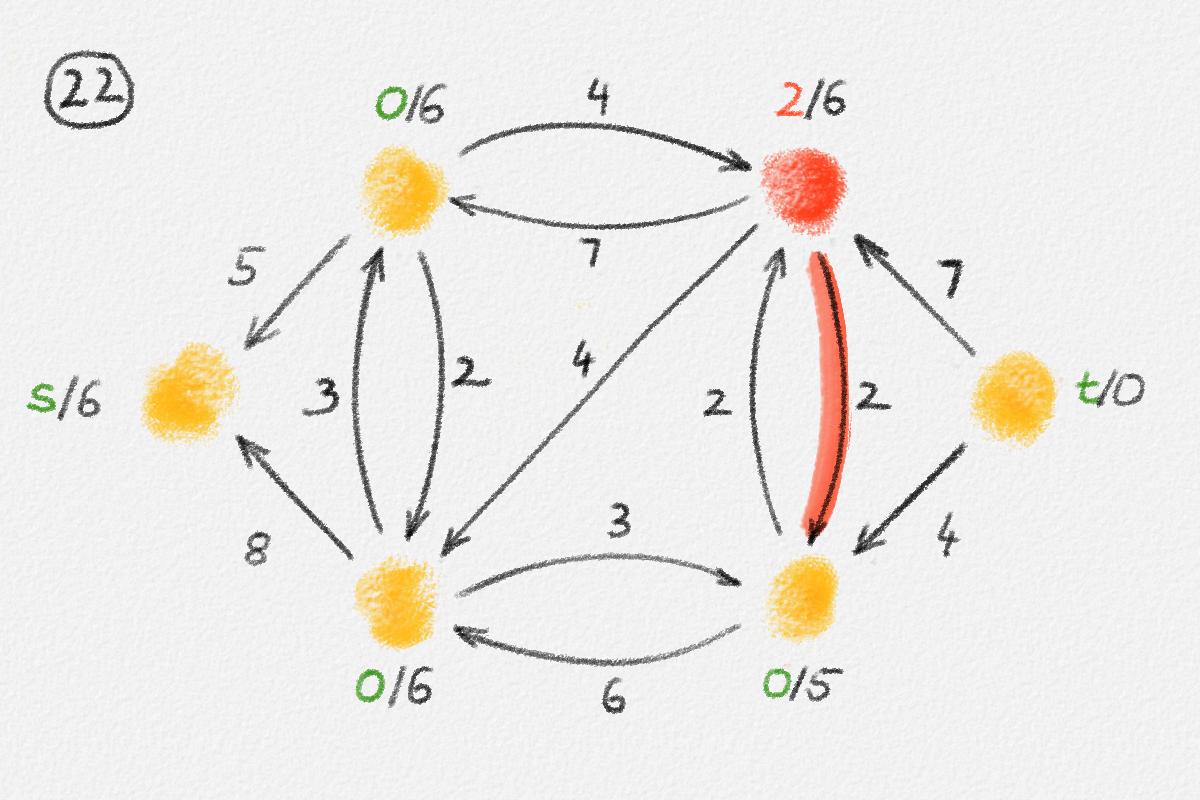
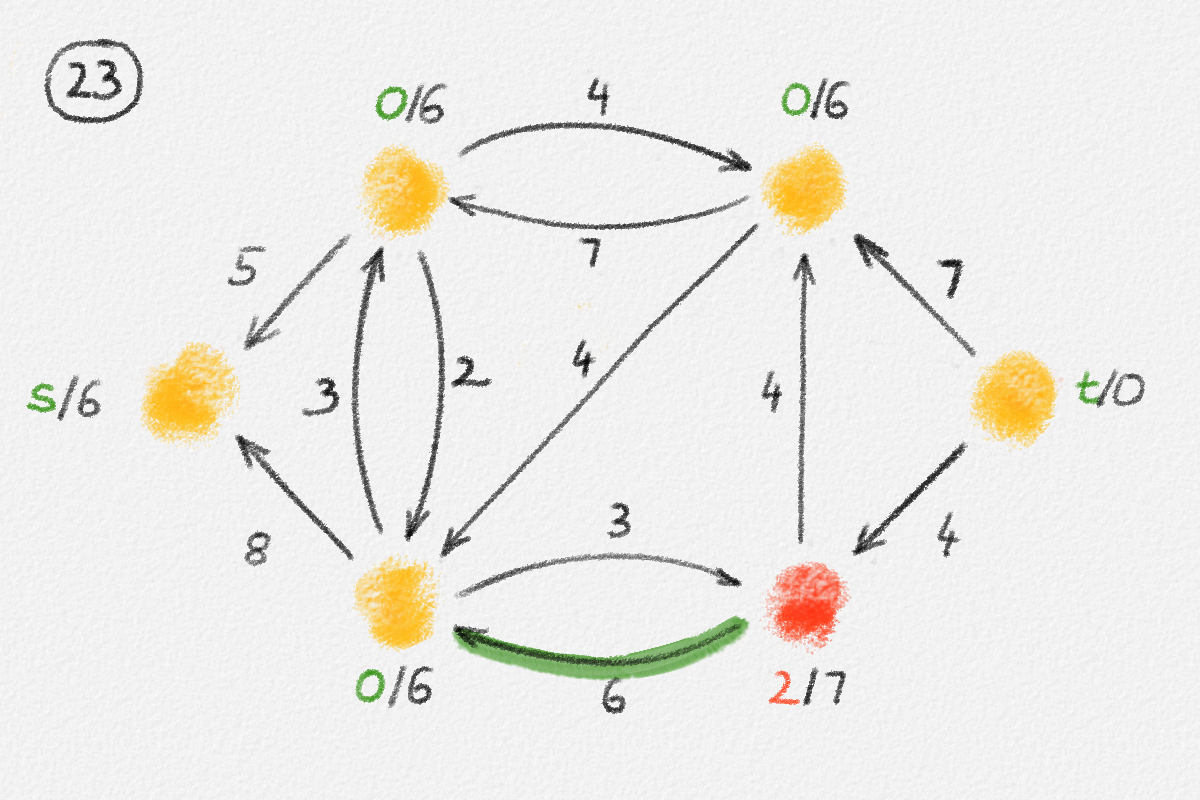
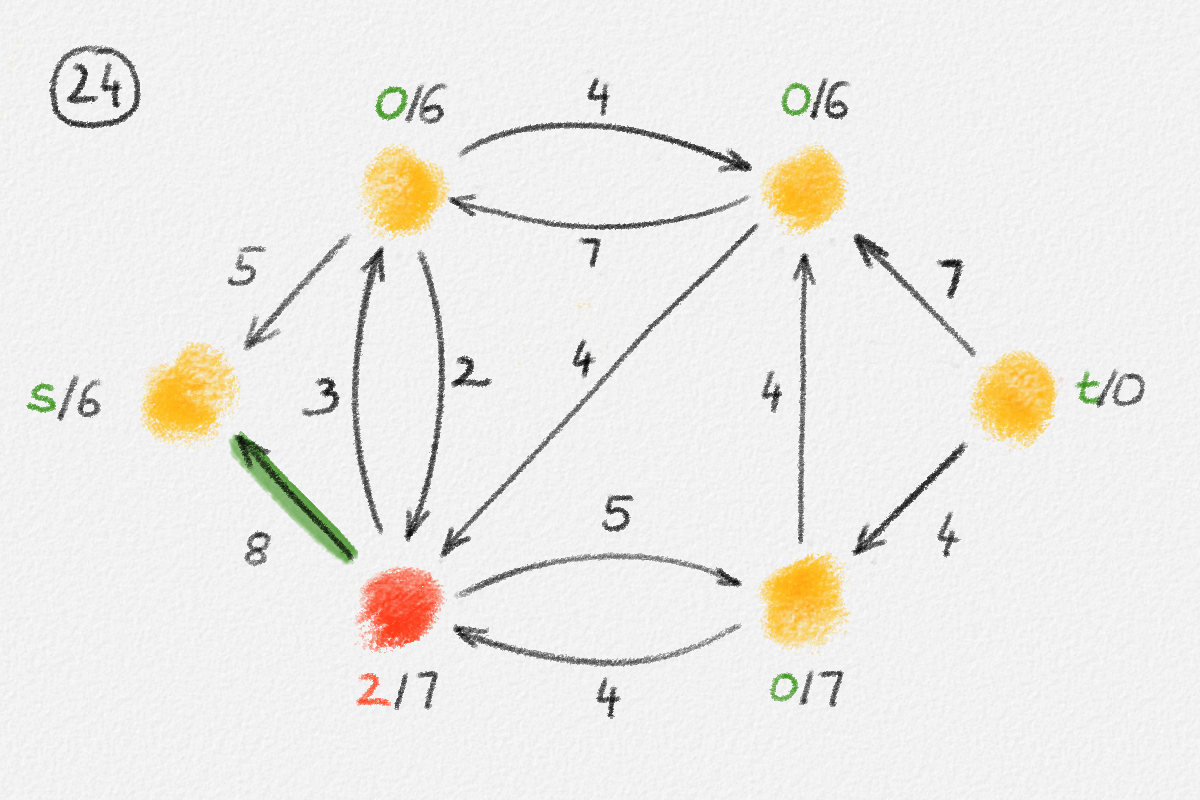
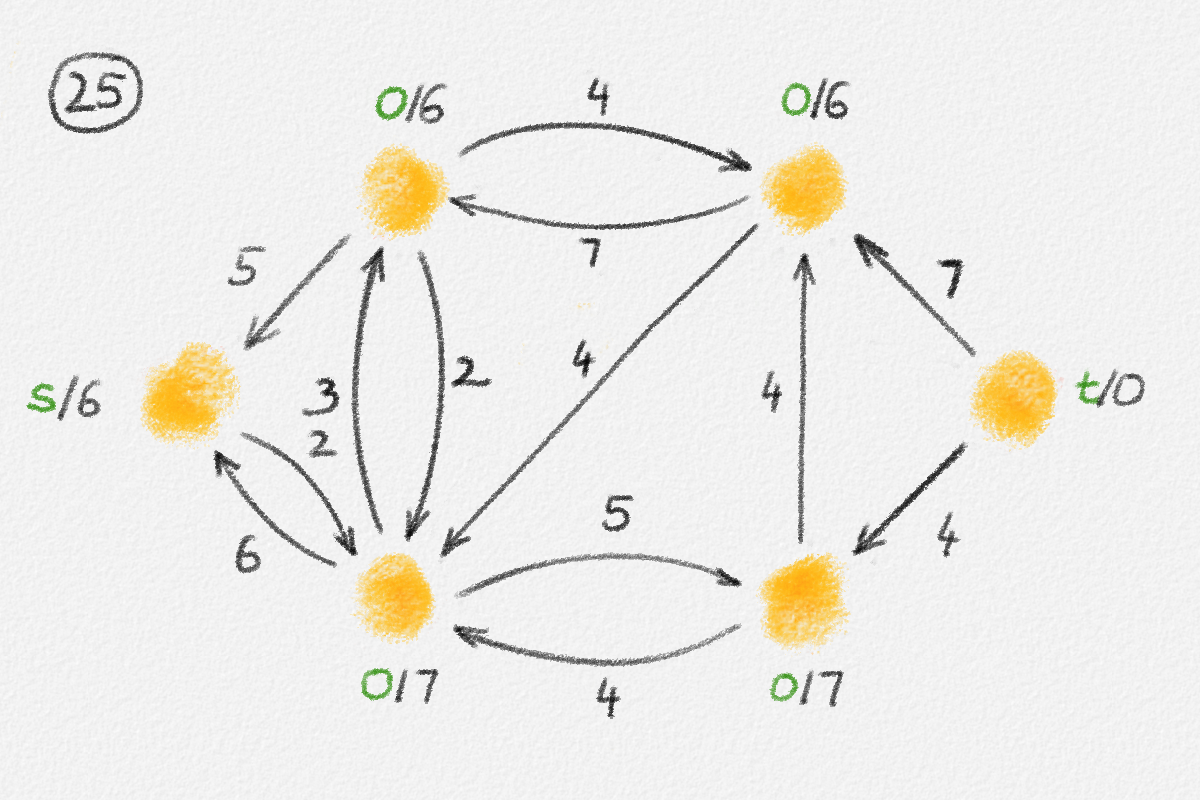
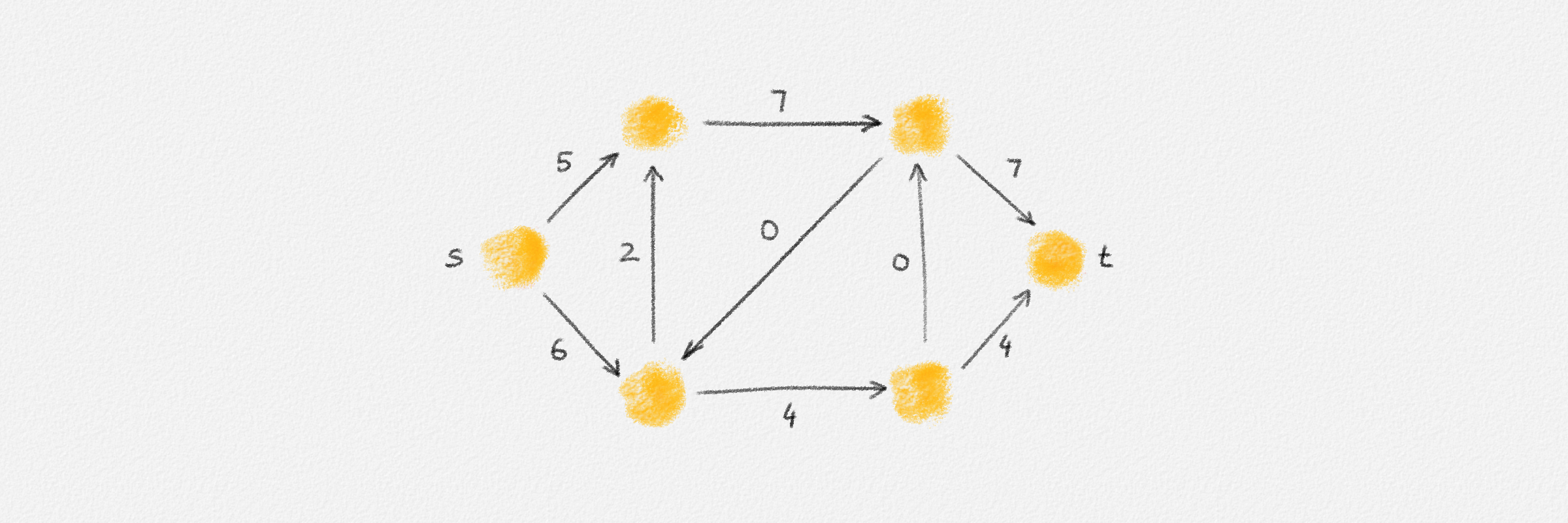
Figure 5.16: Illustration of an application of the generic preflow-push algorithm to the network in Figure 5.1. The circled numbers indicate the iteration number. Only the residual network is shown. Edge labels are edge capacities. Black node labels are node heights. Coloured node labels are node excesses, shown in red if positive and in green if zero. \(s\) and \(t\) are labelled with their names instead, to make them recognizable; they never overflow. In each figure, the edge used to push flow to a neighbour is shown in red if it is a saturating push or in green if it is a non-saturating push. If the tail of the edge was relabelled to allow this push to happen, this tail node is shown in red. The final network in the bottom row shows the computed flow.

Termination: If there is no vertex \(x \notin \{s, t\}\) with positive excess, then \(f\) is a feasible \(st\)-flow. Exit the algorithm and return \(f\). We prove below that \(f\) is not only a feasible \(st\)-flow but a maximum \(st\)-flow at this point.

Push: If there exist an overflowing vertex \(x \notin \{s, t\}\) and an edge \((x,y) \in G^f\) with \(h_y = h_x - 1\), then push

\[\delta = \min\Bigl(e_x, u^f_{x,y}\Bigr)\]

units of flow "downhill" from \(x\) to \(y\). Formally, set

\[\begin{aligned} f_{y,x} &= f_{y,x} - \min\bigl(\delta, f_{y,x}\bigr)\\ f_{x,y} &= f_{x,y} + \max\bigl(0, \delta - f_{y,x}\bigr)\\ e_x &= e_x - \delta\\ e_y &= e_y + \delta. \end{aligned}\]

Clearly, this does not decrease \(e_y\) and does not make \(e_x\) negative. Similar to the analysis of augmenting path algorithms, it also maintains the capacity constraint for the edge \((x,y)\). Thus, \(f\) remains a valid preflow. The operation also maintains the validity of the height function \(h\):

Observation 5.11: After a Push operation, \(h\) remains a valid height function.

Proof: A Push operation does not change \(h_z\) for any vertex \(z \in V\). Thus, the validity of \(h\) can only be affected by changes in the edge set of \(G^f\). Pushing flow from \(x\) to \(y\) can only make \((x,y)\) disappear from \(G^f\) and \((y,x)\) appear in \(G^f\). The former cannot invalidate \(h\). The latter does not invalidate \(h\) because \(h_x = h_y + 1\), so \(h_y \le h_x + 1\). ▨

A Push operation is called saturating if \(u^f_{x,y} = 0\) after the Push operation, that is, if \(f_{y,x} = 0\) and \(f_{x,y} = u_{x,y}\). Otherwise, it is non-saturating.

The only reason why a non-saturating Push operation chooses not to push more flow from \(x\) to \(y\), in an attempt to make it saturating, is because \(e_x < u^f_{x,y}\). This gives the following observation:

Observation 5.12: After a non-saturating Push operation along an edge \((x,y)\), \(e_x = 0\).

Relabel: If no overflowing vertex \(x \notin \{s, t\}\) has an out-edge \((x,y)\) in \(G^f\) that satisfies \(h_y = h_x - 1\), then pick an overflowing vertex \(x \notin \{s, t\}\) and set

\[h_x = 1 + \min \bigl\{ h_y \mid (x,y) \in G^f \bigr\}.\]

Note that this value is well defined because \(e_x > 0\) means that some amount of flow enters \(x\) through some in-edge \((y,x) \in E\) and thus the edge \((x,y)\) is in \(G^f\).

Observation 5.13: Relabelling \(x\) increases \(h_x\).

Proof: Since \(x\) is being relabelled, every out-neighbour \(y\) of \(x\) in \(G^f\) satisfies \(h_y \ge h_x\). Thus, setting \(h_x = 1 + \min \bigl\{ h_y \mid (x,y) \in G^f \bigr\}\) increases \(h_x\) by at least one. ▨

Observation 5.14: After relabelling \(x\), \(h\) remains a valid height function.

Proof: Increasing \(h_x\) can only lead out-edges \((x,y)\) of \(x\) in \(G^f\) to violate the condition that \(h_x \le h_y + 1\). Since a relabel operation sets \(h_x = 1 + \min \bigl\{ h_y \mid (x,y) \in G^f \bigr\}\), none of \(x\)'s out-edges violates this condition. ▨

The following lemma states that, as long as \(f\) is not a feasible \(st\)-flow, either a Push or a Relabel operation is applicable. Thus, the behaviour of the algorithm is well defined.

Lemma 5.15: As long as \(f\) is not a feasible \(st\)-flow, either a Push or a Relabel operation is applicable.

Proof: If \(f\) is not a feasible \(st\)-flow, then there exists an overflowing vertex \(x \notin \{s, t\}\). As observed above, \(x\) has at least one out-neighbour in \(G^f\). If one of these out-neighbours, \(y\), satisfies \(h_x = h_y + 1\), then we can push flow from \(x\) to \(y\). Otherwise, \(x\) can be relabelled. ▨

To summarize the preflow-push algorithm so far: We initialize \(f\) so that all out-edges of \(s\) are saturated while any other edge \((x, y)\) satisfies \(f_{x,y} = 0\). The height function \(h\) sets \(h_s = n\) and \(h_x = 0\) for all \(x \ne s\). Then we repeatedly pick a vertex \(x \notin \{s, t\}\) with positive excess \(e_x\) and we either move some of this excess to an out-neighbour \(y\) of \(x\) in \(G^f\) with \(h_y = h_x - 1\) (a Push operation) or we increase \(x\)'s height to one more than the minimum height of \(x\)'s out-neighbours in \(G^f\) (a Relabel operation). Note that after a Relabel operation, \(x\) is able to push some of its excess to at least one of its out-neighbours because at least one out-neighbour \(y\) satisfies \(h_y = h_x - 1\) now. We keep applying Push and Relabel operations until every vertex \(x \notin \{s, t\}\) has excess \(0\). At this point, \(f\) is a feasible \(st\)-flow, which the algorithm returns.

Next we prove that the preflow-push algorithm, if it terminates, returns a maximum \(st\)-flow.