7.4.1. Augmenting Paths

In this section, we introduce augmenting paths, the key concept needed in all matching algorithms for both bipartite and arbitrary graphs.

Given a matching \(M\) in a graph \(G\), bipartite or not, an alternating path is a path in \(G\) whose edges alternate between being in \(M\) and not being in \(M\). We call an alternating path even or odd if it is a path of even or odd length.

An alternating cycle is a cycle of even length whose edges alternate between being in \(M\) and not being in \(M\).

An augmenting path is an alternating path both of whose endpoints are unmatched.

In particular, an augmenting path must have odd length and must start and end with an unmatched edge. These definitions are illustrated in Figure 7.9.

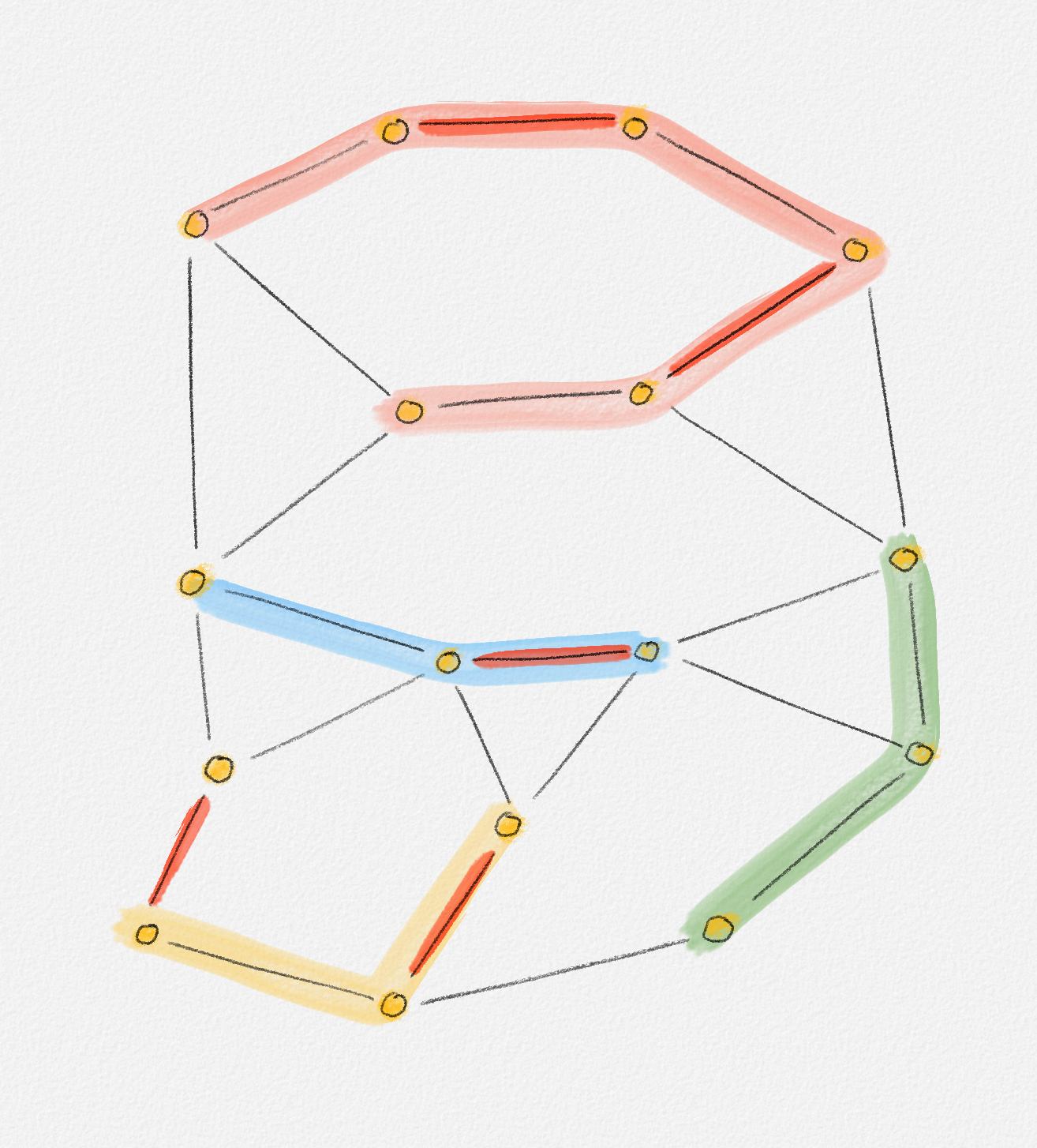
Figure 7.9: A graph \(G\) and a matching \(M\) (the red edges). The red, blue, and yellow shaded paths are alternating for \(M\). The red path is augmenting because its endpoints are both unmatched. The green path is not alternating because it contains two consecutive unmatched edges. For the red path \(R\) and the blue path \(B\), \(M \oplus R\) and \(M \oplus B\) are matchings. For the yellow path \(Y\), \(M \oplus Y\) is not a matching because its left endpoint is matched by an edge not in \(Y\).

For two edge sets \(E_1\) and \(E_2\), let \(E_1 \oplus E_2 = (E_1 \setminus E_2) \cup (E_2 \setminus E_1)\). The following lemma and its corollary give a useful characterization of maximum-cardinality matchings. See Figure 7.10 for an illustration.

Lemma 7.8: For two matchings \(M_1\) and \(M_2\), \(M_1 \oplus M_2\) is a collection of paths \(P_1, \ldots, P_k\) and cycles \(C_1, \ldots, C_\ell\). If \(a_1\) is the number of augmenting paths for \(M_1\) among \(P_1, \ldots, P_k\) and \(a_2\) is the number of augmenting paths for \(M_2\) among \(P_1, \ldots, P_k\), then \(|M_1| = |M_2| - a_1 + a_2\).

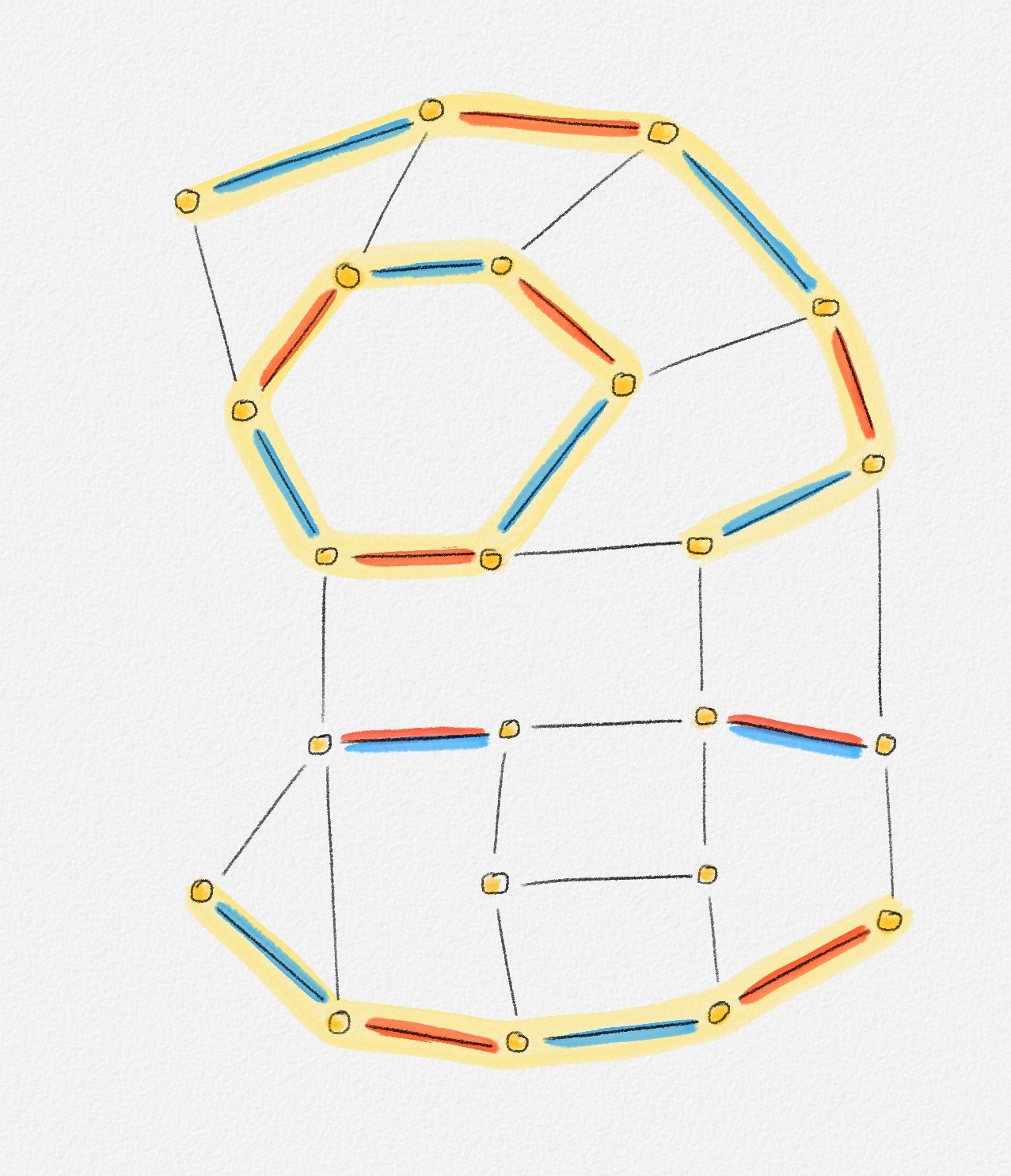
Figure 7.10: The symmetric difference \(M_1 \oplus M_2\) (shaded yellow) of two matchings \(M_1\) (red edges) and \(M_2\) (blue edges) is composed of a collection of alternating paths and cycles. In this example, one of the paths is an augmenting path for \(M_1\) and there are no augmenting paths for \(M_2\). Thus, \(|M_2| = |M_1| + 1\).

Proof: Every vertex has at most one incident edge in \(M_1\) and at most one incident edge in \(M_2\). Thus, it has at most two incident edges in \(M_1 \oplus M_2\). Since this is true for every vertex, \(M_1 \oplus M_2\) is a collection of paths and cycles.

We have \(|M_1| = |M_1 \cap M_2| + |M_1 \setminus M_2|\) and \(|M_2| = |M_1 \cap M_2| + |M_2 \setminus M_1|\). Thus,

\[\begin{aligned} |M_1| - |M_2| &= |M_1 \setminus M_2| - |M_2 \setminus M_1|\\ &= |M_1 \cap (M_1 \oplus M_2)| - |M_2 \cap (M_1 \oplus M_2)|\\ &= \sum_{i=1}^k\ \bigl(|M_1 \cap P_i| - |M_2 \cap P_i|\bigr) + \sum_{i=1}^\ell\ \bigl(|M_1 \cap C_i| - |M_2 \cap C_i|\bigr). \end{aligned}\]

Since \(M_1\) and \(M_2\) are matchings, the edges in every path \(P_i\) and every cycle \(C_i\) alternate between being in \(M_1\) and \(M_2\). Thus, every cycle \(C_i\) has even length and contains the same number of edges from \(M_1\) and \(M_2\), that is, \(|M_1 \cap C_i| - |M_2 \cap C_i| = 0\) for all \(1 \le i \le \ell\). Similarly, every even-length path \(P_i\) contains the same number of edges from \(M_1\) and \(M_2\), that is, \(|M_1 \cap P_i| - |M_2 \cap P_i| = 0\) for any such path.

Every odd-length path either contains one more edge from \(M_1\) than from \(M_2\) or one more edge from \(M_2\) than from \(M_1\). Let \(\mathcal{P}_1\) be the set of paths that contain one more edge from \(M_2\) than from \(M_1\), and let \(\mathcal{P}_2\) be the set of paths that contain one more edge from \(M_1\) than from \(M_2\). Then

\[|M_1| - |M_2| = |\mathcal{P}_2| - |\mathcal{P}_1|.\]

Next we prove that a path among \(P_1, \ldots, P_k\) belongs to \(\mathcal{P}_1\) if and only if it is an augmenting path for \(M_1\). By symmetry, a path among \(P_1, \ldots, P_k\) belongs to \(\mathcal{P}_2\) if and only if it is an augmenting path for \(M_2\). Thus, \(|\mathcal{P}_1| = a_1\), \(|\mathcal{P}_2| = a_2\), and \(|M_1| = |M_2| - a_1 + a_2\), as claimed.

So consider a path \(P_i\) in \(\mathcal{P}_1\). Since \(P_i\) is an alternating path with respect to \(M_1\), to prove that \(P_i\) is an augmenting path for \(M_1\), we need to prove that its endpoints \(x\) and \(y\) are unmatched by \(M_1\). Consider \(x\). The proof that \(y\) is unmatched is analogous. Since the edges in \(P_i\) alternate between \(M_1\) and \(M_2\), and \(P_i\) contains one more edge from \(M_2\) than from \(M_1\), the edge \(e\) in \(P_i\) incident to \(x\) is in \(M_2\) and, since it is in \(M_1 \oplus M_2\), not in \(M_1\). Thus, if \(x\) were matched by \(M_1\), then the edge \(f\) in \(M_1\) incident to \(x\) would have to be a different edge, \(f \ne e\). Since \(e \in M_2\) and \(M_2\) is a matching, we have \(f \notin M_2\), so \(f \in M_1 \oplus M_2\). This shows that \(x\) would have two incident edges in \(M_1 \oplus M_2\), but being the endpoint of \(P_i\), it has degree one in \(M_1 \oplus M_2\). This is a contradiction, so \(x\) must be unmatched.

Now consider a path \(P_i\) that is an augmenting path for \(M_1\). By the definition of an augmenting path, \(P_i\) is an alternating path with respect to \(M_1\) whose endpoints are unmatched by \(M_1\). Thus, the first and last edges of \(P_i\) do not belong to \(M_1\). This implies that \(P_i\) has one more edge from \(M_2\) than from \(M_1\), that is, \(P_i \in \mathcal{P}_1\). ▨

The following corollary provides the characterization of a maximum-cardinality matching that all matching algorithms in this chapter are based on:

Corollary 7.9: A matching \(M\) is a maximum-cardinality matching if and only if there is no augmenting path in \(G\) with respect to \(M\). For an augmenting path \(P\), \(M' = M \oplus P\) is a matching of cardinality \(|M'| = |M| + 1\).

Proof: First assume that there exists an augmenting path \(P\) with respect to \(M\) and let \(M' = M \oplus P\). Note that \(M'\) is a matching: If it is not, then there exists a vertex \(x\) with two incident edges \(e, f \in M'\). At most one of these edges is in \(M\) because \(M\) is a matching. The other, say \(e\), is therefore in \(P \setminus M\). Since \(P\) is an augmenting path, all edges incident to the endpoints of \(e\), other than \(e\) itself, are in \(E \setminus (M \cup P)\) or in \(M \cap P\). None of these edges is in \(M' = (M \setminus P) \cup (P \setminus M)\), so \(x\) cannot have a second edge in \(M'\), \(f\), incident to it.

Next observe that \(M \oplus M' = P\). Since \(P\) is an augmenting path for \(M\), Lemma 7.8 shows that \(|M'| = |M| + 1\), that is, \(M\) is not a maximum-cardinality matching and the second part of the corollary holds.

Conversely, if \(M\) is not a maximum-cardinality matching, then let \(M'\) be a maximum-cardinality matching. Since \(|M'| > |M|\), one of the paths in \(M \oplus M'\) must be an augmenting path for \(M\), by Lemma 7.8. Thus, the first part of the corollary holds. ▨