7.7. General Maximum-Cardinality Matching

The overall strategy of the bipartite maximum matching algorithm in Section 7.4 does not use that the graph is bipartite at all. Indeed, Corollary 7.9 states that a matching is a maximum-cardinality matching if and only if there is no augmenting path; there is no requirement that the graph should be bipartite. Thus, we can find a maximum-cardinality matching in any graph by starting with the empty matching or with a maximal matching and then repeatedly finding augmenting paths and augmenting the matching until no augmenting path exists.

Where bipartiteness is used in the bipartite maximum matching algorithm is in finding an augmenting path efficiently. In a bipartite graph \(G = (U, W, E)\), every augmenting path, having odd length, needs to start at an unmatched vertex in \(U\) and end at an unmatched vertex in \(W\). Alternating BFS from the unmatched vertices in \(U\) allowed us to find such a path in \(O(m)\) time (or to decide that there is no augmenting path and the matching is therefore maximum).

It turns out that finding an augmenting path in an arbitrary undirected graph is significantly harder. The fact that we cannot meaningfully divide the unmatched vertices into two subsets, those in \(U\) and those in \(W\), so that the augmenting path we need to find starts in one of those sets and ends in the other is only a minor nuisance. The more fundamental problem is that non-bipartite graphs can have odd cycles, cycles of odd length. By Exercise 7.2, bipartite graphs do not. Figure 7.17 shows an example where performing BFS or DFS to construct an alternating forest fails to find an augmenting path even though such a path exists. The problem is the highlighted odd cycle.

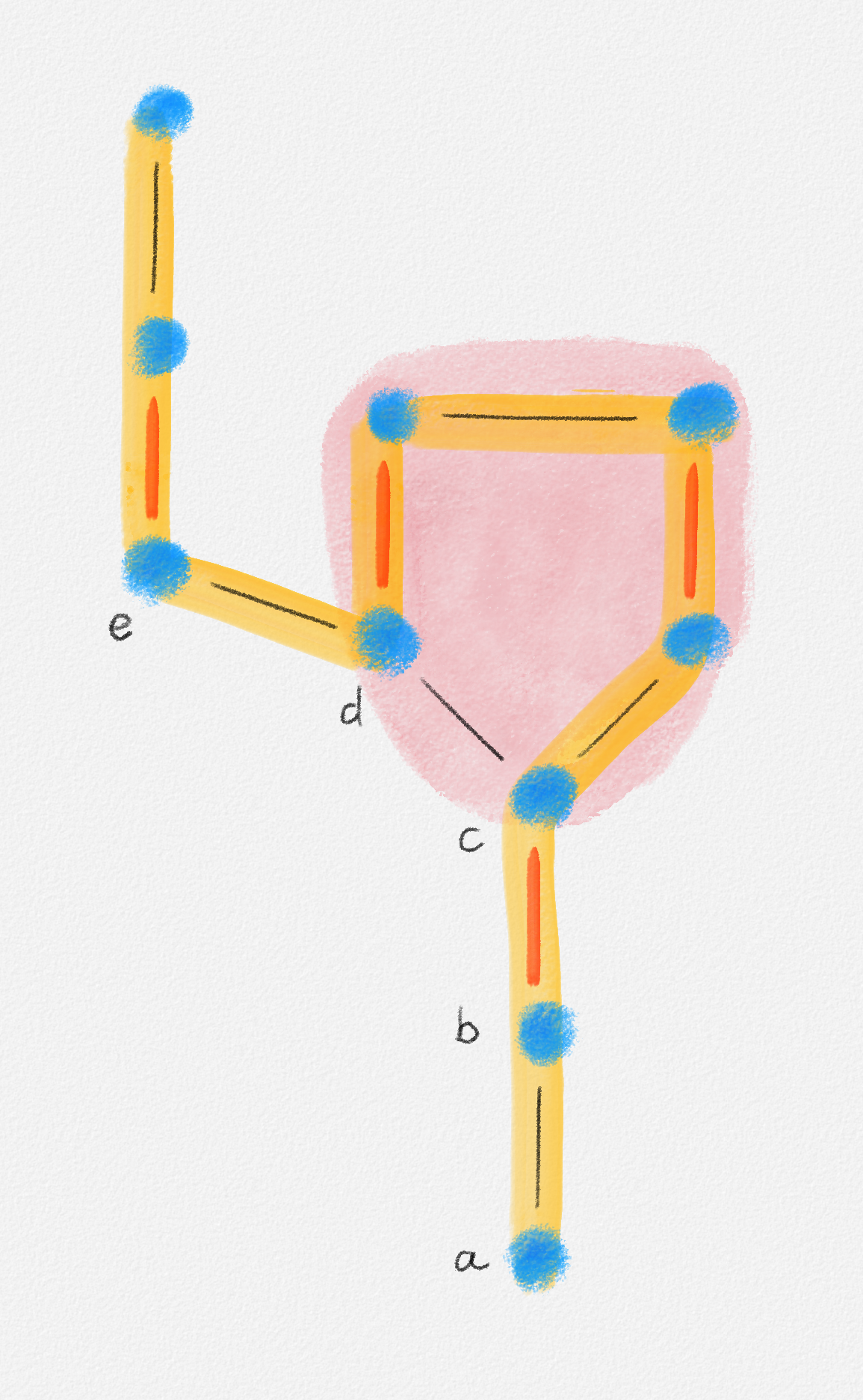
Figure 7.17: In this example, alternating BFS constructs an alternating forest that includes the path \(\langle a, b, c, d \rangle\). Alternating DFS may construct an alternating forest that includes this path. In any such forest, \(d\) is an odd vertex, so the edge \((d,e)\) is not included in the forest. In particular, the alternating forest does not include the yellow augmenting path. The problem in this example is the odd cycle shaded in pink. In order to discover the yellow augmenting path, we need to make our alternating forest travel around this cycle "in the right direction". This is what makes finding an augmenting path in non-bipartite graphs hard.

• In Section 7.7.1, we discuss Edmonds's algorithm for finding an augmenting path in an arbitrary graph in \(O(nm)\) time. The key strategy of Edmonds's algorithm can be described as follows: It runs alternating BFS from all unmatched vertices. It may then be possible to identify an augmenting path composed of two paths in the constructed alternating forest and an edge that joins them. If the algorithm finds such a path, it returns it. If it does not, then there are two possibilities: Either there is no augmenting path or there must exist a particular type of odd cycle, called a "blossom", composed of a path in the alternating forest plus one edge not in the forest. The algorithm is able to distinguish between these two cases. If there is no augmenting path, then the current matching is maximum and the algorithm exits. If there exists a blossom, the algorithm replaces the entire blossom with a single vertex: It "contracts" the blossom. It then recursively calls itself on the resulting smaller graph. If it fails to find an augmenting path in this smaller graph, then there is no augmenting path in the original graph either. Otherwise, an augmenting path in the original graph can be constructed easily from an augmenting path in the contracted graph. Since this strategy leads to an \(O(nm)\)-time algorithm to find an augmenting path and we can augment any matching at most \(\frac{n}{2}\) times before the matching is a maximum-cardinality matching, this leads to an \(O\bigl(n^2m\bigr)\)-time algorithm for finding a maximum-cardinality matching in an arbitrary graph.

• Just as we were able to reduce the time needed to find a maximum-cardinality matching in a bipartite graph from \(O(nm)\) to \(O\bigl(m\sqrt{n}\bigr)\), there have been numerous papers written on reducing the running time of Edmonds's algorithm to \(O(nm)\) and, by combining the ideas of Edmonds's algorithm with those of the Hopcroft-Karp algorithm for bipartite graphs, even to \(O\bigl(m\sqrt{n}\bigr)\). Even some of the current world-leading experts on matching algorithms find it difficult to fully verify the correctness of those algorithms. Thus, as at least a modest improvement over Edmonds's algorithm, we will discuss Gabow's implementation of Edmonds's algorithm in Section 7.7.2, which takes \(O\bigl(n^3\bigr)\) time. By implementing Gabow's algorithm using clever data structures, its running time can be reduced to \(O(nm \cdot \alpha(n))\), where \(\alpha\) is the inverse of Ackermann's function, a function that is never greater than a very small constant even for astronomical inputs. We will not discuss this faster implementation here.