2.3.2. Two Natural ILP Formulations of the MST Problem

The LP formulation of the SSSP problem is a fairly direct translation of the combinatorial formulation of the problem. When it comes to comparing greedy algorithms for the SSSP and MST problems, Kruskal's or Prim's algorithm seems to be more straightforward than Dijkstra's algorithm, at least in terms of the correctness proof. It is thus somewhat surprising that obtaining an efficient solution for the MST problem based on linear programming is significantly harder than for the SSSP problem.

Let us make a seemingly innocent change: We restrict the variables in the LP to being integers. An LP with this restriction is called, quite naturally, an integer linear program.

An integer linear program (ILP) is a linear program with the added constraint that all variable values in a feasible solution must be integers.

Since the MST problem is to choose the right subset of edges in \(E\) to be included in the edge set \(E'\) of the MST, it is natural to represent the set \(E'\) as a set of variables \(\{x_e \mid e \in E\}\) such that \(x_e = 1\) if \(e \in E'\) and \(x_e = 0\) if \(e \notin E'\). The weight of the MST \(T = (V, E')\) is then

\[w(T) = \sum_{e \in E} w_e x_e.\]

This is the objective function to be minimized. The constraints of the ILP need to enforce that \(T\) is a tree, that is, that \(T\) is connected and acyclic. The following exercise will be helpful in constructing the right set of constraints:

Exercise 2.3: Prove that a graph \(G\) on \(n\) vertices is a tree if and only if it has \(n - 1\) edges and

• Has no cycle or
• Is connected.

Our first two ILP formulations of the MST problem both enforce the constraint that \(T\) has \(n - 1\) edges:

\[\sum_{e \in E} x_e = n - 1.\]

To enforce that \(T\) is a tree, we need to add constraints that ensure that \(T\) is acyclic or that \(T\) is connected.

Enforcing That \(\boldsymbol{T}\) is Acyclic

Since \(T\) is a subgraph of \(G\), the only cycles that \(T\) can contain are cycles in \(G\). Thus, to ensure that \(T\) is acyclic, we need to ensure that there is no cycle \(C\) in \(G\) such that \(T\) contains all edges in \(C\); at least one edge from each cycle must be excluded from \(T\). This is easy to express as a set of linear constraints:

\[\sum_{e \in C} x_e \le |C| - 1 \quad \forall \text{cycle $C$ in $G$}.\]

This gives our first ILP formulation of the MST problem:

\[\begin{gathered} \text{Minimize } \sum_{e \in E} w_e x_e\\ \begin{aligned} \text{s.t. } \sum_{e \in E} x_e &= n - 1\\ \sum_{e \in C} x_e &\le |C| - 1 && \forall \text{cycle $C$ in $G$}\\ x_e &\in \{0, 1\} && \forall e \in E. \end{aligned} \end{gathered}\tag{2.9}\]

Note that this is an integer linear program: each variable \(x_e\) is not only constrained to be between \(0\) and \(1\)—this would make the problem a linear program—but is additionally required to be an integer. Since \(0\) and \(1\) are the only integers between \(0\) and \(1\), we thus require that \(x_e \in \{0, 1\}\) for all \(e \in E\).

Enforcing That \(\boldsymbol{T}\) is Connected

Our second ILP formulation of the MST problem ensures that \(T\) is a tree by requiring that it has \(n - 1\) edges and is connected. How can we express that a graph is connected? To do so, we need the notion of a cut:

A cut in a graph \(G = (V, E)\) is a partition of \(V\) into two non-empty subsets \(S\) and \(V \setminus S\). See Figure 2.10.

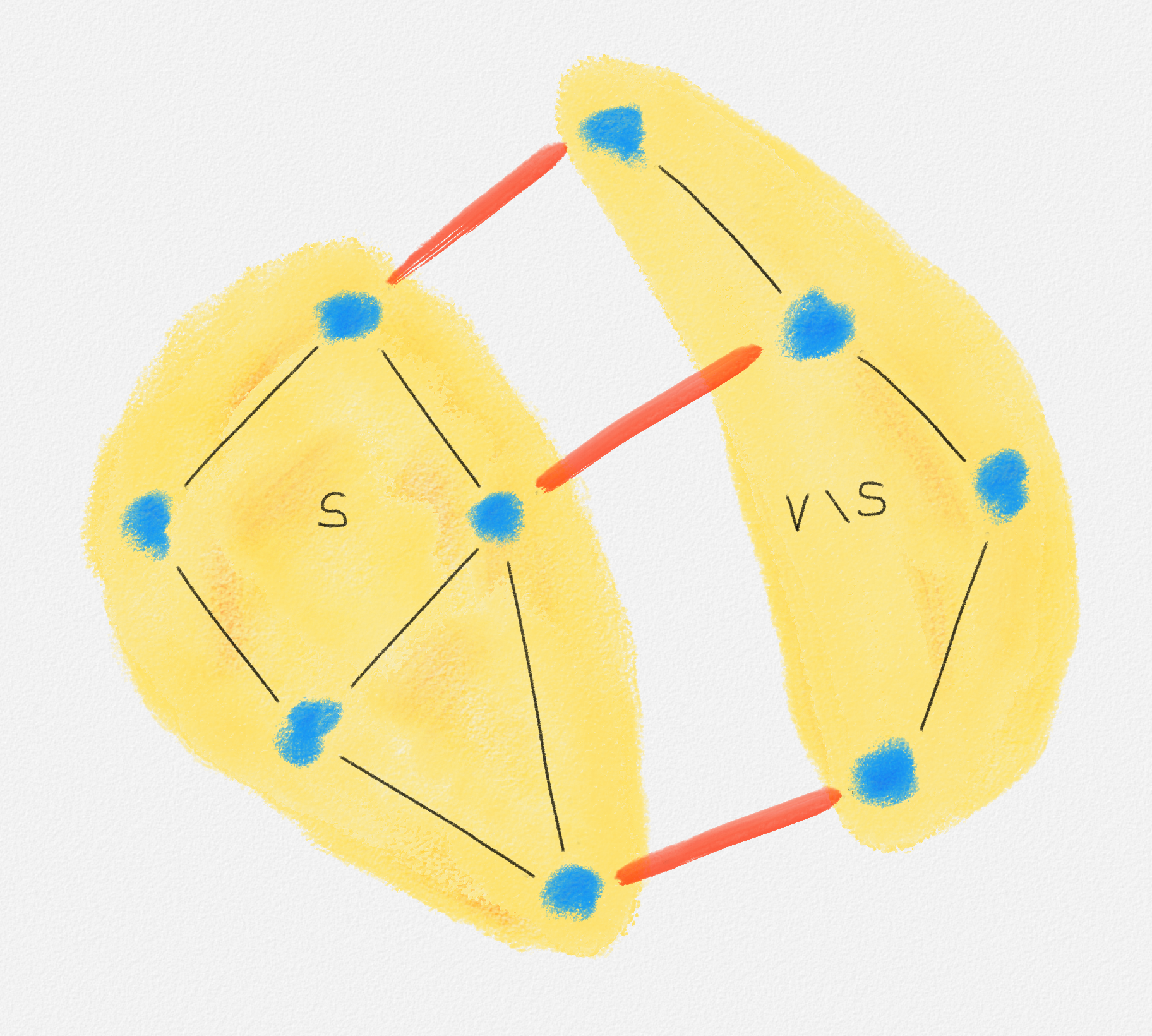
Figure 2.10: A cut \((S, V \setminus S)\). The red edges cross the cut.

Since the set \(V \setminus S\) is fixed once we specify \(S\), we will usually refer to any non-empty proper subset \(\emptyset \subset S \subset V\) as a cut. This ensures explicitly that \(S \ne \emptyset\), and the condition \(S \subset V\) ensures that \(V \setminus S \ne \emptyset\), so \((S, V \setminus S)\) is indeed the unique cut that has \(S\) as one of its halves.

An edge crosses the cut \(S\) if it has exactly one endpoint in \(S\). See Figure 2.10.

The following exercise shows how we can use cuts to express that a graph is connected.

Exercise 2.4: Prove that a graph \(G = (V,E)\) is connected if and only if every cut in \(G\) is crossed by at least one edge in \(E\).

Thus, our ILP formulation needs to ensure that the edge set \(E'\) of the tree \(T\) includes at least one edge that crosses each cut of \(G\):

\[\begin{gathered} \text{Minimize } \sum_{e \in E} w_e x_e\\ \begin{aligned} \text{s.t. } \sum_{e \in E} x_e &= n - 1\\ \sum_{e \text{ crosses } S} x_e &\ge 1 && \forall \text{cut $S$ in $G$}\\ x_e &\in \{0, 1\} && \forall e \in E. \end{aligned} \end{gathered}\tag{2.10}\]

From an algorithmic point of view, neither (2.9) nor (2.10) seems to be a very appealing formulation of the MST problem because they both involve a potentially exponential number of constraints: There can be an exponential number of cycles in \(G\) and there are \(2^{n-1} - 1\) cuts in an \(n\)-vertex graph. This suggests that solving either ILP should take exponential time. As we will see in Section 2.4, this is basically correct but not because the number of constraints is exponential but because integer linear programming is much harder than linear programming. So the "innocent change" to restrict variables to having integral values is far from innocent. In contrast, Prim's or Kruskal's algorithm can elegantly compute an MST in polynomial time.