2.5.1. ILPs With Integrality Gap 1

In some instances, the optimal solution of the LP relaxation of an ILP is integral, that is, every variable has an integer value. By Lemma 2.8, this implies that the optimal solution of the LP relaxation is also an optimal solution of the ILP.

In the remainder of this section, we explore whether the MST problem is such a problem. The answer depends on the chosen ILP formulation. For each of (2.9), (2.10), and (2.11), there exists an input that has a fractional solution with a lower objective function value than the best possible integral solution, as shown in the following three examples.

The "No Cycles" Formulation

As already observed, the LP relaxation of (2.9) is

\[\begin{gathered} \text{Minimize } \sum_{e \in E} w_e x_e\\ \begin{aligned} \text{s.t. } \sum_{e \in E} x_e &= n - 1\\ \sum_{e \in C} x_e &\le |C| - 1 && \forall \text{cycle $C$ in $G$}\\ 0 &\le x_e \le 1 && \forall e \in E. \end{aligned} \end{gathered}\tag{2.13}\]

Any MST of the graph in Figure 2.14 has weight \(10\).

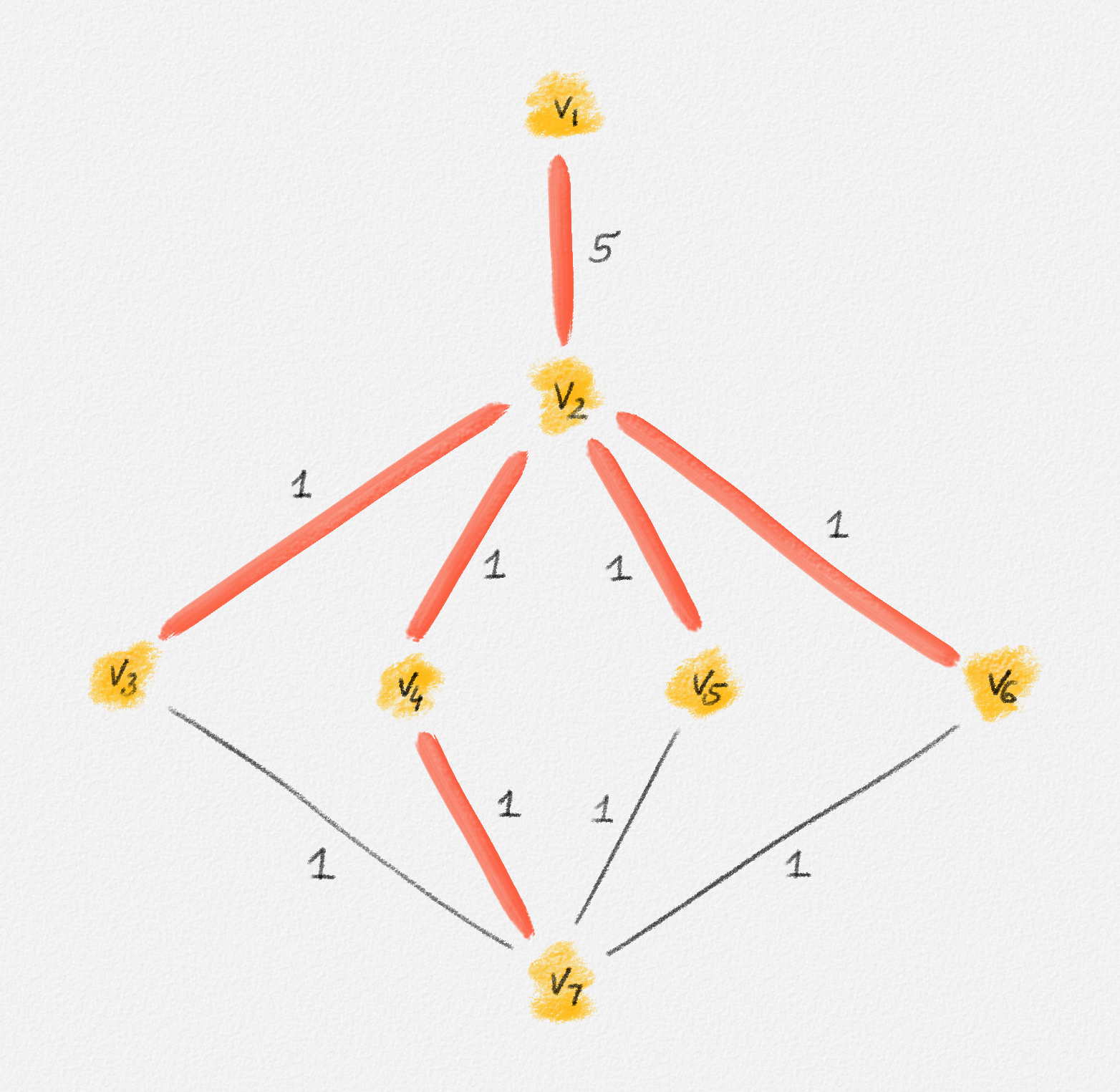
Figure 2.14: The edge labels are edge weights. The red tree has weight \(10\) and is an MST.

On the other hand, the following fractional solution with objective function value \(6\) satisfies all constraints of (2.13):¹

\[\begin{aligned} x_{12} &= 0\\ x_{23} = x_{24} = x_{25} = x_{26} &= \frac{1}{2}\\ x_{37} = x_{47} = x_{57} = x_{67} &= 1 \end{aligned}\]

The "Connectivity" Formulation

The LP relaxation of (2.10) is

\[\begin{gathered} \text{Minimize } \sum_{e \in E} w_e x_e\\ \begin{aligned} \text{s.t. } \sum_{e \in E} x_e &= n - 1\\ \sum_{e \text{ crosses } S} x_e &\ge 1 && \forall \text{cut $S$ in $G$}\\ 0 &\le x_e \le 1 && \forall e \in E. \end{aligned} \end{gathered}\tag{2.14}\]

Any MST of the graph in Figure 2.15 has weight \(2\).

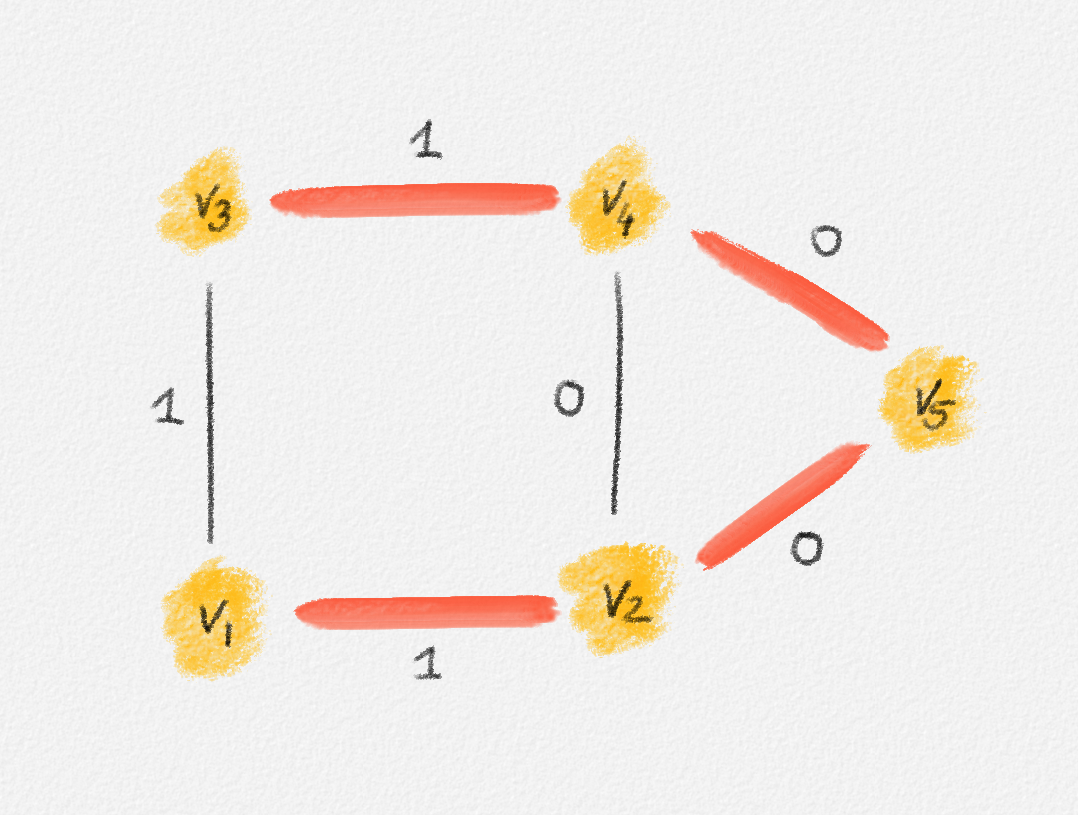
Figure 2.15: The edge labels are edge weights. The red tree has weight \(2\) and is an MST.

On the other hand, the following fractional solution with objective function value \(\frac{3}{2}\) satisfies all constraints of (2.12):

\[\begin{aligned} x_{12} = x_{13} = x_{24} = x_{34} &= \frac{1}{2}\\ x_{25} = x_{45} &= 1 \end{aligned}\]

The Polynomial-Size Formulation

The LP relaxation of (2.11) is

\[\begin{gathered} \text{Minimize } \sum_{e \in E} w_e x_e\\ \begin{aligned} \text{s.t. } \phantom{y_{(u,v)}^u + y_{(u,v)}^v} \llap{\displaystyle\sum_{e \in E} x_e} &= n - 1\\ y_{u,v}^u + y_{u,v}^v &= x_{u,v} && \forall (u,v) \in E\\ \sum_{(s,v) \in E} y_{s,v}^s &= 0\\ \sum_{(u,v) \in E} y_{u,v}^v &= 1 && \forall v \ne s\\ y_{u,v}^z &\ge y_{u,v}^v + y_{v,w}^z - 1\quad && \forall z \in V, (u,v) \in E, (v,w) \in E\\ 0 \le x_e &\le 1 && \forall e \in E\\ 0 \le y_e^v &\le 1 && \forall v \in V, e \in E. \end{aligned} \end{gathered}\tag{2.15}\]

Any MST of the graph in Figure 2.16 has weight \(10\).

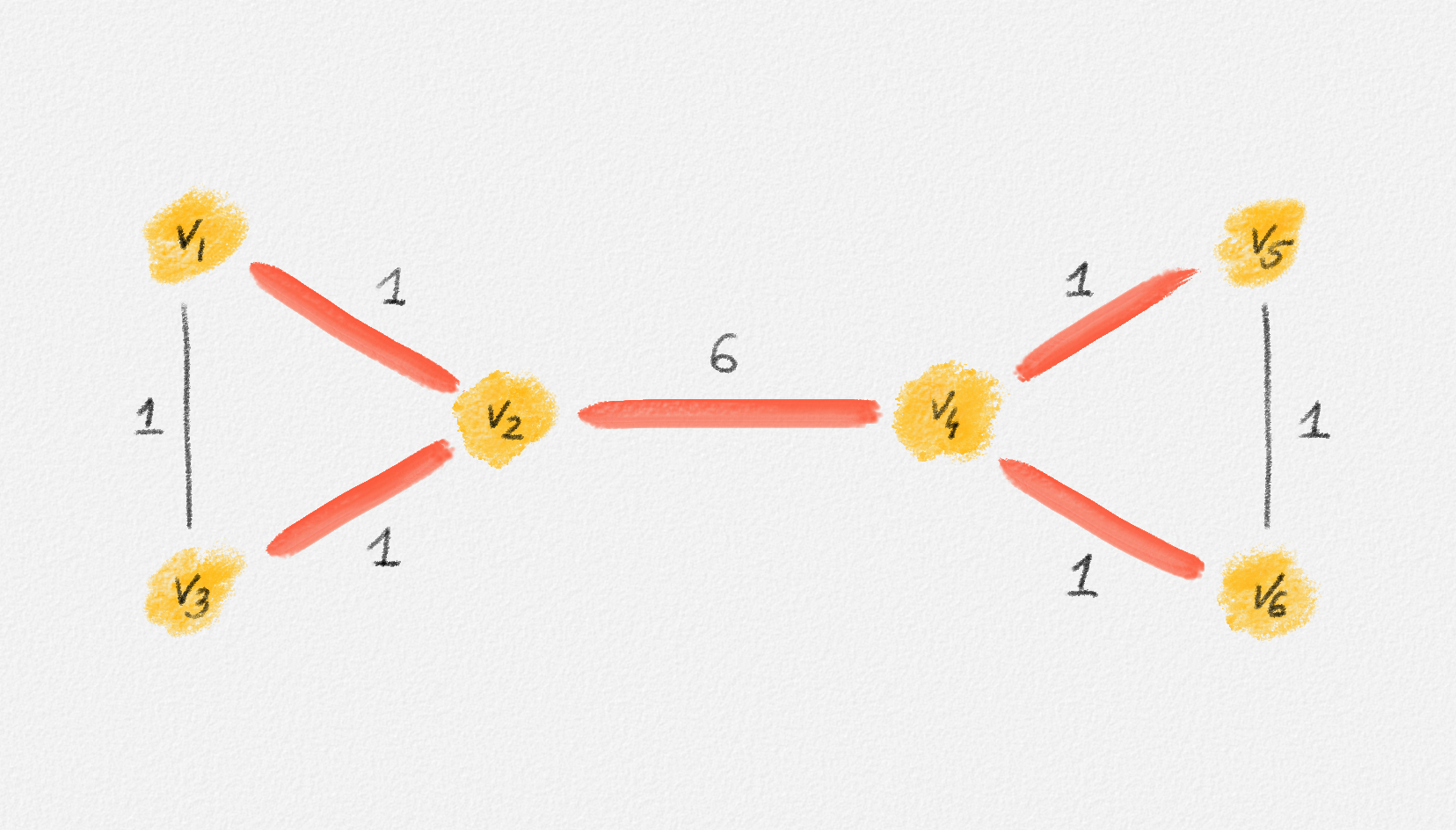
Figure 2.16: The edge labels are edge weights. The red tree has weight \(10\) and is an MST.

No matter whether \(s = v_1\) or \(s = v_2\) (any other choice is symmetric to one of these two choices), there exists a feasible solution of (2.15) whose objective function value is only \(5\):

\[\begin{aligned} \boldsymbol{s = v_1:} && x_{13} = x_{24} &= 0 & x_{12} &= x_{23} = x_{45} = x_{46} = x_{56} = 1\\ && y_{13}^k = y_{24}^k &= 0 \quad \forall 1 \le k \le 6 & y_{45}^k &= y_{46}^k = y_{56}^k = \frac{1}{2} \quad \forall 1 \le k \le 6\\ && y_{12}^k &= 0 \quad \forall k \notin \{2, 3\} & y_{12}^k &= 1 \quad \forall k \in \{2, 3\}\\ && y_{23}^k &= 0 \quad \forall k \ne 3 & y_{23}^3 &= 1 \end{aligned}\]

\[\begin{aligned} \boldsymbol{s = v_2:} && x_{13} = x_{24} &= 0 & x_{12} &= x_{23} = x_{45} = x_{46} = x_{56} = 1\\ && y_{13}^k = y_{24}^k &= 0\quad \forall 1 \le k \le 6 & y_{45}^k &= y_{46}^k = y_{56}^k = \frac{1}{2} \quad \forall 1 \le k \le 6\\ && y_{12}^k &= 0 \quad \forall k \ne 1 & y_{12}^1 &= 1\\ && y_{23}^k &= 0 \quad \forall k \ne 3 & y_{23}^3 &= 1 \end{aligned}\]

As these three examples show, integrality matters for all three MST ILPs (2.9), (2.10), and (2.11). Next, we discuss an extension of (2.9) whose LP relaxation has an optimal integral solution.