Lists: Non-Determinism

Remember non-deterministic finite automata (NFA) from CSCI 2115. The idea was that when in some state \(s\) and reading some character \(x\), such an automaton may transition to more than one state. Non-determinism meant that the NFA was allowed to choose between any of these possible successor states. We also said that an NFA accepts a string if and only if there exists a set of these choices that it can make so that after reading the string, it ends up in an accepting state.

This all became fairly hairy to wrap our head around and to reason about formally, so we quickly switched to an entirely deterministic view that captures the same idea. We defined the transition function of an NFA to map each state-character pair \((s,x)\) to a set of states. This is the set of states that the NFA could be in after reading \(x\) in state \(s\). We then used this to define the set of states that the NFA could be in after reading a given string. The NFA accepts the string if and only if this set contains an accepting state. We were able to use this idea to convert our NFA into a DFA that decides the same language. The basic ideas was to use sets to track all possible computation paths that the NFA could take for a given string.

In Haskell, we can use lists as a first approximation to represent sets of values.¹ A function that can return more than one possible result for a given input simply returns a list of all possible results. That's a deterministic approach to modelling non-deterministic computations, just as our translation of an NFA into a DFA. Our goal is to turn lists into a monad. This allows us to model non-deterministic computations as functions that return lists of values, and to build larger non-deterministic computations by composing smaller non-deterministic steps.

Let's figure out what function composition should look like. Remember, function composition is the functional equivalent of sequencing steps. The function g . f applies f, then g. You can view this as sequencing, as running g after f. Our composition operator for decorated functions is (>=>). Let's think about sequencing two non-deterministic functions f and g. Their composition f >=> g should run f on its input, and then run g on whatever result f produces. Given that f and g are non-deterministic, f >=> g is also non-deterministic, that is, it may return one of many results on the same input. The way we represent this is that f >=> g returns a list of values. This list should contain all the values that could be produced by f >=> g. What are they?

f produces a list of values. Each of them is a value that f, viewed as a non-deterministic function, might return. Thus, we may apply g to any of these values. For each of these values x, g x produces the list of all values that it might return when viewed as a non-deterministic function. This is visualized in the following figure:

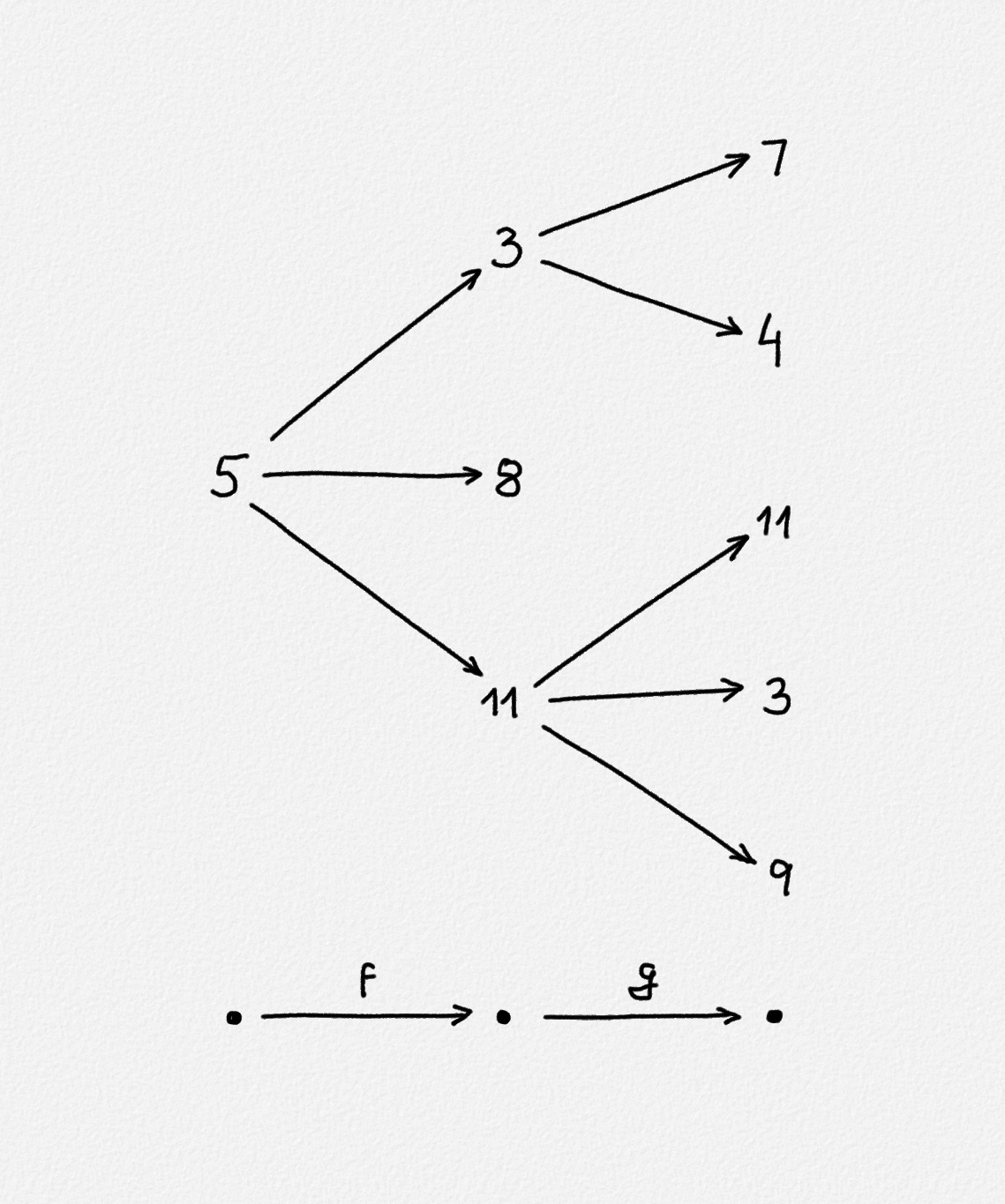
Non-deterministic function composition — An example where applying a function `f` to `5` produces any of the values `3`, `8` or `11`. Applying another function `g` to `3` produces `7` or `4`. Applying `g` to `8` produces no values at all. And applying `g` to `11` may produce the value `11`, `3` or `9`. The composition of `g` and `f` applied to `5` can then produce any of the values `7`, `4`, `11`, `3` or `9`, corresponding to any of the paths starting at `5` and ending at a node in the rightmost column.

Expressed using the list monad, we have `f 5 = [3, 8, 11]`, `g 3 = [7, 4]`, `g 8 = []`, `g [11] = [11, 3, 9]`, and `(f >>= g) 5 = [7, 4, 11, 3, 9] = concatMap g (f 5)`.

f >=> g may return any value that g may produce for any value that f might produce. As the figure suggests, we want to concatenate all the lists produced by mapping g over the list of values produced by f:

(f >=> g) x = concatMap g (f x)

Since x >>= f = (const x >=> g) (), this gives the definition x >>= f = concatMap f (const x ()) = concatMap f x. return x should produce a container containing x. So we define return x = [x]. This gives the following Monad instance for lists:²

instance Monad [] where
    return x = [x]              -- or return = singleton if you prefer
    x >>= f  = concatMap f x    -- or (>>=) = flip concatMap if you prefer

It would be possible to illustrate the use of the list monad to implement an NFA easily and elegantly in Haskell, but I think it is more instructive if we look at a simpler problem: navigating a maze.

This is an approximation because lists aren't sets. The order of the elements in a list matters. There is no order of the elements in a set. More importantly, a list can contain an element more than once. A set can't. This creates some wrinkles where implementing some non-deterministic computation using sets would be efficient but a naïve implementation using lists would take exponential time. Still, there are many examples where using lists to model non-deterministic computations is useful. ↩
In the section on list comprehensions, I gave you an exercise that asked you to implement concat as a list comprehension. This definition of concat is easily generalized to concatMap:
```
concatMap f xs = [y | x <- xs, y <- f x]
```
It turns out that the definition of (>>=) in the Monad instance for lists in the standard library does in fact use this list comprehension:
```
xs >>= f = [y | x <- xs, y <- f x]
```
↩