Recursive Types
Haskell has lists built right into the language, and we will see that they are ubiquitous in functional languages in general, exactly because their recursive definition—a list is empty or consists of an element followed by a list of the remaining elements—aligns very well with using recursion as the only tool to repeat things in functional languages.
Assume for now that there is no built-in list type in Haskell. How would we
define our own? Quite easily. We write down the inductive definition I just
gave, say to define a list of Ints:
data IntList
= Empty -- An integer list is empty or
| Cons Int IntList -- consists of an integer followed by the rest of the list,
-- which is itself an IntList
So it's perfectly fine to use a type itself in its own definition. The type definition is recursive.
In C, such a definition wouldn't work:
struct int_list {
int head;
struct int_list tail;
};
Clearly, this would mean that the int_list type has infinite size because
every int_list would have to contain within it a complete int_list. What we
can do in C is to define an int_list as storing the head of the list and
then pointing to the remainder of the list, which is itself an int_list
again:
struct int_list {
int head;
struct int_list *tail;
};
These pointer shenanigans aren't necessary in Haskell, nor are they in Python, Java, and many other modern languages:
class IntList {
// A whole bunch of methods omitted
int head;
IntList tail;
};
Can you guess why? C uses a value model of variables. If we define something
to be an int_list, then it is an int_list, the whole list is stored in the
variable itself. Haskell, Java, and Python use a reference model of
variables,1 which means that variables themselves only store pointers to
values, and the values themselves are stored on the heap. This ensures that an
IntList object has constant size even if the list it represents can be
arbitrarily large. As the following figure illustrates, an IntList is really
just a single list node that stores two pointers, one to the value the list node
"stores", and one to the remainder of the list.
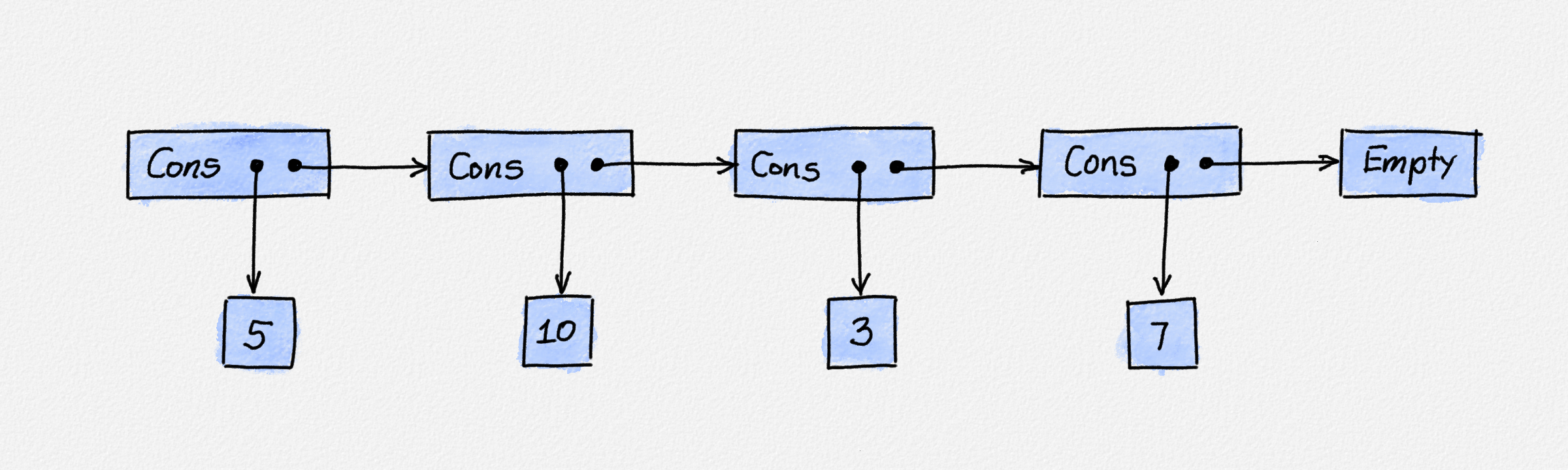
The in-memory representation of the list
Cons 5 (Cons 10 (Cons 3 (Cons 7 Empty))).
Now that we have our IntList type, we can use its data constructor as patterns
and implement a whole bunch of useful list functions:
intListHead :: IntList -> Int
intListHead Empty = error "Cannot take the head of an empty list"
intListHead (Cons x _) = x
To retrieve the head of a non-empty list, we return the element that is, well,
stored at the head. Taking the head of an empty list gets us into trouble
because this list doesn't have a head by definition. Not knowing about the
Maybe type yet, the best we can do is to raise an error using Haskell's
built-in error function.
Taking the tail of a list works analogously:2
intListTail :: IntList -> IntList
intListTail Empty = error "Cannot take the tail of an empty list"
intListTail (Cons _ xs) = xs
Let's look at two more insteresting examples, both of which we will develop to
their full generality in the next chapter. The first one is a function that
transforms an IntList into a new IntList by applying some function to every
element:
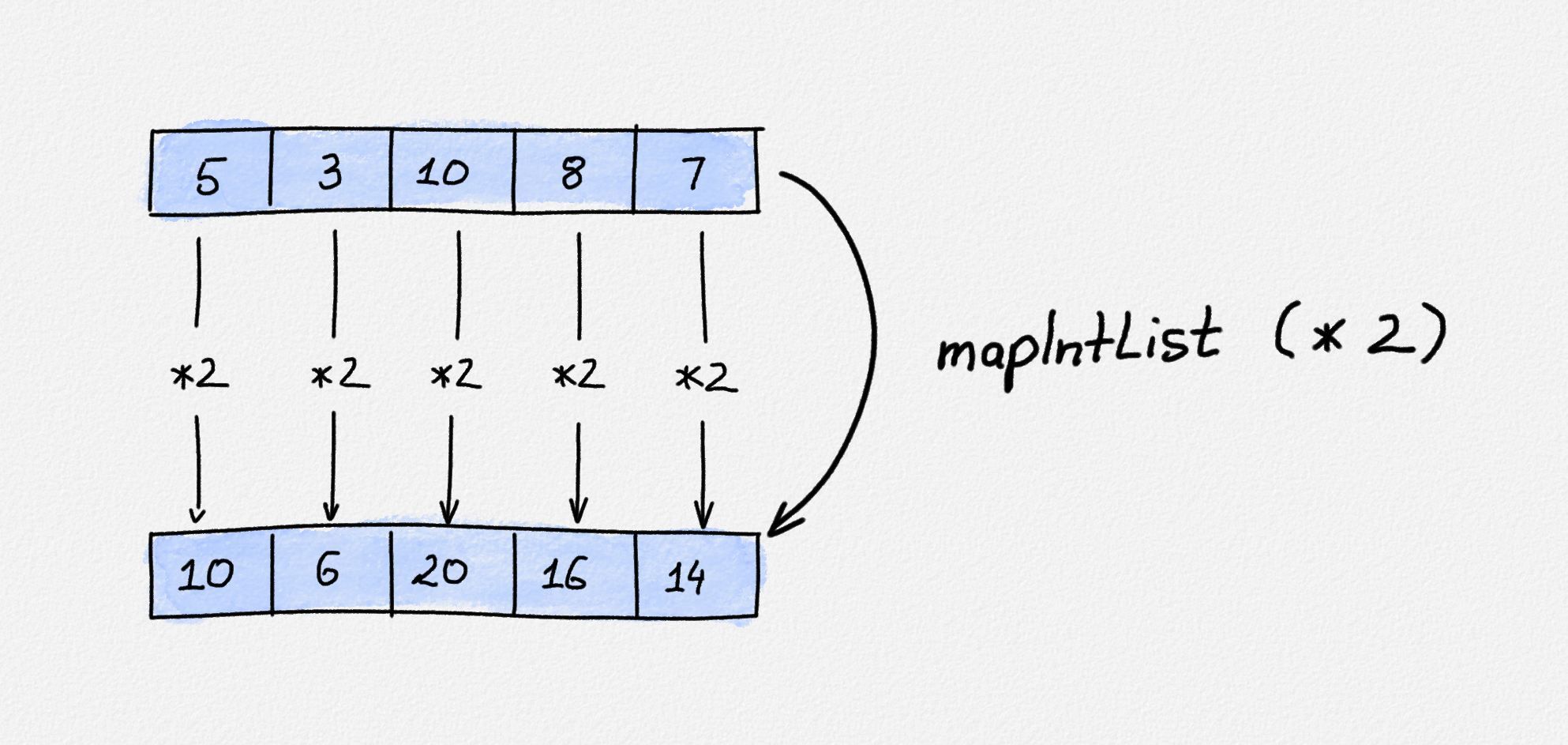
Illustration of
mapIntList (* 2) (Cons 5 (Cons 3 (Cons 10 (Cons 8 (Cons 7 Empty))))). Each
list element is multiplied by 2.
How do we construct the list this function should produce?
-
If the list is empty, then the result should also be empty. There are no list elements to which we could apply our function.
-
Otherwise, we should start by applying the function to the head of the list. This gives the head of the output list. The remainder of the output list is then obtained by applying the function recursively to all elements in the tail of the input list.
This translates directly into the following definition:
mapIntList :: (Int -> Int) -> IntList -> IntList
mapIntList _ Empty = Empty
mapIntList f (Cons x xs) = Cons (f x) (mapIntList f xs)
Using an inner function to avoid excessive passing around of function arguments, this definition becomes:
mapIntList :: (Int -> Int) -> IntList -> IntList
mapIntList f = go
where
go Empty = Empty
go (Cons x xs) = Cons (f x) (go xs)
Both implementations produce the same result, but the latter is more idiomatic and slightly faster.
As a second example, let's develop a function that filters a list. More precisely, it produces a list containing only the elements from the input list that match some condition:
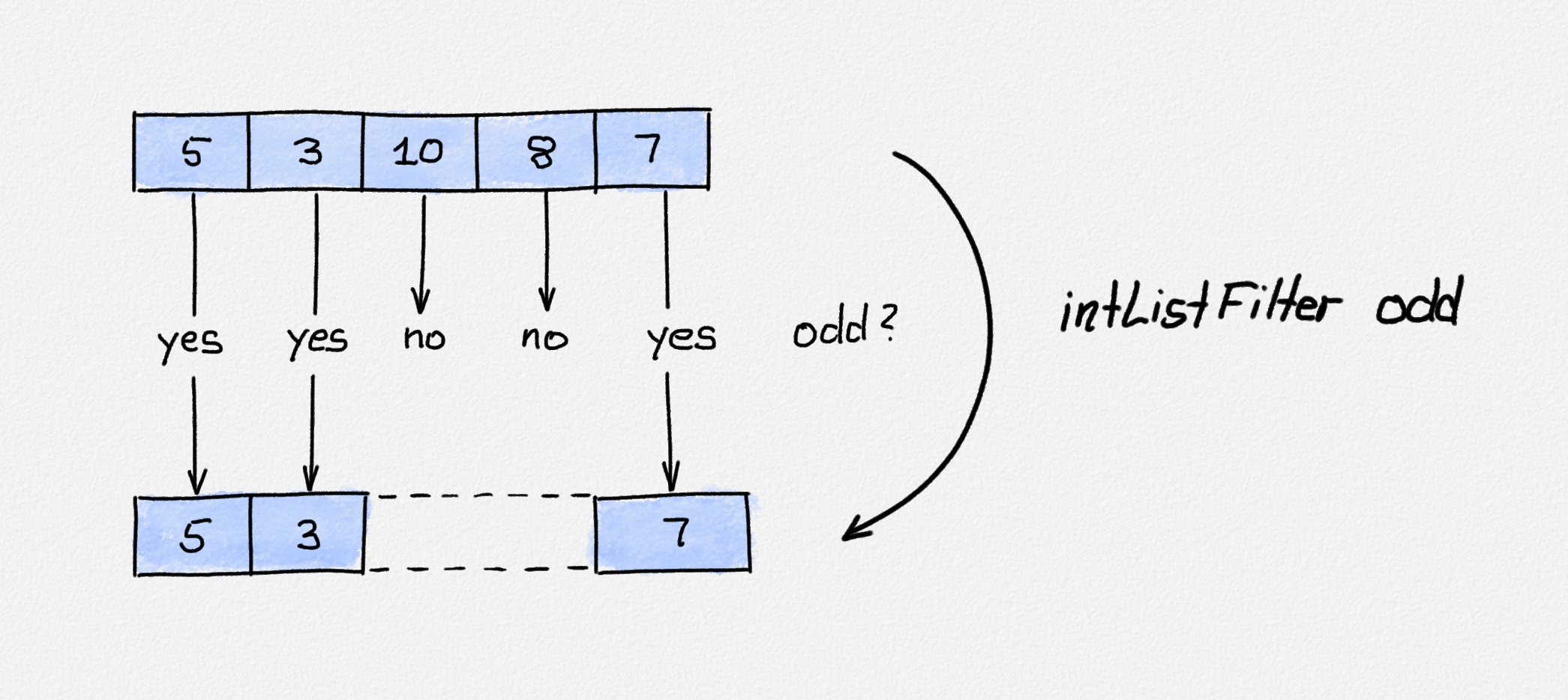
Illustration of
intListFilter odd (Cons 5 (Cons 3 (Cons 10 (Cons 8 (Cons 7 Empty))))). Only
the odd elements are kept in the output list. Note that the gap in the output
list is there only for illustrative purposes, to make the elements of the input
and output lists line up. The output list is simply
Cons 3 (Cons 3 (Cons 7 Empty)).
Again, we can define this function recursively:
-
Filtering an empty list produces an empty list because there are no elements that could satisfy the predicate.
-
If the list is non-empty and the first element
xof the list satisfies the predicate, thenxis also the first element in the filtered list. The remainder of the filtered list contains all elements of the tail that satisfy the predicate, which we produce by filtering the tail recursively. -
If the first list element does not satisfy the predicate, then it's not part of the filtered list. Thus, all elements of the filtered list must come from the tail, and we can produce the entire result by filtering the tail recursively.
intListFilter :: (Int -> Bool) -> IntList -> IntList
intListFilter pred = go
where
go Empty = Empty
go (Cons x xs) | pred x = Cons x (go xs)
| otherwise = go xs
Exercise
Implement a function that returns the length of an IntList:
intListLength :: IntLIst -> Int
>>> intListLength Empty
0
>>> intListLength (Cons 5 (Cons 1 (Cons 0 Empty)))
3
Solution
For an obvious but inefficient solution, the trick is to think recursively:
- The empty list has length 0.
- A non-empty list has length one more than the length of its tail.
Since the tail is itself an
IntList, we can find this length by callingintListLengthon the tail recursively
intListLength Empty = 0
intListLength (Cons _ tail) = 1 + intListLength tail
The problem with this implementation is that it's not tail-recursive. To
obtain a tail-recursive implementation, we can think about the problem
slightly differently: Let's say we want to implement a function
intListLengthPlus, which takes as argument an integer x and an
IntList ys. The goal of intListLengthPlus is to compute the sum of
x plus the length of ys. Then, clearly,
intListLength = intListLengthPlus 0
intListLengthPlus is useful because it can be implemented
tail-recursively:
- If
ys = Empty, thenintListLength x ys = x(asyshas length 0). - If
ys = Cons _ ys', thenintListLength x ys = intListLength (x + 1) ys', becauseyshas one more element thanys'.
Thus, we obtain the following tail-recursive implementation of
intListLengthPlus:
intListLengthPlus x Empty = x
intListLengthPlus x (Cons _ ys) = intListLengthPlus (x + 1) ys
Putting it all together, we obtain
>>> :{
| data IntList = Empty | Cons Int IntList
|
| intListLength = intListLengthPlus 0
| where
| intListLengthPlus x Empty = x
| intListLengthPlus x (Cons _ ys) = intListLengthPlus (x + 1) ys
| :}
>>> intListLength Empty
0
>>> intListLength (Cons 5 (Cons 1 (Cons 0 Empty)))
3
Exercise
The standard library contains a function splitAt for Haskell lists.
Implement the same function for IntLists:
splitIntListAt :: Int -> IntList -> (IntList, IntList)
Here is how it should behave:
-
splitIntListAt i xsshould splitxsinto two lists, one containing the firstielements inxsand one containing the remaining elements inxs. -
If
xshas fewer thanielements, then the first list in the pair returned bysplitIntListAtshould simply bexs, and the second list, the remainder, should be empty.
Solution
We can once again describe the result of splitting a list recursively.
Let the two resulting lists be ys and zs: intList i xs = (ys, zs).
-
If
xs = Empty, thenys = Emptyandzs = Empty, no matter whatiis. -
If
i = 0, thenysshould be empty, since it should contain the first 0 elements inxs, and consequently,zscontains all elements inxs,zs = xs. -
If
i > 0andxs = Cons x xs', thenyscontainsxand the firstx - 1elements inxs', whereaszscontains the remaining elements inxs'.
This translates into the following implementation:
splitIntListAt _ Empty = (Empty, Empty)
splitIntListAt 0 xs = (Empty, xs )
splitIntListAt i (Cons x xs) = (Cons x ys, zs )
where
(ys, zs) = splitIntListAt (i - 1) xs
Most of the exercises in this book are optional, unless I make them assignment questions. The next one is not. You should at least read it and, even if you don't attempt it, read the solution. The solution explains a useful feature of pattern matching that we haven't discussed before and which I will use in some of the code examples in the remainder of this book.
Exercise
Implement Merge Sort for IntLists:
mergeSort :: IntList -> IntList
As a reminder, here is the imperative description of Merge Sort:
-
If the input list has size less than 2, it is already sorted. Do nothing in this case.
-
If the input list has size at least 2, then recursively sort the left and right half and merge the two resulting sorted lists.
Merging two sorted lists is accomplished by repeatedly comparing the first
two elements of the two sorted lists. Let's call the two lists to be merged
L and R, and their two first elements x and y. Then, since L and
R are sorted, the smaller of x and y is the smallest of all the
elements in L and R. Thus, if x <= y, we remove x from L and add
it to the merged list. If y < x, we remove it from R and add it to the
merged list. Once one of the two input lists becomes empty, we append the
remaining elements in the other list to the merged list. I will not prove
here that this algorithm is correct. Hopefully, you do this in CSCI 3110 or
some other course where you see Merge Sort for the first time.
Here, our focus is on translating this into a functional implementation. I
hope you don't have any trouble with implementing mergeSort in terms of
merge :: IntList -> IntList -> IntList
which takes two sorted lists to be merged and returns the result of merging
them. To implement mergeSort, you need merge and a function to split a
list into its left half and right half. The latter shouldn't be that hard to
implement using the intListLength and splitIntListAt functions from the
previous two exercises.
The implementation of merge relies on describing the result of
merge xs ys inductively again:
-
If
xs = Empty, then there is nothing to mergeyswith, so the result is justys. -
If
ys = Empty, then there is nothing to mergexswith, so the result is justxs. -
Now assume that
xs = Cons x xs'andys = Cons y ys'. Then the result depends on the comparison ofxandy:-
If
x <= y, thenxis the first element in the merged list:merge xs ys = Cons x zs. The remainder of the merged list,zs, is obtained by mergingxs'andys. -
if
y < x, thenyis the first element in the merged list:merge xs ys = Cons x zs. The remainder of the merged list,zs, is obtained by mergingxsandys'.
-
Solution
Here's the implementation of mergeSort that I would have expected you
to come up with:
mergeSort :: IntList -> IntList
mergeSort Empty = Empty -- List is empty
mergeSort (Cons x Empty) = Cons x Empty -- List has one element
mergeSort xs = merge (mergeSort ls) (mergeSort rs)
where
(ls, rs) = splitIntListAt (intListLength xs `div` 2) xs
The implementation of merge based on the above description is
merge :: IntList -> IntList -> IntList
merge Empty ys = ys
merge xs Empty = xs
merge (Cons x xs) (Cons y ys)
| x <= y = Cons x (merge xs (Cons y ys))
| otherwise = Cons y (merge (Cons x xs) ys )
There are two issues with these implementations. Let's take them one at
a time. First, it's a little inelegant, and somewhat inefficient, to
take a list apart into its components and then build another list with
exactly the same components. We do this a lot in this implementation.
The second equation of mergeSort pattern matches against the pattern
Cons x Empty, thereby breaking a one-element list into its head x
and the empty tail, and then rebuilds the list from these components.
Similarly, the last equation of merge breaks both input lists into
head and tail, and the two recursive calls rebuild one of the lists from
its parts, as it needs to be passed to the recursive call unaltered.
With the tools I have taught you so far, this is the only thing we can
do, but there's a better way:
Haskell has a neat little thing called "at-patterns", because they use
the @ symbol. It's best to explain this using an example:
mergeSort :: IntList -> IntList
mergeSort Empty = Empty
mergeSort xs@(Cons _ Empty) = xs
mergeSort xs = merge (mergeSort ls) (mergeSort rs)
where
(ls, rs) = splitintListAt (intListLength xs `div` 2) xs
The interesting part is the second equation:
mergeSort xs@(Cons _ Empty) = xs
Remember that when matching a function argument against a variable, the
matching always succeeds, and the argument is assigned to the variable.
We can also match against data constructors to inspect the contents of a
function argument. At-patterns allow us to do both at the same time. The
equation mergeSort xs@(Cons _ Empty) matches only if the list has one
element, just as if we had written mergeSort (Cons _ Empty). However,
pattern matching also assigns the whole list to xs, so we can refer to
it on the right-hand side. In particular, we avoid rebuilding xs from
its parts. So, at-patterns allow us to match an argument (or part of an
argument) against a variable while at the same time inspecting its
contents using a data constructor pattern.
This idea also allows us to improve the implementation of merge:
merge :: IntList -> IntList -> IntList
merge Empty ys = ys
merge xs Empty = xs
merge xs@(Cons x xs') ys@(Cons y ys')
| x <= y = Cons x (merge xs' ys )
| otherwise = Cons y (merge xs ys')
Here, the last equation matches both arguments against Cons x xs' and
Cons y ys' to gain access to the head and tail of each input list. We
need them for the comparison x <= y. However, it also assigns the two
lists in their entirety to xs and ys. This allows us to say that if
x <= y, then we make x the first element in the merged list, and the
tail of the merged list is produced by merging the tail of xs, xs',
with the entirety of ys. If y < x, then the first element in the
merged list is y, and the tail of the merged list is produced by
merging xs in its entirety with the tail of ys, ys'.
The second issue with the implementation of mergeSort we have
developed so far irks the algorithms person in me: It's inefficient. The
problem is the use of intListLength and splitIntListAt to split the
list in half. intListLength walks down the entire list to be sorted to
determine its list, and splitIntListAt walks down the first half a
second time to split the list. We can't address this using IntLists.
We'll return to this issue after making lists polymorphic in the next
section.
-
Python, being dynamically typed, has no choice really. If we can store anything we want in a variable, the variable cannot store all these possible values by value. The only way to make variables have a fixed size in dynamically typed languages is by storing only references to values in variables, and the values themselves live on the heap. ↩
-
You should read the use of
xsin this definition as being the plural ofx. If the first element of a list is anx, then the elements stored in the tail of the list is a bunch ofxs. This naming of variables is quite common in the Haskell world. Some authors even go as far as definingxss, which is a collection ofxs, that is, each element in this collection is itself a list ofxs. Once you're used to this naming, it feels quite natural, and I'd defend thexvsxsnaming; the extension toxssmay be more questionable. ↩