Thunks
Before looking at another use of lazy evaluation—infinite data structures—let me try to take the mystery out of lazy evaluation by discussing how it is implemented. This will also shed some light on why it is more costly than applicative order evaluation.
When using applicative order evaluation, all we ever pass around between function calls is values. Normal order evaluation passes around unevaluated expressions, and these expressions need to be stored in memory somehow.
Let's start by pretending that Haskell uses normal order evaluation. Then primitive values (numbers and characters) are stored as they are. Expressions are built up using function application. Remember, operators are just a special kind of two-argument functions. In memory, we represent such a function application as a record that stores pointers to the function to be applied as well as pointers to the expressions that are the arguments of the function:
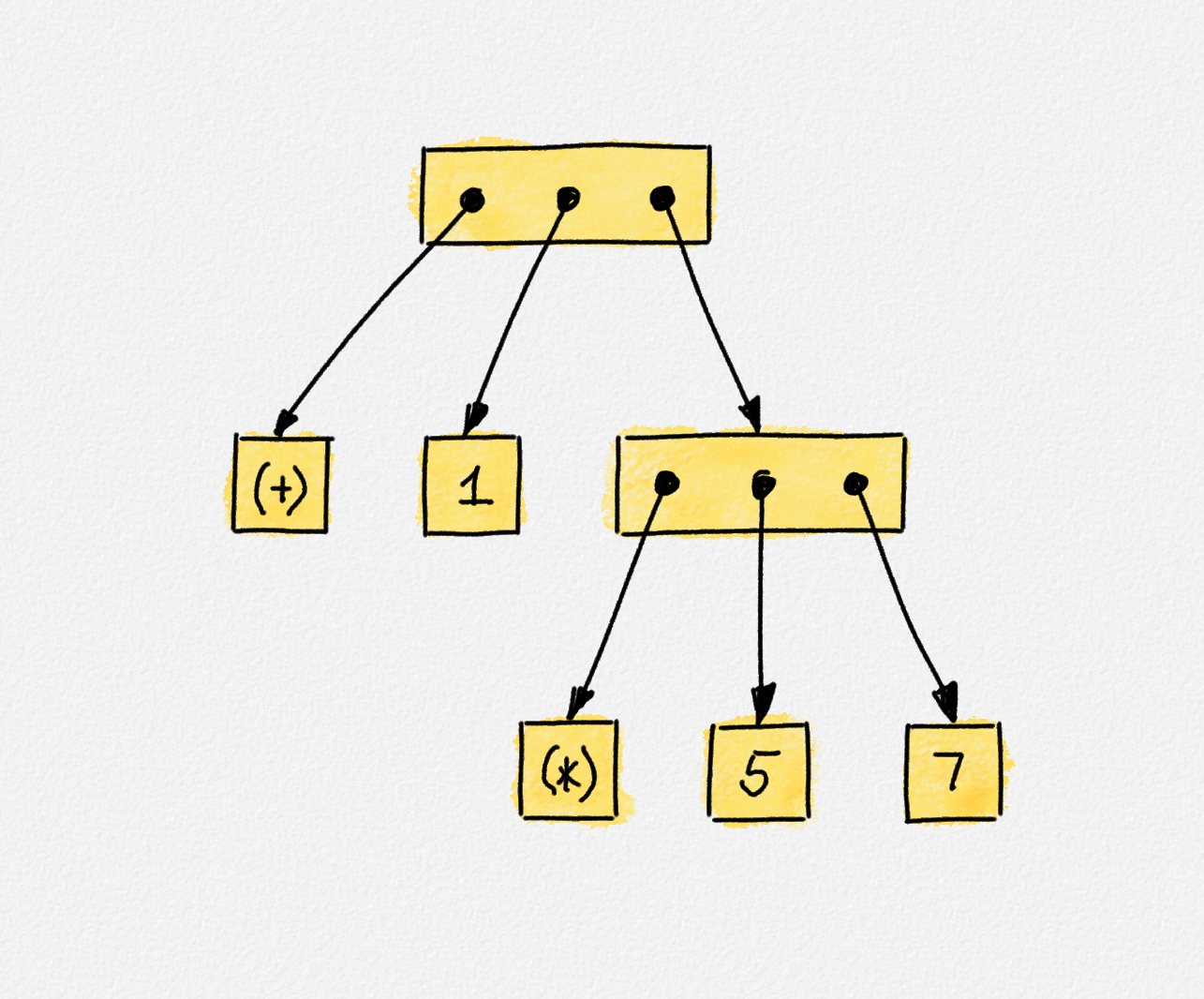
The expression tree for the expression 1 + 5 * 7. Note
that + and * are just ordinary functions in Haskell, so the expression tree
contains a function call for each of two arithmetic operations.
These expressions can of course themselves be function applications, so we really get a whole expression graph. Also, the function to be applied may itself be produced by an expression, so even the pointer to the function to be applied points to an expression.
The reason why we get an expression graph, not an expression tree is because local variables allow us to share subexpressions. Consider the following expression:
filter (uncurry (<)) $ zip xs (tail xs)
where xs is a list of numbers. Then the expression graph nodes for zip and
tail both refer to xs as their arguments, as shown in the following figure.
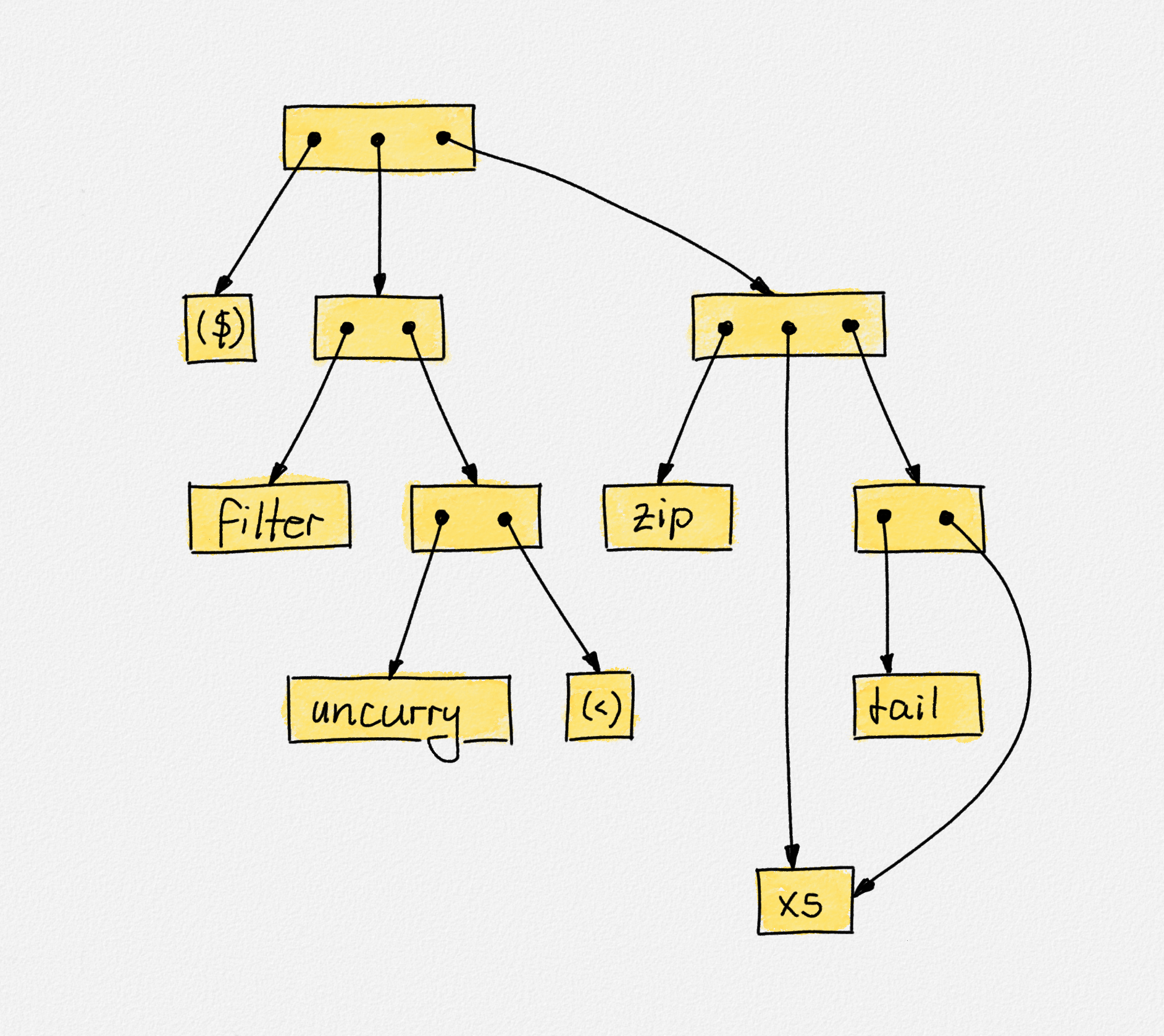
The expression graph for the expression
filter (uncurry (<)) $ zip xs (tail xs)
For normal-order evaluation, this details is unimportant. For lazy evaluation, it is imortant because sharing a subexpression means that the subexpression is evaluated only once even if it occurs multiple times in a bigger expression.
If we use normal-order evaluation, then every time we need to know the value of an expression, we traverse the expression graph and build up the value of the whole expression from the values of its subexpressions. When I say "we" here, I mean the runtime system of the programming language.
Now how do we bolt lazy evaluation onto this? It's fairly easy really.1 Each expression graph node gets replaced with a thunk.2 A thunk can store one of two things:
- An expression graph node or
- A value in WHNF.
When using pattern matching, the expression to be matched against each pattern is represented as a thunk—all values in Haskell are thunks. If we match against a variable or wildcard, then there is no need to evaluate the thunk. In this case, pattern matching simply makes the variable point to the thunk. If we match against a pattern that uses a data constructor, then one of two things happens:
-
If the thunk already stores a value in WHNF, then we can check whether the data constructor of the pattern matches the data constructor of the WHNF expression stored in the thunk.
-
If the thunk stores an expression graph node, then we evaluate the expression represented by this node just enough to turn it into a WHNF value. We replace the expression graph node in the thunk with this value and then proceed to matching the data constructor of the thunk to the data constructor of the pattern in the same way as when the thunk already stored a value in WHNF.
Note that when the data constructor of an expression takes arguments, these arguments are themselves represented as thunks, so a thunk in WHNF stores pointers to other thunks that represent the arguments of the data constructor. This is how we get partial expression evaluation: When matching subexpressions to patterns, we apply the same logic as above to decide which subexpressions need to be transformed into WHNF. For every subexpression that is converted to WHNF, we store the WHNF value in the thunk to ensure that we do not evaluate the subexpression again if we need to know its value a second, third or 100th time. Again, when I say "we", I mean the Haskell runtime system, which implements this logic for us under the hood.
Look again at our implementation of (&&):
(&&) :: Bool -> Bool -> Bool
False && _ = False
_ && y = y
We now have the language to explain exactly how this implementation behaves. To
evaluate the expression x && y, we first transform x into WHNF to reveal its
data constructor. So x's thunk now stores True or False, because these are
the only data constructors of the Bool type. We match the data constructor
against False. If it is False, then we return a different thunk storing
False, without forcing any evaluation of y's thunk. If x is True, then
we use the second equation. This equation matches x to the wildcard and y to
the variable y, so no evaluation of thunks is required. We then return y's
thunk as the result. In particular, if y's thunk was not evaluated before
evaluating the expression x && y, then y remains unevaluated and is
evaluated only when the caller pattern matches the result of x && y against
True or False. If y's thunk has already been evaluated, then it stores a
value in WHNF, so the result of x && y is also in WHNF.
Note that the following implementation exhibits essentially the same behaviour:
(&&) :: Bool -> Bool -> Bool
True && y = y
_ && _ = False
To evaluate x && y, we need to convert x into WHNF and then check whether
the data constructor is True. If it is, the result is y's thunk, whether it
is already in WHNF or not. If x is False, then the first equation does not
apply, and the second equation defines the value of x && y to be False,
without evaluating x or y further.