Weak Head Normal Form
For Boolean expressions, it is a binary decision whether we evaluate it or not. We either need to know its value or we don't. The same is true for numerical values and characters. For all other types, there is the possibility to evaluate expressions only partially. To understand how this works, and how much of an expression is evaluated, we need to learn about a terribly formal-sounding but ultimately rather natural concept called weak head normal form.
An expression is in weak head normal form (WHNF) if
Its type is a primitive type (number or character) and the expression has been fully evaluated or
Its type has been defined using
dataornewtypeand the expression has been evaluated enough to determine its data constructor. The arguments of the data constructor may be unevaluated.
You should think of a Haskell program as a giant unevaluated expression we're
constructing using the equations in our program. When we run this program, we
ask for the value of the whole program. At this point, we need to evaluate some
of the subexpressions used to build the whole program. Since the whole program
is composed of functions and the means to evaluate functions is pattern
matching, it is pattern matching that determines which subexpressions of the
whole program expression need to be evaluated. Consider a function f x, which
may be implemented using multiple equations or, equivalently, using a case
expression. Our program tries the equations or branches of the case expression
in order until it finds the first branch that applies, and it uses pattern
matching to do so.
-
If the pattern is a variable or wildcard, then this pattern always matches. No evaluation of
xis necessary to decide this. -
If the pattern involves a data constructor, the expression passed to
fas an argument is evaluated enough to bring it into WHNF. This data constructor may take arguments, each of which is represented as a subpattern. Each such subpattern may itself be a variable or involve a data constructor. To match these subpatterns, we apply the same two rules—not evaluating sub-expressions matched to variables and wildcards and evaluating data constructor patterns to WHNF—recursively to these subpatterns.
Subpatterns are matched from left to right. Thus, if we have a data type
data Pair a b = Pair a b
and a function we need to evaluate uses the pattern
Pair (Pair x 0) (Pair y z)
then matching this pattern proceeds as follows:
-
First the whole function argument is evaluated to WHNF, that is, it is brought into the form
Pair a b. -
Next
aneeds to be matched to the patternPair x 0, soais evaluated to WHNF bringing it into the formPair c d. -
cis matched toxwithout evaluating it further. -
dis evaluated to determine whether it is0. If it is not, then this is where evaluation stops because we know the pattern does not match no matter whatblooks like. At this point, there better be another equation for our function that can be tried next. -
If
dis0, then we need to matchbto the patternPair y z. Thus, we bringbinto WHNF,Pair e f.
_ e is matched to y without evaluating it further.
fis matched tozwithout evaluating it further.
Two comments are in order before we look at a few examples.
-
Remember that multi-argument functions are syntactic sugar for single-argument functions whose return values are themselves functions.
f x y z = ...is the same asf = \x -> \y -> \z -> .... This immediately implies that function arguments are evaluated left to right. First we evaluatexenough to find the first equation wherexmatches the first pattern. Then we evaluateyenough to test whetherymatches the second pattern of this equation. If it doesn't, then we need to go back and try to find another equation wherexmatches the first pattern. Again, we see whetherymatches the second pattern. If it does, we finally check whetherzmatches the third pattern. If it does, we have found the correct equation. If it doesn't, then we try the next equation, again evaluatingx, theny, thenzto see whether they all match their patterns. -
Pattern matching may involve pattern guards. These pattern guards are nothing but Boolean expressions. Thus, to determine whether an equation with a pattern guard matches, we evaluate these Boolean expressions using our standard pattern matching rules.
Now for a few examples, all involving lists. Remember that the built-in list
type in Haskell has two data constructors, [] and (:):
data [] a = [] | a : [a]
The standard library provides us with a function null to test whether the list
is empty. Here is its implementation:
null :: [a] -> Bool
null [] = True
null _ = False
This implies that null is a constant-time operation no matter how long the
list is. This is true even if the list has infinite length. We will look at
infinite data structures in the next section. Let's have a closer look. To
evaluate the expression null xs, we start by testing whether the first
equation of null applies. Since the pattern of this equation is [], a data
constructor, we need to evaluate xs enough to bring it into WHNF, to reveal
its data constructor. If xs = [], then the first equation matches, and the
result is True. If xs = y:ys, then the first equation does not match and we
try the second equation. This equation always matches because its pattern is the
wildcard. Thus, the result is False without the need to evaluate y and ys
further.
Let me emphasize a subtle point here: When matching against the data constructor
(:), all we test is that the list has a head and a tail. We don't care what
they look like. Either are evaluated only if we need to know more about them.
GHCi gives us a handy tool1 that lets us inspect exactly how much an expression has been evaluated so far:
>>> xs = [x+1 | x <- [1..10]] :: [Int]
>>> :sprint xs
xs = _
:sprint prints an expression without forcing any parts of it to be evaluated.
Parts of the expression that were evaluated before are shown. Any part of the
expression not evaluated yet is shown as _. Here, we just defined xs as the
list obtained by adding 1 to each element in the list of integers between 1 and
10, but we did not inspect it in any way yet. So no part of it has been
evaluated.
If we ask whether xs is empty, then xs gets evaluated to WHNF, and that's
all that happens:
>>> xs = [x + 1 | x <- [1..10]] :: [Int]
>>> null xs
False
>>> :sprint xs
xs = _ : _
This tells us that xs has a head and a tail. That's all null needed to know
to figure out that xs is not empty. Most importantly, it didn't even need to
know the value of the head, only that it exists. So :sprint prints
xs = _ : _, not xs = 2 : _.
If we ask for the value of xs head, then things change:
>>> head xs
2
>>> :sprint xs
xs = 2 : _
To print the value of head xs, GHCi had to evaluate it, so the head is now
stored in evaluated form.
Next, let's try to ask for the length of xs:
>>> length xs
10
>>> :sprint xs
xs = [2,_,_,_,_,_,_,_,_,_]
To compute length xs, GHCi had to walk down the entire list. Each list node
has been evaluated to figure out whether it represents the empty list ([]) or
is a "cons-cell" (_ : _). GHCi prints the list using bracket notation now
because it knows the shape of the whole list. If you count, you'll see that
the initial 2 is followed by 9 underscores, so xs is a 10-element list.
The 2 is shown by value because we evaluated it previously to print the value
of head xs. We haven't asked for the values of the remaining list elements.
length xs only needs to know that they are there, not what they are. Thus,
they are all still underscores.
What if we ask for the third list element but without printing it?
>>> y = head $ tail $ tail xs
>>> :sprint xs
xs = [2,_,_,_,_,_,_,_,_,_]
Huh. Shouldn't the result be xs = [2,_,4,_,_,_,_,_,_,_]? Not really. We only
defined that y should have the same value as the third element in xs. We
didn't ask for y's value. Thus, both y and the third element in xs remain
unevaluated. If we ask for y's value, then both y and the third element of
xs get evaluated because both y and xs point to this value in memory, as
shown in the following figure:
>>> y
4
>>> :sprint y
y = 4
>>> :sprint xs
xs = [2,_,4,_,_,_,_,_,_,_]
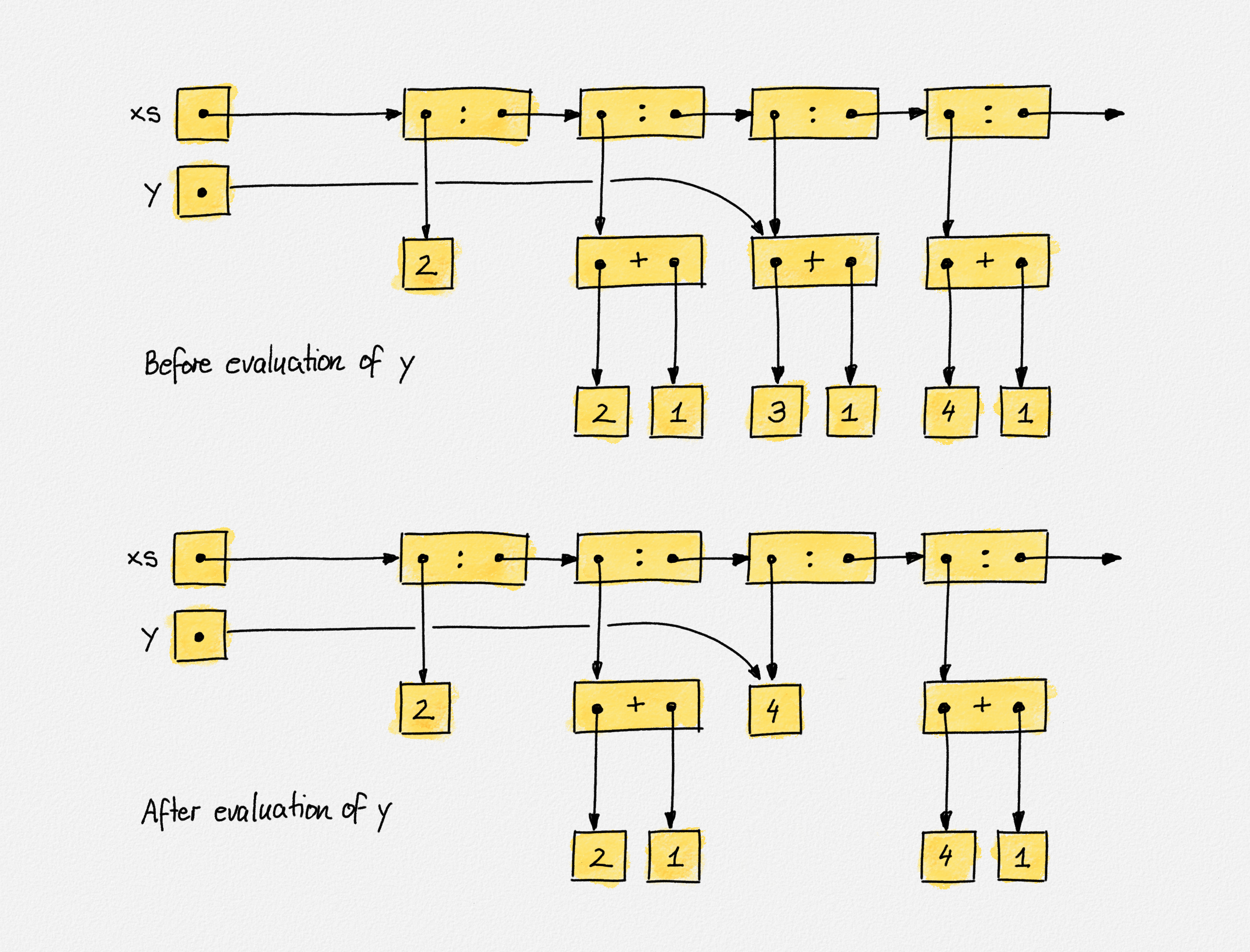
Haskell uses a reference model of variables.
Thus, every variable stores only a pointer to a thunk, which can be
either a value or an unevaluated expression.2 Assigning the third element
in xs to y only makes y and the third list node point to the same thunk,
an unevaluated expression at this point. Asking for y's value forces this
thunk to be evaluated: the expression stored in the thunk gets replaced with its
value. Since the third list node of xs points to the same thunk, the third
element in xs is now also shown as evaluated.
Asking for the values in xs to be evaluated, say by printing xs, leads to
all of them to be stored in evaluated form now:
>>> xs
[2,3,4,5,6,7,8,9,10,11]
>>> :sprint xs
xs = [2,3,4,5,6,7,8,9,10,11]
These examples also illustrate the difference between normal order evaluation
and lazy evaluation. With normal order evaluation, :sprint xs would produce
xs = _ after all of the steps above, because xs would always be stored in
unevaluated form, and we would evaluate those parts of xs needed to answer
each query every time we ask a query. With lazy evaluation, those parts of xs
that have been evaluated already are stored in evaluated form after evaluating
them for the first time.
Quirks of :sprint
There are some quirks to GHCi's behaviour that may be confusing and that I don't understand fully either. First, even if you force a number to be evaluated by asking for its value, GHCi will claim it has not been evaluated yet:
>>> x = 5
>>> x
5
>>> :sprint x
x = _
That's because numbers are polymporphic:
>>> :t x
x :: Num p => p
If GHCi were to update x's thunk (see next section) to store
x's value instead, it would have to commit to some type, because different
types have different representations in memory. If the context is not enough
to determine the ype of x, as is the case here, GHCi keeps x's thunk in
unevaluated form even if we print x's value. You normally don't run into
this behaviour in compiled Haskell code, but it does happen in GHCi, so I
thought it would be important to mention it.
If we force x to have a type, then everything works as expected:
>>> x = 5 :: Int
>>> x
5
>>> :sprint x
x = 5
Or so it seems. Even if we don't force x to be evaluated by asking for its
value, :sprint shows it in evaluated form:
>>> x = 4 :: Int
>>> :sprint x
x = 4
That's probably (I don't know exactly) because 4 is a constant. So, as an
optimization, the thunk representing 4 stores this value right from the
start instead of storing 4 as an expression to be evaluated.
The same happens with the empty list:
>>> xs = []
>>> :sprint xs
xs = []
If we try to work with an integer expression, everything works as expected:
>>> x = 1 + 2 :: Int
>>> :sprint x
x = _
>>> x
3
>>> :sprint x
x = 3
Let's try this function:
atLeastTwo (_:_:_) = True
atLeastTwo _ = False
It returns True if its arument is a list with at least two elements.
Otherwise, it returns False. Fully parenthesized, the definition should be
written like this:
atLeastTwo (_:(_:_)) = True
atLeastTwo _ = False
Now if we call atLeastTwo [1,2,3,4], then we try the first equation first. To
check whether this equation applies, we first need to check whether the argument
was constructed using the data constructor (:). Thus, we evaluate the list to
the form <1> : <[2,3,4]>. (I use <x> here to refer to an unevaluated
expression with value x.) But that's not enough. To match the pattern, the
tail of the list must itself be of the form (_:_). So we need to evaluate the
tail of the list to WHNF, which gives us the expression <1> : (<2> :
<[3,4]>). At this point, we see that the argument has the right form—it is
composed of at least two elements—and the first equation applies, we return
True. This shows that atLeastTwo does not evaluate the list beyond the first
two elements. Calling atLeastTwo with a two-element list takes just as long as
calling it with a 10-million-element list. It also shows that even the first two
elements of the list are not evaluated. The pattern includes wildcards for these
elements, so our rule says that we do not need to evaluate them; we only check
that they exist.
Again, we can try this all out in GHCi:
>>> :{
| atLeastTwo (_:_:_) = True
| atLeastTwo _ = False
| :}
>>> xs = [x + 1 | x <- [1..10]] :: [Int]
>>> atLeastTwo xs
True
>>> :sprint xs
xs = _ : _ : _
Indeed, GHCi evaluates xs enough to verify that it matches the pattern
_:_;_, and it does not evaluate any of the list elements. [1..] is the
infinite list of all positive integers. We can try that atLeastTwo evaluates
only as much of it as it needs to know that this list has at least two elements:
>>> xs = [1..] :: [Int]
>>> atLeastTwo xs
True
>>> :sprint xs
xs = 1 : 2 : _
To understand why the first two elements of xs are shown in evaluated form
now, read the info box on "Quirks of :sprint" above.
One more example:
secondElementIfZero [0, x] = x
secondElementIfZero _ = 0
This is syntactic sugar for
secondElementIfZero (0 : (x : [])) = x
secondElementIfZero _ = 0
This function returns the second element of a list if the list has exactly two
elements and the first element is 0. First let's call secondElementIfZero
[0, 5]. We need to check whether the first equation applies. So we need to
check whether the list is of the form x : xs. This evaluates [0, 5] to the
form <0> : <[5]>. We need to check whether the first elemen is 0. This
evaluates the list to 0 : <[5]>. We need to check whether the tail of the list
is of the form x : []. This evaluates the list to 0 : (<5> : <[]>). Finally,
we need to know whether the tail of the tail is the empty list. This evaluates
the list to 0 : (<5> : []). At this point, we conclude that the first equation
applies and we return the second element of the list. Note that we leave x
unevaluated. Thus, while secondElementIfZero extracts the second list element,
it actually returns it as an unevaluated expression if it was not evaluated
before.
Again, we can try this out in GHCi:
>>> :{
| secondElementIfZero [0, x] = x
| secondElementIfZero _ = 0
| :}
>>> xs = [0,5] :: [Int]
>>> secondElementIfZero xs
5
>>> :sprint xs
xs = [0,5]
>>> xs = [x + 1 | x <- [1..10]] :: [Int]
>>> secondElementIfZero xs
0
>>> :sprint xs
xs = 2 : _
The last example shows that, due to the interpretation of the pattern [0,x] as
0:(x:[]), the conditions of this pattern are checked in this order:
- The argument has a head and tail.
- The head is 0.
- The tail has a head and tail.
- The tail of the tail is empty.
As soon as one of these conditions fails, we know that the first equation does
not match, and the argument is not evaluated any further. The list xs in the
last example was of the form [2,3,4,5,6,7,8,9,10,11]. Thus, it passed the
first test but failed the second. The third and fourth test are no longer
performed. :sprint tells us that xs was evaluated to a cons-cell _:_ whose
head was fully evaluated to 2, but the tail was left unevaluated.
-
For most of your current efforts at programming in Haskell, you can ignore
:sprint, because you won't care whether something is evaluated lazily or eagerly. Once you reach the point where you write code that relies on not being lazy—for performance reasons—or on being lazy—because the strict version would hang,:sprintcan be a useful investigative tool. ↩ -
The term "value" is a bit misleading here. A thunk always stores either a function call or a data constructor. The former is exactly what an unevaluated expression is: some function call which, when executed, produces the value represented by the thunk. The latter is how Haskell stores data. Such a data constructor can simply be a value, such as
5,FalseorTrue, or it can store references to other thunk if the data constructor takes arguments. For example, the data constructor(:)for lists takes two arguments, the head and tail of the list. An evaluated list thunk thus stores this data constructor along with two pointers to thunks that represent the head and tail of the list. Those thunks may be stored in evaluated or unevaluated form, depending on whether we already needed to know their values. ↩