Symbiosis as a metaphor for Hierarchical Policy Search in Genetic Programming:
One of the early developments in (biological) evolution resulted in the transition from prokaryotes to eukaryotes. At the centre of symbiosis lies the ability of organisms (bacteria) to inherit material from different species of organism. Thus, for symbiosis to actually take place, the context of the inherited material -- candidate symbiont -- w.r.t. that of the `host' organism must be clearly established. Models of symbiosis therefore pay considerable attention to how host `compartments' control symbiont content.A set of five factors appear to play a significant role in establishing frameworks for symbiosis: Spatial relation between potential symbionts; Temporal relationships between host `compartment' and candidate symbionts; Metabolic or the mechanism for communication between symbionts; Genetic or the process by which alignment of genetic material is established; and the nature of the Coevolutionary relationship, where a mutualistic relation is often assumed, but this might actually have began as an openly adversarial relation and over time became mutualistic.
- Heywood and Lichodzijewski
(2010) provides a wider review of symbiotic metaphors in Evolutionary Computation.
- EvoComplex 2010 Slides
Framework for Symbiotic Evolution in Genetic Programming
In order to get to this point, however, there are several general evolutionary systems concepts that need to be available to successfully support the scaling of Evolutionary Computation paradigms to real-world problem domains. Specifically, a major contributing factor to supporting diversity in (biological) evolution is the environment in which evolution takes place. Thus, as the wider `ecosystem' changes, different traits are favoured in the population of organisms. This concept also implies that the organisms are competing with each other to establish their respective niches. Natural selection will then select the appropriate survivors. From a learning system perspective this means that we have a `point' population that defines the cases against which evaluation of the candidate (host) population of organisms takes place. The interaction between point and host populations is that of a competition a.k.a competitive coevolution. From the perspective of a biological ecosystem this represents a major mechanism for speciation (in the host population) as in the definition of geographic barriers (dichopatric speciation) or the isolation of founder populations (peripatric speciation) to name but two. From a machine learning perspective, without speciation, we curtail our ability to support (automatic) problem decomposition. Without a point population we will need to evolve the host organisms over the some `complete' set of training instances -- where this is generally infeasible in practice or at least very in efficient.From an Evolutionary Computation perspective the mechanism governing the interaction between point and host population might be as simple as stochastic sampling of states defining the world, or as complex as a pair-wise Pareto optimal policy of replacement (the later unfortunately being rather expensive computationally). The principle factor in distinguishing which policy for competitive coevolution to adopt appears to be the informativeness of the cost function expressing the relative performance of hosts relative to the test conditions defined by the point population. The more (less) informative the cost function the more (less) appropriate stochastic sampling becomes.
- See for example Lichodzijewski
and Heywood (2009) for an example of this under reinforcement learning.
- Artificial Evolution 2009 slides
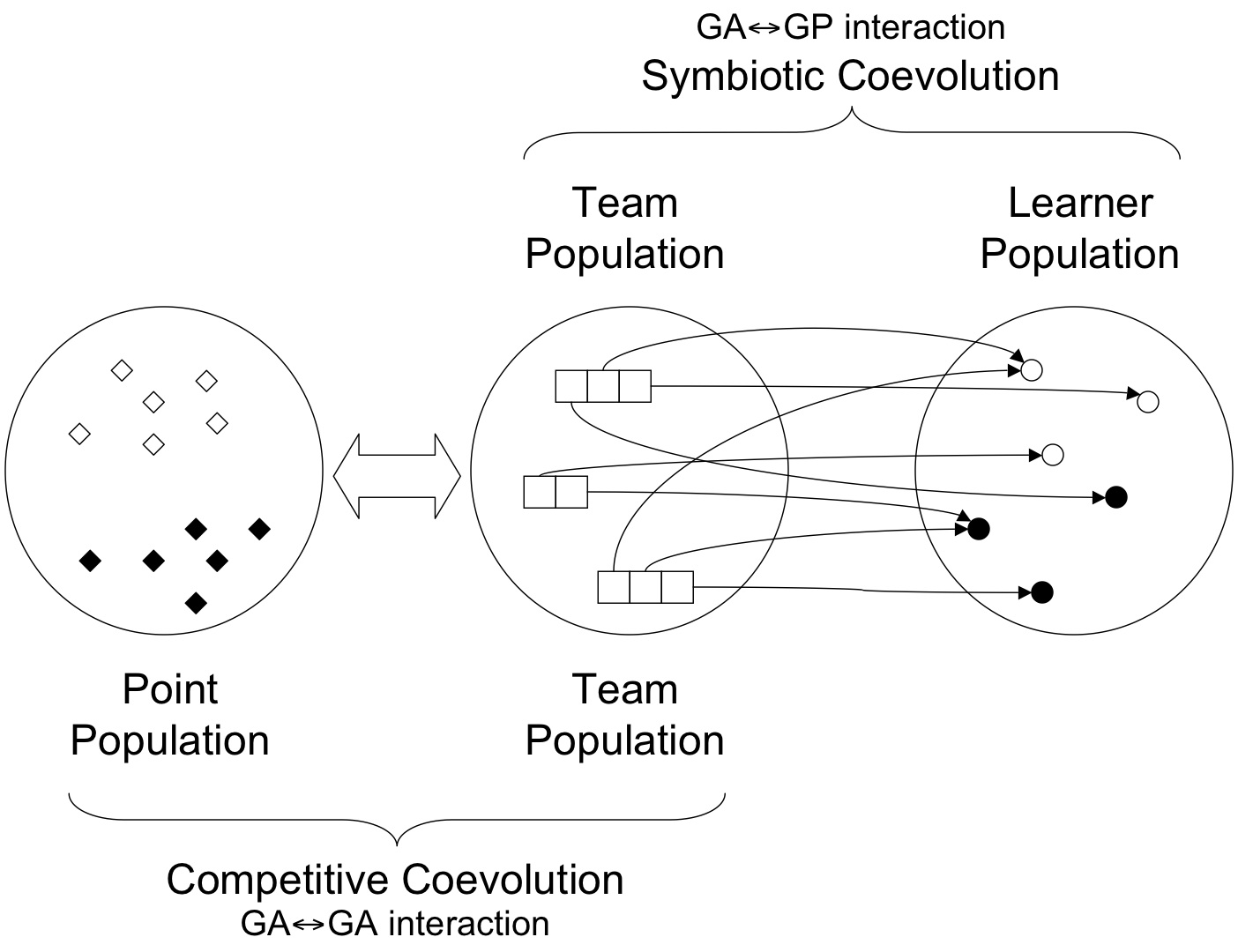
In essence, symbionts are initialized with a single `atomic' action, defined a priori relative to the problem domain. Thus, under a classification contact symbiont actions are sampled from the set of class labels. This implies that a host must consist of at least two symbionts with dissimilar actions in order to provide a non-degenerate behaviour. Moreover, the symbiont actions are NOT evolved. Instead, the goal of symbionts is to evolve a program representing a bidding policy. The bidding policy establishes the context under which the symbionts' action is employed. This naturally assumes a model of coevolution between symbionts based on cooperation. At the host level, the goal is to evolve the combination of symbionts which identify a `fit' host relative to others in the host population. Given a training scenario defined by the point population -- say, exemplar for classification -- symbionts from the same host run their respective bidding algorithms. Only the host symbiont with largest bid gets to suggest their action. It is relative to this action that the cost function is evaluated.
From the perspective of the representation assumed at host and symbiont populations, individuals of the host population are merely indexing subsets of symbionts from the symbiont population under a variable length chromosome. As such the host population takes the form of a `Genetic Algorithm' that is adapted under a `breeder' style generational framework. There is no particular magic to this decision. That said, given that we are making use of fitness sharing to explicitly maintain diversity at the host population, the initial work utilized crossover as well as mutation by way of the search operators. This turned out to result in premature convergence, particularly in reinforcement style problem domains. Moreover, there is a hidden assumption in the use of crossover -- at least from the perspective of Evolutionary Computation -- whereby parents exchanging material under the crossover metaphor are assumed to be members of the same species. This is relatively easy to establish under biology. However, species identification when competitive models of coevolution such as fitness sharing are employed is a nontrivial problem. Indeed Genetic Algorithms have frequently relied on references to spatial locality to facilitate species identification or diversity (through the application of appropriate distance functions and radii). However, no such concept of distance exists here. Thus, since 2010 we have concentrated on asexual reproduction, thus replying on several forms of mutation as our search operator.
In the case of the symbiont population, the population itself is not of a fixed size. Specifically, symbionts `die' when they are no longer indexed by individuals from the host population. Variation in the symbiont population is achieved through the action of the mutation operator at the host, care of the breeding cycle. Thus, each generation will result in a fixed number of hosts being replaced by new hosts. The hierarchical relationship between host and symbiont populations results in a variable number of symbionts dying/ being borne.
- See Lichodzijewski and Heywood (2010a) for the complete algorithm description.
- See for example Doucette, Lichodzijewski
and Heywood (2009) where an earlier version of the SBB algorithm is applied to classification data sets with up to
100,000 attributes.
- GPTP 2009 slides
- See for example Lichodzijewski and Heywood (2010a) and Zolaktaf (2010).
- With respect to the NIPS 2003 challenge data sets the following results are nominally possible under SBB: balanced detection rate and unique attributes per solution; where x = {A, D, G, M} denote Arcene, Dexter, Gisette and Madelon respectively. A1000 therefore implies results under Arcene without pre-filtering the attribute space, whereas A50 and A300 are two prefilters (reducing the attribute space to 50 and 300 attributes respectively). [All results derived by Alexander Loginov].
Problem decomposition and Hierarchical model building under Evolutionary Policy Search
Generalizing this to a framework for hierarchical model building implies that the hosts previously evolved become candidate symbiont actions for a new layer of host--symbionts, as per the following figure. This results in a very natural metaphor for hierarchical reinforcement learning or layered learning. No a priori decomposition of the problem domain is necessary (although this can naturally be included). The resulting architectures are completely evolved under a single cost function. Archichecturally the Layered SBB framework has the following form:
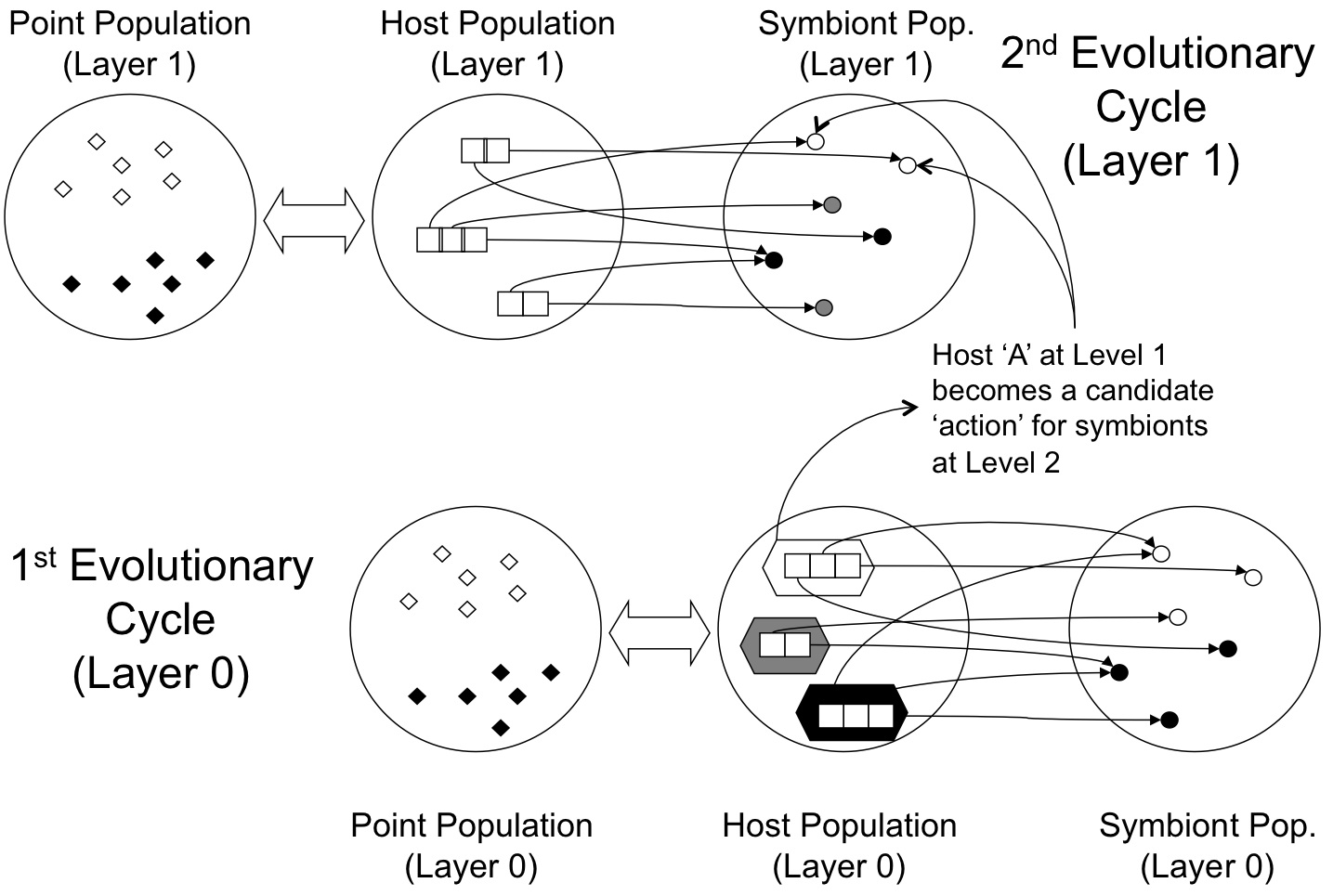
Recent results indicate that the Layered SBB model is particularly effective under reinforcement learning domains.
- See for example Lichodzijewski
and Heywood (2010b) where an initial study is performed under the very challenging domain of the Rubik Cube.
- GPTP 2010 slides
- Tutorial under for truck reversal and Acrobot Handstand task
Real-valued Actions and Future development
One generalization of the basic SBB algorithm enables the algorithm to build regression models. In effect the bidding policy of each symbiont identifies the subset of exemplars on which a regression model is built. Experiments currently under way are considering the case of piece-wise regression, with possible extensions including the use of Temporal Difference methods for providing real-valued control policies.
Future work potentially includes a wide range of issues, a short list of which might look like:- Identification and matching of ecological niches from the point population to subsets of hosts. Given that
hosts are rewarded for their diversity
why should hosts be measured relative to contexts against which they are not adapted? - Identification of limits to the resource allocated to each layer of evolution. An arbitrary number of breeding epochs is currently a priori allocated to each layer for which host evolution takes place. A more satisfactory model would be based on the a measure of adaptiveness demonstrated by a layer. After performance stagnates, a new layer might be initialized.
- Relationships to related work such as Temporal Difference methods for parameter tuning of piece-wise linear models utilized in real-valued SBB or transfer learning in which tasks previously learnt are redeployed under new contexts.