
The objective of this assignment is for you to gain experience in the design and implementation of both parallel shared memory and distributed memory algorithms.
Consider the Selection Problem (also called the ith order statistic) defined as follows:
Input: A set A of n (distinct) numbers and an integer i, with 1 <= n.
Output: The element x in A that is larger than exactly i - 1 other elements of A.
The Selection Problem can be solved using the Randomized-Select Algorithm described in "Introduction to Algorithms" by Cormen, Leiserson, Rivest and Stein and given below.

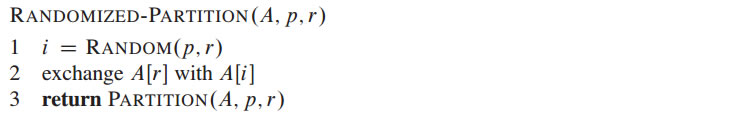

Complete the following algorithm design and programming questions. For the design questions first explain the idea behind your algorithm, then give psuedo-code, and finally analyse the performance asymptotically. For each programming question, implement efficient well commented code and then carefully evaluate its performance.
1. Sequential Randomized Select with Duplicate Elements
Consider the Randomized-Select Algorithm given above. Does the algorithm work when we have duplicate elements? That, is if we slightly change the definition of the output to return the element x in A that is larger or equal to i - 1 other elements of A, can we use the algorithm given above? If not describe carefully what modifications are needed to the algorithm to handle this case. Do your modifications change the time complexity for this sequential method? Submit a write-up of your algorithm with analysis and answers to these questions.
2. Implement Sequential Randomized Select
Create a sequential C implementation of your Randomized-Select Algorithm as you described it in Question 1. Be sure to implement an in-place version that handles duplicates. Test your code by generating an input array A consisting of all the intergers between 1 and a large N stored in random order. Demonstrate that calling Randomized-Select(A, 0, N-1, i) returns i for all 0 < i <= N. How can you demonstrate that it also works when you have duplicates?
Now run a set of timing experiments using CGM6 or CGM7 in which you graph time as a function of N. How close to linear are the resulting runtimes? Submit 1) your well commented code, 2) your testing, and 3) your experimental graphs and commentary.
3. Design a Shared-Memory Algorithm for Randomized Select
Design a shared memory variant of your Randomized-Select Algorithm. You will need to design a parallel version of Partition that runs in O(N/P + P), where N is the number of items and P the number or processors or cores. Your method should be in-place, but if you can't figure out how to make it in place you can make 1 copy of the data for part marks. Submit clear pseudo-code, explanation, and analysis.
4. Implement a Shared-Memory Algorithm for Randomized Select in OpenMP
Implement your algorithm from Question 3 in C and Open-MP. Run the same set of test as in Question 2 to confirm that it is working correctly.
Now run a set of timing experiments using CGM6 or CGM7 in which you 1) graph time as a function of N for P = 16, and 2) graph time as a function of P for P <= 32 where N is a large fixed value. Also graph the associated speedup curve. Submit 1) your well commented code, 2) your testing, and 3) your experimental graphs and commentary.
5. Design a Distributed-Memory Algorithm for Randomized Select
Design a distributed memory variant of your Randomized-Select Algorithm using the CGM model. You will likely need to design a parallel version of Partition that runs in O(N/P + P) local computation time and O(1) collective communication operations, where N is the number of items and P the number of processors. Your method should be in-place and you can assume that the N data items (ie. the array A) starts distributed with N/P items per processor over the parallel machine. Submit clear pseudo-code, explanation, and analysis.
6. Implement a Distributed-Memory Algorithm for Randomized Select using MPI
Implement your algorithm from Question 5 in C and MPI. Run the same set of tests as in Question 2 to confirm that it is working correctly.
Now run a set of timing experiments using ACEnet hardware in which you 1) graph time as a funcation of N for P = 32 (likely 32 cores distrributed over 4 or 8 nodes), and 2) graph time as a function of P for P <= 32, where N is a large fixed value. Also graph the associated speedup curve. You will need a big value of P to see speedup! Submit 1) your well commented code, 2) your testing, and 3) your experimental graphs and comentary. Note your MPI method does not need to also use OpenMP!
Please see parallel_trap.c as an example of how to time your codes.