
 |
Algorithm Improvement through Performance Measurement: Part 7
April 28, 2010
URL:http://www.drdobbs.com/architecture-and-design/parallel-counting-sort/224700144
Algorithm Improvement through Performance Measurement: Part 1
Algorithm Improvement through Performance Measurement: Part 2
Algorithm Improvement through Performance Measurement: Part 3
Algorithm Improvement through Performance Measurement: Part 4
Algorithm Improvement through Performance Measurement: Part 5
Algorithm Improvement through Performance Measurement: Part 6
To date, the focus for this series has been on measurement-based performance optimization of various sorting algorithms, such as Counting Sort, several Radix Sorts, Insertion and Selections Sorts, on a single processor. These implementations, while high-performance through careful use of the hybrid algorithm and data type adaptable approach, use only a portion of the available computational resources. On a quad-core hyper-threaded processor such as the Intel i7 860, these single-threaded algorithms utilize somewhere between 12% and 25% of the processor, leaving 75% to 88% of the compute power idle. As the number of cores increases, following Moore's self-fulfilling prophecy, a higher percentage of the CPU will be unutilized by single-threaded algorithm implementations. In this article and ones to come, the previously developed high-performance serial sorting algorithms will be refactored into parallel algorithms to raise the performance even higher by utilizing multicore computational resources.
Several companies have worked tirelessly to create tools to enable parallel programming. Intel has a vested interest in enabling multicore programming, due to silicon shrinking continuing its path while frequency and power density growth is unable to scale at the same rate. Intel, for instance, has developed Threading Building Blocks and Integrated Performance Primitives (IPP) libraries, along with a powerful suite of compiler, multicore/multi-thread development and performance analysis tools. The Intel C++ compiler supports the latest version of the OpenMP standard, which is one of the parallel programming methods. Intel has also acquired Cilk Arts and the Cilk++ parallel compiler, and is developing Ct Technology.
nVidia has developed CUDA programming environment to enable programs to runs on hundreds of cores in graphics processors (GPUs) across many GPUs, enabling supercomputer level of performance. OpenCL is an industry effort at portable parallel programming across CPUs and graphics processors (GPUs). Sieve C++ Parallel programming system offers a portable environment for many CPUs and game systems. Microsoft Visual Studio 2010 has a suite of tools to enable visualization and debug of parallel applications, as well a Parallel Pattern Library (PPL). These are wonderful developments at simplifying the laborious and complex task of parallel programming. I'll explore some of these exciting tools in this series by applying them to the problem of transforming sorting algorithms from serial to parallel.
The first tool to be explored is Intel's Threading Building Blocks (TBB), a thread-pool management library along with sophisticated templates for C++ parallel programming development. With many parallel constructs and a work-stealing thread scheduler, TBB enables the programmer to focus on the parallel problem instead of the mechanics of thread management. TBB works on several operating systems and has support for a variety of parallel programming patterns. Let's dive right in and apply TBB to the fastest sorting algorithm developed so far -- the Counting Sort.
Counting Sort is a very efficient, in-place, high-performance sorting algorithm that is more than 20X faster than STL sort(). It handles arrays of 8-bit and 16-bit signed and unsigned numbers very well [2]. For arrays of numbers it does not move the array elements, but instead counts the occurrence of each possible value, and then constructs the sorted array from these counts. Counting Sort is a linear-time O(n) algorithm, which performs 2n amount of work -- n for reading/counting, n for writing/constructing.
Listing 1 is an implementation of the Counting Sort algorithm for sorting an array of 8-bit unsigned numbers.
// Copyright(c), Victor J. Duvanenko, 2010
inline void CountingSort( unsigned char* a, unsigned long a_size )
{
if ( a_size < 2 ) return;
const unsigned long numberOfCounts = 256;
// one count for each possible value of an 8-bit element (0-255)
unsigned long count[ numberOfCounts ] = { 0 }; // count array is initialized to zero by the compiler
// Scan the array and count the number of times each value appears
for( unsigned long i = 0; i < a_size; i++ )
count[ a[ i ] ]++;
// Fill the array with the number of 0's that were counted, followed by the number of 1's, and then 2's and so on
unsigned long n = 0;
for( unsigned long i = 0; i < numberOfCounts; i++ )
for( unsigned long j = 0; j < count[ i ]; j++ )
a[ n++ ] = (unsigned char)i;
}
The algorithm creates a count array of 256 elements (32-bits each) -- one for each possible value for an 8-bit number -- and initializes the count array to zero. The first for loop counts the occurrence of each 8-bit value by scanning the array from beginning to end. The second for loop creates the sorted array by storing/writing the counted number of each element. For a detailed explanation of the Count Sort algorithm for arrays of unsigned and signed numbers see Part 6 of this series.
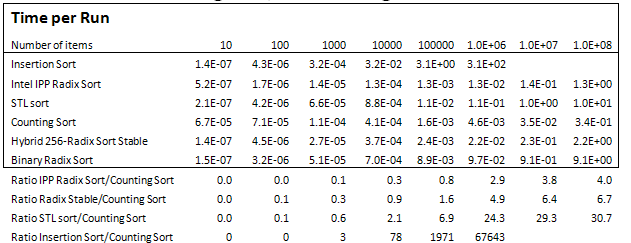
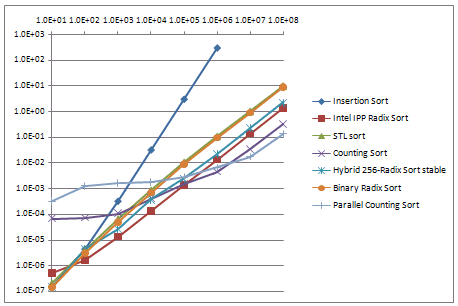
The performance of the initial Parallel Counting Sort implementation is in Table 1 and Figure 1 for arrays of 8-bit unsigned numbers:
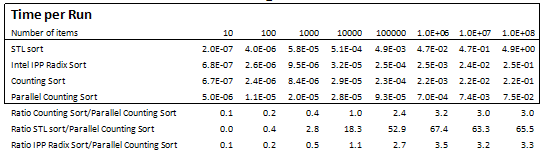
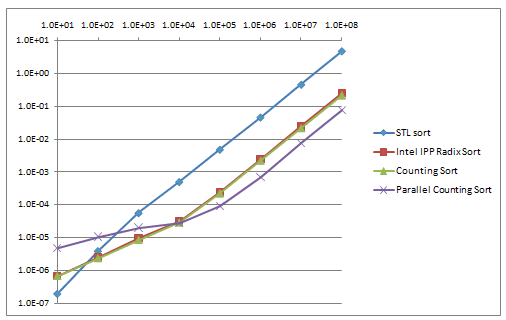
This initial version produced a speedup of up to 3X for large arrays, when running on a quad-core i7 860 CPU with hyper-threading. Parallel Counting Sort is up to 67X faster than STL sort() and 3.3X faster than Intel IPP Radix Sort for medium and large arrays, but is slower for smaller array sizes.
Listing 2 shows the top-level function of the initial Parallel Count Sort implementation. This code looks very similar to the serial implementation shown in Listing 1, except for the initialization of the count array, and the counting for loop.
// Copyright(c), Victor J. Duvanenko, 2010
#include "tbb/tbb.h"
using namespace tbb;
// Listing 2
inline void CountingSort_TBB( unsigned char* a, unsigned long a_size )
{
if ( a_size < 2 ) return;
const unsigned long numberOfCounts = 256;
CountingType count( a ); // contains the count array, which is initialized to all zeros
// Scan the array and count the number of times each value appears
// for( unsigned long i = 0; i < a_size; i++ )
// count[ a[ i ] ]++;
parallel_reduce( blocked_range< unsigned long >( 0, a_size ), count );
// Fill the array with the number of 0's that were counted, followed by the number of 1's, and then 2's and so on
unsigned long n = 0;
for( unsigned long i = 0; i < numberOfCounts; i++ )
for( unsigned long j = 0; j < count.my_count[ i ]; j++, n++ )
a[ n ] = (unsigned char)i;
}
The initialization of the count array has been replaced by a constructor statement CountingType count( a ), which creates a variable of CountingType, and passes the pointer to the input array to its constructor.
The counting for loop has been replaced by the TBB parallel_reduce() function. This function is directed to process the array elements in range of 0 to a_size (i.e., the entire input array) and to use the count variable (which holds the pointer to the input array). The blocked_range is a TBB template class that supports a range capable of recursive splitting. This range includes the beginning elements (0 in our case), but excludes the ending point (a_size). The first argument to the parallel_reduce() function is a constructor for a blocked_range variable.
'Listing 3 shows the CountingType class definition, which contains several methods used by the TBB parallel_reduce() function.
// Copyright(c), Victor J. Duvanenko, 2010
#include "tbb/tbb.h"
using namespace tbb;
class CountingType
{
unsigned char* my_input_array; // a local copy to the array being counted
// to provide a pointer to each parallel task
public:
static const unsigned long numberOfCounts = 256;
unsigned long my_count[ numberOfCounts ]; // the count for this task
CountingType( unsigned char a[] ) : my_input_array( a ) // constructor, which copies the pointer to the array being counted
{
for( unsigned long i = 0; i < numberOfCounts; i++ ) // initialized all counts to zero, since the array may not contain all values
my_count[ i ] = 0;
}
// Method that performs the core work of counting
void operator()( const blocked_range< unsigned long >& r )
{
unsigned char* a = my_input_array; // these local variables are used to help the compiler optimize the code better
size_t end = r.end();
unsigned long* count = my_count;
for( unsigned long i = r.begin(); i != end; ++i )
count[ a[ i ] ]++;
}
// Splitter (splitting constructor) required by the parallel_reduce
// Takes a reference to the original object, and a dummy argument to distinguish this method from a copy constructor
CountingType( CountingType& x, split ) : my_input_array( x.my_input_array )
{
for( unsigned long i = 0; i < numberOfCounts; i++ ) // initialized all counts to zero, since the array may not contain all values
my_count[ i ] = 0;
}
// Join method required by parallel_reduce
// Combines a result from another task into this result
void join( const CountingType& y )
{
for( unsigned long i = 0; i < numberOfCounts; i++ )
my_count[ i ] += y.my_count[ i ];
}
};
The class holds the pointer to the input array and the count array (which is 256 elements -- one element for each possible value of an unsigned 8-bit number). The interface consists of the constructor, which receives the pointer to the input array to be sorted (this pointer is remembered for later use). The constructor also initializes the count array to all zeros. In other words, the CountingType class holds the count[] array and several supporting methods -- it wraps the algorithm in a class that can be passed to a function.
The interface defines several methods that are required by the TBB parallel_reduce() function: the operator(), the splitting constructor, and the join() method. The operator() method implements what the CountingType class does -- the core algorithm. However, a partial range of the input array needs to be handled by this method (from r.begin() to r.end(), but not including r.end()). The body of operator() has a for loop that is very similar to the counting loop of Listing 1.
Parallel_reduce() splits the input array into sub-arrays, which are then processed by each computational core in parallel. To do this efficiently, however, each sub-array needs to have its own independent count[] array that is initialized to zeros and then counts the sub-array elements. In other words, instead of sharing the count[] array among multiple threads, the count[] array is duplicated so that each thread has and operates on its own copy (as illustrated below).
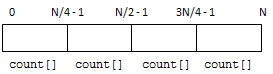
TBB parallel_reduce() recursively splits the input array into P sub-arrays, where P is the number of processors available. During each recursive split, the splitter method is called. After the algorithm completes processing each sub-array, the join method is called, to combine the results from two sub-arrays. This process is illustrated by the diagram below.
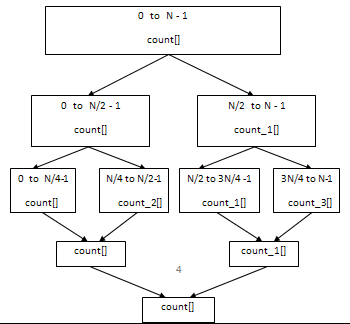
The splitter method, which looks like a copy constructor with a dummy split second argument, creates a copy of CountingType variable by copying the pointer to the input array and initializing the count[] array to zeros. This work is necessary to process a new sub-array independently (as shown in the upper half of the graph above -- note count[] and count_1[] are separate arrays).
Once the sub-arrays have been processed separately, each with their own count[] arrays, the results must be combined into a single count[] array. This combining operation is handled by the join() method, which the TBB parallel_reduce() calls. This is illustrated in the lower half of the diagram above. The join() method combines the count[] array from the CountingType argument passed to it, with its own internal count[] array. At the end, a single count[] array remains, just like the serial version of the algorithm.
Listing 4 shows the initial Parallel Counting Sort implementation for arrays of 16-bit unsigned numbers. The performance is shown in Table 2 and Figure 2.
// Copyright(c), Victor J. Duvanenko, 2010
#include "tbb/tbb.h"
using namespace tbb;
class Counting16Type
{
unsigned short* my_input_array; // a local copy to the array being counted
// to provide a pointer to each parallel task
public:
static const unsigned long numberOfCounts = 256 * 256;
unsigned long my_count[ numberOfCounts ]; // the count for this task
Counting16Type( unsigned short a[] ) : my_input_array( a ) // constructor, which copies the pointer to the array being counted
{
for( unsigned long i = 0; i < numberOfCounts; i++ ) // initialized all counts to zero, since the array may not contain all values
my_count[ i ] = 0;
}
// Method that performs the core work of counting
void operator()( const blocked_range< unsigned long >& r )
{
unsigned short* a = my_input_array; // these local variables are used to help the compiler optimize the code better
size_t end = r.end();
unsigned long* count = my_count;
for( unsigned long i = r.begin(); i != end; ++i )
count[ a[ i ] ]++;
}
// Splitter (splitting constructor) required by the parallel_reduce
// Takes a reference to the original object, and a dummy argument to distinguish this method from a copy constructor
Counting16Type( Counting16Type& x, split ) : my_input_array( x.my_input_array )
{
for( unsigned long i = 0; i < numberOfCounts; i++ ) // initialized all counts to zero, since the array may not contain all values
my_count[ i ] = 0;
}
// Join method required by parallel_reduce
// Combines a result from another task into this result
void join( const Counting16Type& y )
{
for( unsigned long i = 0; i < numberOfCounts; i++ )
my_count[ i ] += y.my_count[ i ];
}
};
inline void CountingSort_TBB( unsigned short* a, unsigned long a_size )
{
if ( a_size < 2 ) return;
const unsigned long numberOfCounts = 256 * 256;
Counting16Type count( a ); // contains the count array, which is initialized to all zeros
// Scan the array and count the number of times each value appears
// for( unsigned long i = 0; i < a_size; i++ )
// count[ a[ i ] ]++;
parallel_reduce( blocked_range< unsigned long >( 0, a_size ), count );
// Fill the array with the number of 0's that were counted, followed by the number of 1's, and then 2's and so on
unsigned long n = 0;
for( unsigned long i = 0; i < numberOfCounts; i++ )
for( unsigned long j = 0; j < count.my_count[ i ]; j++, n++ )
a[ n ] = (unsigned short)i;
}
The initial 16-bit unsigned Parallel Counting Sort implementation produced an algorithm that is up to 77X faster than STL sort() for large array sizes, is up to 10X faster than Intel's IPP Radix Sort for the larger array sizes, and is up to 2.5X faster than serial Counting Sort but only for the largest array sizes. This implementation performs inferior to all other algorithms for the smaller array sizes and to the serial Counting Sort for mid-size arrays. A hybrid algorithm implementation could be easily created to produce a high performing algorithm for all array sizes, as was done in previous articles of this series.
The Counting Sort algorithm has substantial parallelism inherently within several areas. Initialization of the count array (256 elements for 8-bit and 64K elements for 16-bit) could be performed entirely in parallel, if this was possible. This operation is similar to a reset signal assertion in hardware, where all flip-flops are cleared simultaneously. Thus, for an 8-bit algorithm up to 256 initializations can be performed in parallel, whereas for 16-bit algorithm up to 64K initializations can be performed in parallel.
The counting portion of the algorithm has substantial inherent parallelism, where the input array can be split into many small portions, which are counted independently of others. These counts can then be combined. Of course, the overhead of splitting and joining limits the performance gains.
The writing portion of the algorithm also has substantial inherent parallelism. In the limit each output array element could be written in parallel, independent of all other array elements. This would require independent/parallel access to the count[] array and to the output array, which is currently not practical.
The first venture into parallel programming through the implementation of the Parallel Counting Sort algorithm proved to be rewarding. Leveraging the efforts of Intel's TBB team, the move into parallel computing is significantly simplified and accelerated, along with impressive performance results. However, using TBB requires C++ expertise along with many examples and thorough documentation to demonstrate and explain concepts and usage. Intel TBB accomplishes both of these things well, along with implementing a variety of core parallel computing patterns. By using templates, TBB fits easily and seamlessly into the C++ development environments on many platforms.
The speedups obtained for arrays of 8-bit unsigned numbers were about 3X, and over 2X for arrays of unsigned 16-bit numbers, using a quad-core processor. This demonstrated that Counting Sort, while performing very little work per array element, has inherent parallelism which can be harnessed through parallel processing. Only a portion of the overall algorithm was refactored to a parallel implementation, the initialization and the counting portions, while writing of the results into the array remained non-parallel for now.
16-bit Counting Sort showed performance issues at small and mid-size arrays, which will be investigated and improved in future articles. This article is just the beginning of the journey into parallel computing. Intel TBB provides many other mechanisms and patterns necessary to support high-performance parallel computation, which will be explored in future articles. Other tools briefly described provide similar functionality with the goal of enabling software migration to take advantage of expanding hardware parallel processing.
Terms of Service | Privacy Statement | Copyright © 2012 UBM Tech, All rights reserved.