Due: March 4th by 11:59pm

Geometric primitives. To get started, implement a geometric primitive for axis-aligned rectangles in the plane.

You can either use data type Point2D.java for points in the plane, which implements a superset of the following API, or create your own:

public class Point2D implements Comparable<Point2D> {
   public Point2D(double x, double y)              // construct the point (x, y)
   public double x()                               // x-coordinate
   public double y()                               // y-coordinate
   public double distanceTo(Point2D that)          // Euclidean distance between two points
   public double distanceSquaredTo(Point2D that)   // square of Euclidean distance between two points
   public int compareTo(Point2D that)              // for use in an ordered symbol table
   public boolean equals(Object that)              // does this point equal that?
   public String toString()                        // string representation
}

public class RectHV {
   public RectHV(double xmin, double ymin,         // construct the rectangle [xmin, xmax] x [ymin, ymax]
                 double xmax, double ymax)         // throw an exception if (xmin > xmax) or (ymin > ymax)
   public double xmin()                            // minimum x-coordinate of rectangle
   public double ymin()                            // minimum y-coordinate of rectangle
   public double xmax()                            // maximum x-coordinate of rectangle
   public double ymax()                            // maximum y-coordinate of rectangle
   public boolean contains(Point2D p)              // does this rectangle contain the point p (either inside or on boundary)?
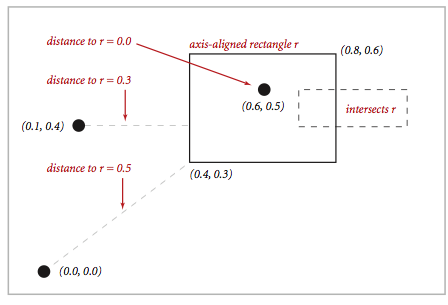
   public boolean intersects(RectHV that)          // does this rectangle intersect that rectangle (at one or more points)?
   public double distanceTo(Point2D p)             // Euclidean distance from point p to the closest point in rectangle
   public double distanceSquaredTo(Point2D p)      // square of Euclidean distance from point p to closest point in rectangle
   public boolean equals(Object that)              // does this rectangle equal that?
   public String toString()                        // string representation
}

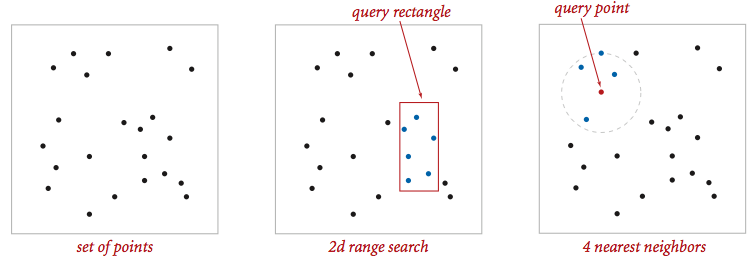
Brute-force implementation. Write a data type PointSET.java that represents a set of points in the unit square. Implement the following API by using a binary search tree (using either SET or java.util.TreeSet) or a sequence..

public class PointSET {
   public PointSET()                               // construct an empty set of points
   public boolean isEmpty()                        // is the set empty?
   public int size()                               // number of points in the set
   public void insert(Point2D p)                   // add the point p to the set 
   public boolean contains(Point2D p)              // does the set contain the point p?
   public Collection<Point2D> range(RectHV rect)     // all points in the set that are inside the rectangle
   public Point2D nearest(Point2D p)               // a nearest neighbor in the set to p; null if set is empty
}

2d-tree implementation. Write a data type KdTree.java that uses a 2d-tree to implements the same API as PointSET. A 2d-tree is a generalization of a binary search tree to two-dimensional keys. The idea is to build a binary search tree with points in the nodes, using the x- and y-coordinates of the points as keys in strictly alternating sequence.

• Search and insert. The algorithms for search and insert are similar to those for BSTs, but at the root we use the x-coordinate (if the point to be inserted has a smaller x-coordinate than the point at the root, go left; otherwise go right); then at the next level, we use the y-coordinate (if the point to be inserted has a smaller y-coordinate than the point in the node, go left; otherwise go right); then at the next level the x-coordinate, and so forth.

insert (0.7, 0.2)	insert (0.5, 0.4)	insert (0.2, 0.3)	insert (0.4, 0.7)	insert (0.9, 0.6)

The prime advantage of a 2d-tree over a BST is that it supports efficient implementation of range search and nearest neighbor search. Each node corresponds to an axis-aligned rectangle in the unit square, which encloses all of the points in its subtree. The root corresponds to the unit square; the left and right children of the root corresponds to the two rectangles split by the x-coordinate of the point at the root; and so forth.

• Range search. To find all points contained in a given query rectangle, start at the root and recursively search for points in both subtrees using the following pruning rule: if the query rectangle does not intersect the rectangle corresponding to a node, there is no need to explore that node (or its subtrees). A subtree is searched only if it might contain a point contained in the query rectangle.
• Nearest neighbor search. To find a closest point to a given query point, start at the root and recursively search in both subtrees using the following pruning rule: if the closest point discovered so far is closer than the distance between the query point and the rectangle corresponding to a node, there is no need to explore that node (or its subtrees). A subtree is searched only if it might contain a point that is closer than the best one found so far. The effectiveness of the pruning strategy depends on quickly finding a nearby point. To do this, organize your recursive method so that it begins by moving down the 2d-tree by considering the same sequence of nodes that would be considered if you were inserting the query point.

Analysis.  Analyze your approach to this problem giving estimates of its time and space requirements. In particular:

• Give the total memory usage in bytes of your 2d-tree data structure as a function of the number of points N. Count all memory that is used by your 2d-tree, including memory for the nodes, points, and rectangles.
• Give the worse case running time to build a 2d-tree on N random points in the unit square. (Do not count the time to read in the points from standard input.)
• How many nearest neighbor calculations can your 2d-tree implementation perform per second for input100K.txt (100,000 points) and input1M.txt (1 million points), where the query points are random points in the unit square? (Do not count the time to read in the points or to build the 2d-tree.) Repeat this question but with the brute-force implementation.

Submission.  Submit RectHV.java, PointSET.java, and KdTree.java and any other files needed by your program.